
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интегралы уравнения движения
|
|
|
|
Известны следующие важные частные случаи, когда уравнение (4.4) может быть проинтегрировано: а) движение потенциальное, б) движение установившееся.
Используя соотношение векторного анализ  , уравнение движения можно представить в виде (в форме Громеки-Лэмба)
, уравнение движения можно представить в виде (в форме Громеки-Лэмба)
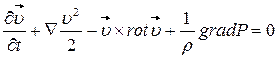 (4.10)
(4.10)
Введем функцию  .
.
При неустановившемся безвихревом движении 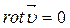 ,
, 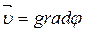 . Тогда
. Тогда
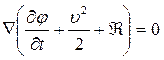
или
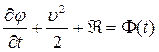 (4.11)
(4.11)
Выражение (4.11) известно под названием интеграла Лагранжа-Коши.
В случае установившегося движения из уравнения (4.10) следует:
 (4.12)
(4.12)
Если при установившемся движении 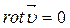 или рассматриваются случаи движения вдоль линии тока или вдоль вихревой линии, когда
или рассматриваются случаи движения вдоль линии тока или вдоль вихревой линии, когда 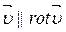 , векторное произведение
, векторное произведение  . При этом
. При этом
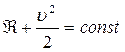 (4.13)
(4.13)
Выражение (4.13) известно под названием интеграла Бернулли.
Ввиду важных в практическом отношении приложений интеграла Бернулли, ниже приводятся его некоторые известные формы.
Принимая во внимание, что изэнтропическое движение идеального газа отвечает условию 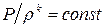 , функцию
, функцию  можно представить в виде
можно представить в виде
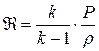 (4.14)
(4.14)
Учитывая, что скорость звука в идеальном газе  , интеграл (4.13) приводится к виду
, интеграл (4.13) приводится к виду
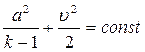 (4.15)
(4.15)
Представляет интерес оценка давления «заторможенного» потока газа. Искомое давление нетрудно найти, используя интеграл (4.15). Представим его в виде
 (4.16)
(4.16)
Здесь через 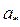 обозначено значение скорости звука в той точке, где скорость газа равна нулю.
обозначено значение скорости звука в той точке, где скорость газа равна нулю.
Принимая во внимание, что  , уравнение (4.16) преобразуется к виду
, уравнение (4.16) преобразуется к виду
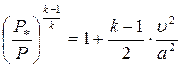 (4.17)
(4.17)
или
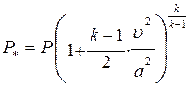 (4.18)
(4.18)
§ 4.4. Одномерное изэнтропическое движение гaза. Инварианты Римана
Одномерное неустановившееся течение газа – наиболее простой случай движения. Тем не менее, он позволяет выяснить ряд физических закономерностей неустановившихся движений.
Рассматриваемое движение газа определяется системой уравнений (4.9). В случае движения с плоской симметрией она дополнительно упрощается:
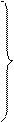
 , (4.19)
, (4.19)
где 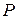 ,
, 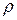 ,
, 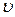 - давление, плотность и массовая скорость газа.
- давление, плотность и массовая скорость газа.
Следуя К.П. Станюковичу, приведем систему (4.19) к более удобному для последующих исследований виду [2].
Согласно (4.14) функция 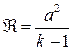 , следовательно,
, следовательно,
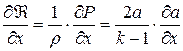
Кроме того, так как при изэнтропическом движении  =
=  , то
, то 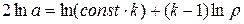 или
или 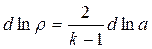 .
.
Подставляя значения 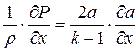 ,
, 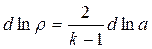 соответственно в первое и второе уравнения системы (4.19), домножая второе уравнение почленно на «
соответственно в первое и второе уравнения системы (4.19), домножая второе уравнение почленно на «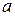 », получаем:
», получаем:
 (4.20)
(4.20)
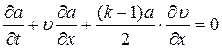 (4.21)
(4.21)
Данная система уравнений замыкается адиабатой Пуассона 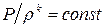 .
.
Решение системы уравнений (4.20), (4.21) приведено в [2]. Ниже рассматривается решение этой системы в изложении Ю.С. Яковлева [4].
Системы дифференциальных уравнений в частных производных обычно решаются с помощью метода характеристик.
|
 Пусть в плоскости
Пусть в плоскости 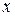 ,
, 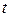 задана кривая «
задана кривая «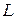 », рис. 24, и на этой кривой
», рис. 24, и на этой кривой 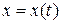 известны функции
известны функции  ,
,  . Необходимо найти интегралы (решения) системы (4.20)-(4.21), которые на кривой
. Необходимо найти интегралы (решения) системы (4.20)-(4.21), которые на кривой 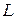 обращались бы в заданные значения. Иначе говоря, необходимо найти интегральную поверхность, удовлетворяющую рассматриваемой системе уравнений и проходящей через кривую
обращались бы в заданные значения. Иначе говоря, необходимо найти интегральную поверхность, удовлетворяющую рассматриваемой системе уравнений и проходящей через кривую 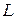 (задача Коши).
(задача Коши).
 ;
; 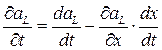
в исследуемые уравнения:

 (4.22)
(4.22)
Остановимся на определении 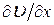 ,
, 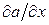 . Имеем
. Имеем
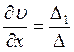 ;
; 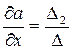 ,
,
где 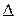 ,
,  ,
, 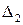 - соответствующие определители системы (4.22).
- соответствующие определители системы (4.22).
В процессе оценки величин  ,
, 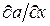 возможны следующие основные случаи:
возможны следующие основные случаи:
1. 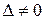 ,
, 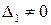 ,
, 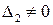
2.  ,
, 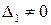 ,
, 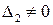
3.  ,
,  ,
, 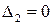 .
.
В первом случае имеется место вполне определенное значение производных в точке  и в ее окрестности вдоль кривой «
и в ее окрестности вдоль кривой «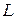 ». Задача Коши имеет единственное решение.
». Задача Коши имеет единственное решение.
Во втором случае значения производных бесконечны. Кривую «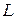 » в окрестности точки
» в окрестности точки  называют линией разрыва.
называют линией разрыва.
В третьем случае существует бесчисленное множество значений производных  ,
, 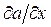 , отвечающих рассматриваемой системе. Задача Коши не имеет единственного решения. Направление касательной к кривой «
, отвечающих рассматриваемой системе. Задача Коши не имеет единственного решения. Направление касательной к кривой «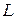 » в точке
» в точке  называют характеристическим направлением.
называют характеристическим направлением.
Кривую «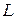 », в каждой точке которой направление касательной отвечает характеристическому направлению, называют характеристикой. Известно, что решение уравнений характеристик эквивалентно решению исходной системы уравнений.
», в каждой точке которой направление касательной отвечает характеристическому направлению, называют характеристикой. Известно, что решение уравнений характеристик эквивалентно решению исходной системы уравнений.
Уравнения характеристик системы (4.22) можно записать, приравняв нулю определители 
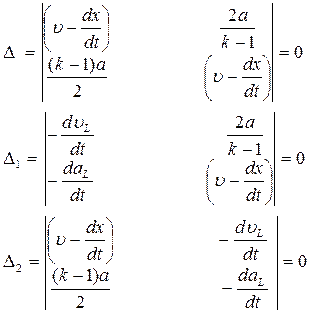 (4.23)
(4.23)
Раскрыв определитель 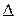 , получаем
, получаем
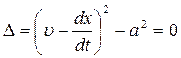
Видно, что этот определитель обращается в ноль в следующих случаях:

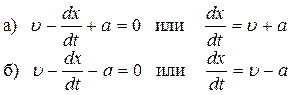 (4.24)
(4.24)
Из уравнений (4.24) следует, что характеристики распространяются со звуковой скоростью.
Рассмотрим определитель 

При 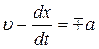 получаем соответственно:
получаем соответственно:
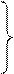
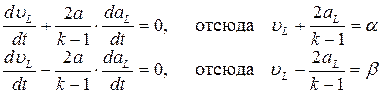 (4.25)
(4.25)
Необходимо отметить, что соотношение 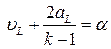 выполняется на характеристике
выполняется на характеристике 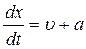 , соотношение
, соотношение 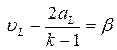 - на характеристике
- на характеристике 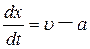 .
.
Равенство нулю определителя 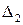 приводит к соотношения, аналогичным (4.25).
приводит к соотношения, аналогичным (4.25).
Так как на кривой L значения 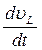 =
=  ,
,  =
= 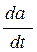 , принято называть характеристикой первого семейства и условиями на этой характеристике соответственно соотношения:
, принято называть характеристикой первого семейства и условиями на этой характеристике соответственно соотношения:
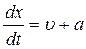 (4.26)
(4.26)
 (4.27)
(4.27)
Аналогично характеристикой второго семейства и условиями на характеристике называют соотношения:
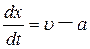 (4.28)
(4.28)
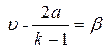 (4.29)
(4.29)
Следует отметить, что соотношения (4.27), (4.29) можно получить другим способом.
Умножая уравнение (4.20) на сомножитель 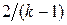 , вычитая и складывая затем полученное уравнение с уравнением (4.21), получаем:
, вычитая и складывая затем полученное уравнение с уравнением (4.21), получаем:

 (4.30)
(4.30)
Возможным решением первого уравнения будет 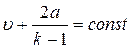 , второго
, второго  .
.
Кратко о физике процессов, описываемых соотношениями (4.26)-(4.29). Видно, что согласно (4.26), (4.27) состояние среды, определяемое величиной  , распространяется в виде волнового возмущения со скоростью
, распространяется в виде волнового возмущения со скоростью 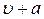 в положительном направлении оси
в положительном направлении оси 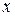 по течению среды, а состояние, определяемое согласно (4.28), (4.29) величиной
по течению среды, а состояние, определяемое согласно (4.28), (4.29) величиной  , распространяется со скоростью
, распространяется со скоростью 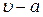 против течения среды. При этом распространение возмущений при дозвуковой скорости будет происходить как в положительном, так и отрицательном направлении по оси
против течения среды. При этом распространение возмущений при дозвуковой скорости будет происходить как в положительном, так и отрицательном направлении по оси 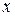 , при сверхзвуковой скорости возмущения будут сноситься течением, и распространение их будет происходить только в положительном направлении оси
, при сверхзвуковой скорости возмущения будут сноситься течением, и распространение их будет происходить только в положительном направлении оси 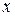 . Волны одного направления, проходя через волны другого направления, будут взаимодействовать и, следовательно, распространение волн противоположных направлений в общем случае не будет независимым.
. Волны одного направления, проходя через волны другого направления, будут взаимодействовать и, следовательно, распространение волн противоположных направлений в общем случае не будет независимым.
Со скоростью звука в среде распространяются малые возмущения. Они могут распространяться в виде волн сжатия и волн разрежения. Волнами сжатия называются такие движения среды, когда при движении каждого элемента среды давление в нем возрастает. Наоборот, когда в процессе движения в каждом элементе среды давление падает, имеют место волны разрежения.
Особые решения уравнений (4.19) (или (4.20)-(4.21)). Пусть движение таково, что вдоль одной из характеристик (например, 1-го семейства) в плоскости 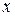 ,
, 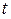 величины скорости
величины скорости 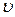 и скорости звука
и скорости звука 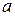 сохраняют постоянное значение. Согласно (4.26) такая характеристика будет прямой, так как на ней
сохраняют постоянное значение. Согласно (4.26) такая характеристика будет прямой, так как на ней  . Обазначим эту характеристику АВ.
. Обазначим эту характеристику АВ.
Рассмотрим далее характеристики 2-го семейства 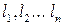 . Пусть они пересекают рассматриваемую характеристику первого семейства
. Пусть они пересекают рассматриваемую характеристику первого семейства  в точках
в точках 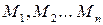 . Для данных характеристик справедливо соотношение
. Для данных характеристик справедливо соотношение
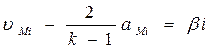 , 1 < I < n (4.31)
, 1 < I < n (4.31)
|
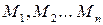 величины
величины 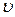 и a одинаковы. Следовательно, постоянными будут и числа
и a одинаковы. Следовательно, постоянными будут и числа  . Таким образом, соотношение
. Таким образом, соотношение 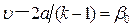 будет выполняться не только вдоль заданной характеристики, но и во всей области.
будет выполняться не только вдоль заданной характеристики, но и во всей области.
Следует отметить, что в рассматриваемом случае не только характеристика 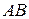 будет прямолинейна в плоскости
будет прямолинейна в плоскости 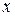 ,
, 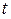 , но и другие характеристики 1-го семейства будут прямыми. Действительно, вдоль каждой такой характеристики согласно (4.27)
, но и другие характеристики 1-го семейства будут прямыми. Действительно, вдоль каждой такой характеристики согласно (4.27)  (на каждой свое
(на каждой свое 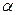 ), но, кроме того, во всей области выполняется
), но, кроме того, во всей области выполняется  . Таким образом, величины
. Таким образом, величины 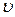 и
и 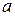 на характеристиках первого семейства будут связаны двумя алгебраическими соотношениями. Отсюда вследствие (4.26) и вытекает справедливость данного утверждения.
на характеристиках первого семейства будут связаны двумя алгебраическими соотношениями. Отсюда вследствие (4.26) и вытекает справедливость данного утверждения.
Вернемся к интегрированию системы уравнений (4.20), (4.21). Вычислив из соотношения  величину
величину 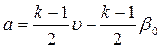 и подставив ее в (4.21), находим
и подставив ее в (4.21), находим
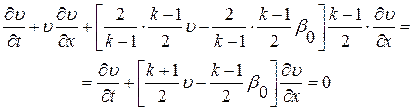 (4.32)
(4.32)
Это линейное дифференциальное уравнение первого порядка эквивалентно следующей системе обыкновенных дифференциальных уравнений:
 (4.33)
(4.33)
Отсюда
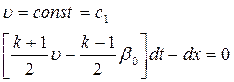
или

Полагая  , находим
, находим
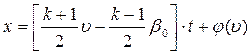 (4.34)
(4.34)
И, кроме того,
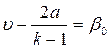 (4.35)
(4.35)
Предположив аналогично, что на характеристике второго семейства величины скоростей частиц газа и скорости звука сохраняют постоянное значение, можно получить:
 (4.36)
(4.36)
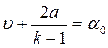 (4.37)
(4.37)
Подставляя в соотношения (4.34), (4.36) значения 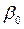 и
и  из (4.35) м (4.37), можно получить:
из (4.35) м (4.37), можно получить:
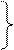
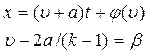 (4.38)
(4.38)
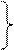
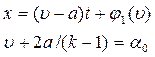 (4.39)
(4.39)
Решение (4.38), (4.39) получено Риманом [2]. При этом решение (4.38) называется прямой волной одного направления, а решение (4.39) - обратной волной одного направления.
Если система координат выбрана так, что положительное направление оси х совпадает с направлением движения волны, то ее движение описывается соотношениями (4.38), а если волна бежит в обратном направлении, то пользуются соотношениями (4.39).
Отдельно следует отметить, что вторые соотношения решения (4.38) и (4.39) называются инвариантами Римана.
Известно, что общие решения двух дифференциальных уравнений в частных производных должны зависеть от двух произвольных функций. Полученные решения, зависящие от одной произвольной функции, представляют собой особые решения. Важным свойством решений (4.38), (4.39) является то обстоятельство, что движения, характеризуемые прямой и обратной волнами одного направления, могут сопрягаться с областью покоя или, в более общем случае, - с областью установившегося движения среды.
Соотношения (4.38), (4.39) используются при решении целого ряда задач.
Пусть, например, в трубе находится газ, подчиняющийся адиабате Пуассона 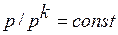 и ограниченный слева поршнем. В некоторый момент времени поршень начинает выдвигаться (двигаться справа налево), причем в начальный момент времени скорость поршня равна нулю, газ находится в покое. Требуется исследовать движение газа.
и ограниченный слева поршнем. В некоторый момент времени поршень начинает выдвигаться (двигаться справа налево), причем в начальный момент времени скорость поршня равна нулю, газ находится в покое. Требуется исследовать движение газа.
Поместим начало системы координат в точку, отвечающую положению поршня в момент покоя; ось 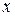 направим вправо. При выдвижении поршня образуется волна разрежения, распространяющаяся по газу в положительном направлении оси
направим вправо. При выдвижении поршня образуется волна разрежения, распространяющаяся по газу в положительном направлении оси 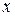 . Состояние покоя в начальный момент времени означает, что
. Состояние покоя в начальный момент времени означает, что 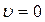 , скорость звука
, скорость звука  . Следовательно, в плоскости
. Следовательно, в плоскости 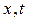 характеристики первого семейства будут прямолинейны, рис 25. Характеристикой, отделяющей невозмущенную среду от области движения, является
характеристики первого семейства будут прямолинейны, рис 25. Характеристикой, отделяющей невозмущенную среду от области движения, является

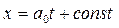
При этом 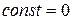 , так как при
, так как при  величина
величина 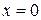 .
.
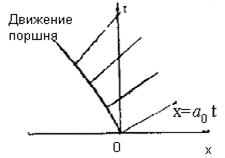

Рис. 25. Семейство характеристик Рис. 26. Семейство характеристик
волны разрежения волны сжатия
Рассматриваемому случаю отвечает особое решение (4.38)
 ,
,
где 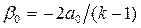 (из условия на характеристике, отделяющей невозмущенную среду и область движения).
(из условия на характеристике, отделяющей невозмущенную среду и область движения).
Отсюда
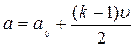 (4.40)
(4.40)
Функция 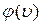 находится с помощью закона движения поршня. При движении поршня каждое его элементарное смещение порождает элементарное волновое возмущение разрежения, которое распространяется со скоростью
находится с помощью закона движения поршня. При движении поршня каждое его элементарное смещение порождает элементарное волновое возмущение разрежения, которое распространяется со скоростью 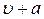 , причем вектор
, причем вектор  направлен по ходу движения поршня.
направлен по ходу движения поршня.
Представленные на рис. 25. характеристики 1-го семейства могут быть записаны в виде
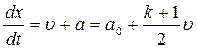 (4.41)
(4.41)
В качестве величины  на каждой из характеристик (4.41) можно взять скорость поршня
на каждой из характеристик (4.41) можно взять скорость поршня  , то есть
, то есть  . В этом случае
. В этом случае  =
= 
 . Для каждого фиксированного значения
. Для каждого фиксированного значения 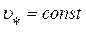 данное соотношение определяет прямую линию в плоскости
данное соотношение определяет прямую линию в плоскости 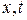 . При этом, чем больше величина
. При этом, чем больше величина  , тем меньше скорость распространения возмущений, так как
, тем меньше скорость распространения возмущений, так как  , и в плоскости
, и в плоскости 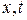 получается веер расходящихся характеристик.
получается веер расходящихся характеристик.
По мере увеличения скорости поршня  разрежение за ним увеличивается и соответственно уменьшается скорость звука
разрежение за ним увеличивается и соответственно уменьшается скорость звука 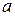 , так как
, так как 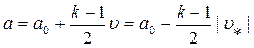 . Если
. Если  , то
, то  . В этот момент за поршнем образуется вакуум (
. В этот момент за поршнем образуется вакуум ( ). Следовательно, при скорости поршня
). Следовательно, при скорости поршня 
 поршень отрывается от газа и никак уже не влияет на его движение - происходит «разлет газа в пустоту».
поршень отрывается от газа и никак уже не влияет на его движение - происходит «разлет газа в пустоту».
Пусть, наоборот, поршень ускоренно вдвигается в трубу, рис.26. При выбранной системе координат движение газа также описывается решением (4.38).
При таком движении каждое элементарное смещение поршня порождает элементарное волновое возмущение сжатия, которое распространяется слева направо со скоростью 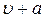 . При этом каждая последующая элементарная волна будет распространяться по более сжатому предыдущей волной газу, вследствие чего амплитуда волны будет возрастать.
. При этом каждая последующая элементарная волна будет распространяться по более сжатому предыдущей волной газу, вследствие чего амплитуда волны будет возрастать.
В отличие от случая выдвижения поршня здесь 
 и, следовательно,
и, следовательно, 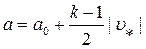 ,
, 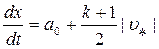 . Видно, чем больше
. Видно, чем больше  , тем больше величина скорости распространения возмущений
, тем больше величина скорости распространения возмущений 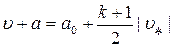 . Поэтому в плоскости
. Поэтому в плоскости 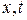 получается веер сходящихся характеристик, которые, в конце концов, пересекутся, рис. 26.
получается веер сходящихся характеристик, которые, в конце концов, пересекутся, рис. 26.
Сходящийся пучок характеристик указывает на тенденцию формирования качественно нового физического процесса – ударной волны (поскольку вдоль каждой из них скорость остается постоянной, а в точке пересечения будет иметь место многозначная функция 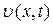 ). Условия возникновения ударных волн рассматриваются в следующем параграфе.
). Условия возникновения ударных волн рассматриваются в следующем параграфе.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 704; Нарушение авторских прав?; Мы поможем в написании вашей работы!
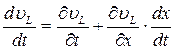
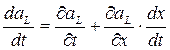 Установим ограничения, накладываемые на рассматриваемую систему вследствие того, что на кривой «
Установим ограничения, накладываемые на рассматриваемую систему вследствие того, что на кривой «