
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Начальные параметры ударной волны при взрывах газовоздушных смесей и конденсированных взрывчатых веществ в атмосфере
|
|
|
|
При взрыве в воздухе в момент выхода детонационной волны на границу облака газовоздушной смеси или поверхность заряда конденсированного ВВ происходит формирование следующей волновой системы: 1-фронта воздушной ударной волны, 2 - поверхности, разделяющей движущийся за фронтом ударной волны воздух и продукты взрыва, 3 – волны разрежения, понижающей давление в продуктах взрыва, рис. 32.
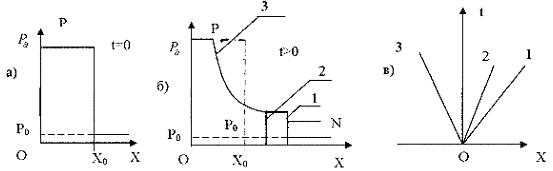 Рис. 32. Формирование волновой системы при выходе детонационной волны на поверхность заряда
Рис. 32. Формирование волновой системы при выходе детонационной волны на поверхность заряда
а - момент выхода детонационной волны на поверхность
заряда (t=0),
б - формирование поверхностей 1, 2, 3 (при t>0),
в - положение поверхностей 1,2 3 в плоскости x, t
На рис.32 обозначено: P0 - давление в невозмущенной атмосфере, 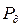 - давление в продуктах взрыва, N - скорость фронта воздушной ударной волны, X 0- граница раздела сред (радиус заряда или средний радиус облака ГВС).
- давление в продуктах взрыва, N - скорость фронта воздушной ударной волны, X 0- граница раздела сред (радиус заряда или средний радиус облака ГВС).
Как отмечалось в §4.1, в газодинамике принято называть: поверхность 1 – поверхность сильного нестационарного разрыва, 2 – поверхность сильного стационарного разрыва, 3 – поверхность слабого разрыва. На поверхности 1 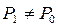 ,
, 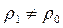 ,
, 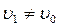 , где индексом “0 “ при давлении P, плотности
, где индексом “0 “ при давлении P, плотности 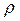 , скорости
, скорости 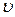 обозначены параметры среды перед фронтом воздушной ударной волны, индексом “1 “ – за фронтом. На поверхности 2 имеют место соотношения: P2= P3,
обозначены параметры среды перед фронтом воздушной ударной волны, индексом “1 “ – за фронтом. На поверхности 2 имеют место соотношения: P2= P3, 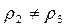 ,
, 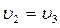 , где аналогично индексом “2 “ обозначены параметры среды перед поверхностью сильного стационарного разрыва, индексом “3 “ – за ней. При этом направление движения воздуха и продуктов взрыва за поверхностями 1 и 2 совпадает с направлением движения данных поверхностей, направление движения продуктов взрыва за поверхностью 3 противоположно направлению ее распространения.
, где аналогично индексом “2 “ обозначены параметры среды перед поверхностью сильного стационарного разрыва, индексом “3 “ – за ней. При этом направление движения воздуха и продуктов взрыва за поверхностями 1 и 2 совпадает с направлением движения данных поверхностей, направление движения продуктов взрыва за поверхностью 3 противоположно направлению ее распространения.
В начальные моменты времени имеют место: P1=P2=P3, 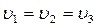 . Данное обстоятельство позволяет, используя известные газодинамические соотношения, определить начальное давление во фронте воздушной ударной волны P1 через величину скорости
. Данное обстоятельство позволяет, используя известные газодинамические соотношения, определить начальное давление во фронте воздушной ударной волны P1 через величину скорости 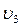 , равную сумме
, равную сумме 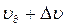 , где значение скорости продуктов взрыва за фронтом детонационной волны
, где значение скорости продуктов взрыва за фронтом детонационной волны 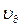 находится по третьему соотношению (4.75), а величина
находится по третьему соотношению (4.75), а величина 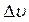 - это дополнительная скорость, сообщаемая продуктам взрыва волной разрежения. Для ее определения обратимся к рис.32 в.
- это дополнительная скорость, сообщаемая продуктам взрыва волной разрежения. Для ее определения обратимся к рис.32 в.
Поверхность 3 – это характеристика. При выбранной системе координат, когда поверхности 1 и 2 движутся в положительном направлении оси X, а поверхность 3 - в противоположном направлении, она определяет обратную волну одного направления (4.39). На поверхности 3 и в области за ней имеет место инвариант Римана
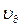 +
+ 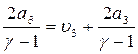 или
или 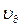 +
+ 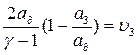 ,
,
то есть
|
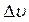 =
= 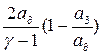
|
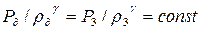 ,
, 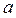 =
= 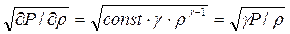 . Тогда
. Тогда 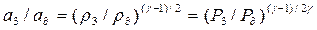 . Используя соотношения (4.75), (4.76), находим
. Используя соотношения (4.75), (4.76), находим 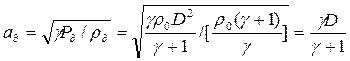 . Следовательно,
. Следовательно, 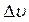 =
= 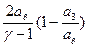 =
= 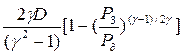
Как отмечалось выше, в начальные моменты времени P3=P2=P1, 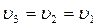 . Обозначим P1=Pф,
. Обозначим P1=Pф, 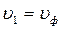 . Согласно (4.50) и (4.54)
. Согласно (4.50) и (4.54) 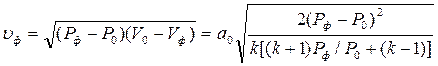 .
.
Подставляя значения 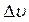 ,
, 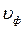 в соотношение
в соотношение 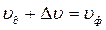 , учитывая, что согласно третьему соотношению (4.75), величина
, учитывая, что согласно третьему соотношению (4.75), величина 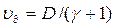 , получаем
, получаем
|
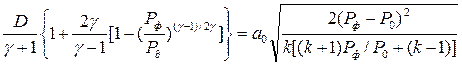 ,
,
где 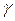 - показатель адиабаты продуктов взрыва;
- показатель адиабаты продуктов взрыва;
k - показатель адиабаты воздуха.
Уравнение (4.81) однозначно определяет начальное значение Pф при взрыве газовоздушных смесей.
При взрыве конденсированных взрывчатых веществ давление детонации составляет 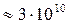 Па. В связи с тем, что при расширении продуктов взрыва в широком диапазоне изменения давления от
Па. В связи с тем, что при расширении продуктов взрыва в широком диапазоне изменения давления от 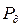 до Pф показатель адиабаты
до Pф показатель адиабаты 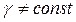 , реальную адиабату в этом случае представляют в виде:
, реальную адиабату в этом случае представляют в виде:
|
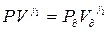 при
при 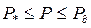 , где
, где 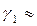 3
3
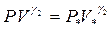 при
при 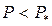 , где
, где 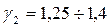
Величины 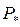 ,
, 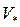 находятся по соотношениям [2]:
находятся по соотношениям [2]:
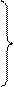
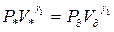
|
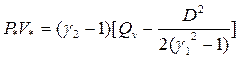
Учитывая (4.79), находим
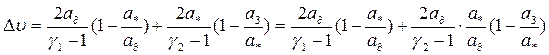
Подставляя значение 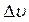 в соотношение
в соотношение 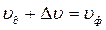 и учитывая, что
и учитывая, что 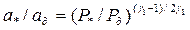 , по аналогии с (4.81) получаем
, по аналогии с (4.81) получаем
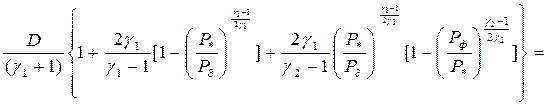
|
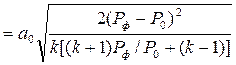
Значения начального давления во фронте воздушной ударной волны Pф и давления 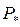 при взрывах некоторых взрывчатых веществ приведены в табл.29.
при взрывах некоторых взрывчатых веществ приведены в табл.29.
Таблица 29
Значения начального давления P ф и давления 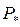
| Взрывчатое вещество (ВВ) | Плотность ВВ
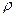 , кг/м3 , кг/м3
| Теплота взрыва. Qv, МДж/кг | Давление | |
| Pф, кПа | 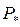 , кПа , кПа
| |||
| Тротил | 4,52 | 67·103 | 152·103 | |
| Тэн | 5,87 | 96·103 | 181·103 |
§4.9. Нормальное отражение плоской ударной волны от абсолютно жесткой стенки
Пусть на бесконечную абсолютно жесткую стенку падает по нормали к её поверхности плоская ударная волна, рис. 33“а”
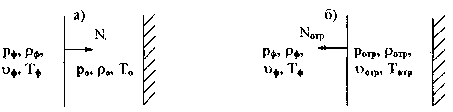
Рис.33. Отражение плоской ударной волны от жесткой стенки
Параметры невозмущенной среды на этом рисунке обозначены через p0, r0, Т0, и u0, параметры среды за фоном ударной волны через рф, rф, uф, Тф; скорость перемещения фронта N.
В момент встречи ударной волны со стенкой возникает отраженная волна, распространяющаяся в обратном направлении со скоростью Nотр, рис.33”б”. Её параметры обозначены через ротр, rотр, uотр, Тотр.
Нормальная составляющая скорости частиц на стенке по условиям задачи равна нулю.
Согласно формуле (4.50), для скорости воздуха в ударной волне имеет место соотношение
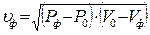 ,
,
где V0=1/r0, Vф=1/rф
Аналогично
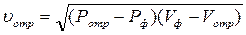 (4.85)
(4.85)
Принимая во внимание, что на стенке uотр - uф = 0, нетрудно получить
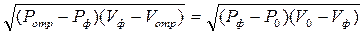
или
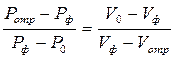 (4.86)
(4.86)
Соотношение (4,86) может быть преобразовано к виду
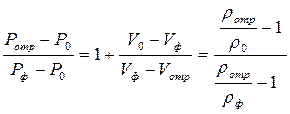 (4.87)
(4.87)
Согласно (4.54) выполняются соотношения:
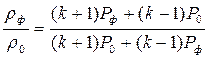 и
и 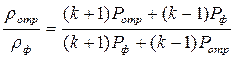
Исключая с помощью этих соотношений величины rотр и rф из (4.87), можно получить [4]
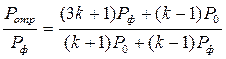 (4.88)
(4.88)
Формула ( 4.88 ) носит название формулы Измайлова (более строго Измайлова-Крюссара). Она может быть приведена к виду
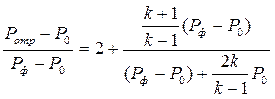 (4.89)
(4.89)
Или, что то же
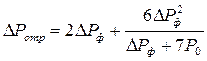 (4.90)
(4.90)
Из формул (4.89), (4.90) следует, что для ударной волны малой амплитуды (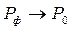 )
)
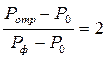
Таким образом, давление на преграде удваивается по сравнению с давлением за фронтом прямой волны, что совпадает с известным результатом отражения акустических волн.
В другом предельном случае, когда 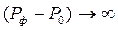 , при k =1,4
, при k =1,4
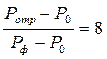
Используя соотношения (4.50), можно найти остальные гидродинамические элементы волн у стенки, а именно:
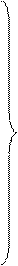
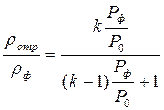
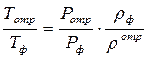 (4.91)
(4.91)

Представляет интерес сопоставления давления отражения при падении ударной волны на жесткую стенку, определяемого формулой (4.90), с давлением заторможенного потока, рассчитываемого по интегралу Бернулли (4.18)
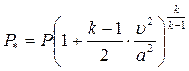
Подставив в данное выражение значения скорости газа u, скорости звука из ( 4.54), заменив давление P на Pф, можно получить
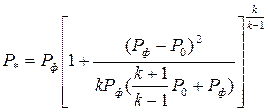 (4.92)
(4.92)
Формула (4.92) получена Ю.Б. Харитоном [4].
Если рассматривается падение ударной волны не на жёсткую стенку, а преграду конечных размеров типа промышленного или жилого здания, то после прохождения ударной волны здания, сооружения и окончания дифракционных процессов устанавливается режим обтекания.
Силовое воздействие на преграду в режиме установившегося обтекания определяется зависимостью
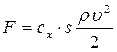 , (4.93)
, (4.93)
где, cx – коэффициент лобового сопротивления рассматриваемого объекта;
s –площадь его поперечного сечения.
Подставляя в данное соотношение значения r, u из ( 4.54 ), можно получить
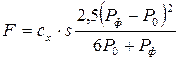 , (4.94)
, (4.94)
Значения коэффициента cx обычно находятся экспериментально при продувках в аэродинамических трубах.
На рис.34 приведено сопоставление величин давления отражения ∆Ротр=Ротр–Ро ,давления в заторможенном потоке ∆Р*=Р*–Ро и давления в установившемся режиме обтекания 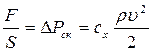 для прямоугольной пластины, расположенной по нормали к направлению потока при ∆Рф <400 кПа.
для прямоугольной пластины, расположенной по нормали к направлению потока при ∆Рф <400 кПа.
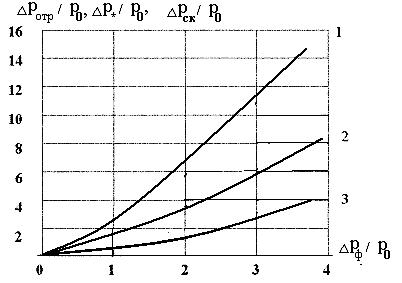
Рис.34. Давление отражения и скоростного напора в сопоставлении с давлением в заторможенном потоке
1 – давление отражения,
2 – давление в заторможенном потоке,
3 – давление скоростного напора
Из рисунка видно, что отношение ∆Р*/∆Ротр»1/2.Данный результат играет важную роль при оценке внешних сил, возникающих на преграде при воздействии воздушной ударной волны.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1627; Нарушение авторских прав?; Мы поможем в написании вашей работы!