
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Детонационная волна
|
|
|
|
Как отмечалось в §1.7, процессы взрывчатого превращения могут быть подразделены на взрывное горение и детонацию. Взрывное горение протекает со скоростями распространения пламени от нескольких десятков до нескольких сотен метров в секунду, но меньших скорости звука во взрывчатом веществе; процесс детонации распространяется со скоростью, превышающей скорость звука в данном ВВ. В передаче горения по веществу определяющую роль играют процессы теплопроводности, в передаче детонации – ударная волна. Взрывное горение при определенных условиях может скачкообразно перейти во взрыв в форме детонации.
Взрыв многих взрывчатых веществ, используемых в инженерной практике и военном деле, происходит в режиме детонации. Он относится к числу наиболее опасных, приводящих к наибольшим разрушениям.
Установлено, что если при инициировании взрыва амплитуда давления во фронте ударной волны, распространяющейся по взрывчатому веществу, больше некоторой критической величины, то волна при своем распространении способна за своим фронтом в относительно узкой зоне возбудить интенсивную химическую реакцию с выделением большого количества энергии, за счет которой поддерживается постоянство параметров волны в процессе ее дальнейшего распространения,- такая волна называется детонационной. Скорость распространения фронта подобной волны является постоянной величиной и носит название скорости детонации.
Граничную поверхность, отделяющую зону химической реакции за фронтом ударной волны от конечных продуктов детонации, называют поверхностьюЧепмена-Жуге, давление на ней - давлением детонации или давлением в точке Жуге.
При количественном описании детонационной волны обычно сопоставляют параметры состояния исходного взрывчатого вещества (P1, 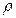 1,T1) и конечных продуктов (P2,
1,T1) и конечных продуктов (P2, 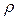 2,T2). При этом размеры (ширину) зоны химической реакции допустимо не рассматривать.
2,T2). При этом размеры (ширину) зоны химической реакции допустимо не рассматривать.
На фронте детонационной волны уравнения сохранения массы и количества движения имеют тот же вид, что и на фронте ударной волны:
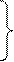
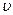 2=
2=  , (4.60)
, (4.60)
D=V1 · 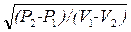
где через D обозначена скорость перемещения фронта детонационной волны, V1 =  , V2 =
, V2 = 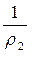 - удельные объемы.
- удельные объемы.
Уравнение сохранения энергии записываются следующим образом
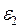 -
- 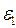 =
= 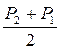 (V1-V2) + Qv, (4.61)
(V1-V2) + Qv, (4.61)
где Qv - удельная энергия взрывчатого превращения, выделяемая при химической реакции.
Зная уравнения состояния продуктов детонации и исходной среды, исключая из (4.61) величины 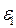 и
и 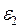 , можно получить уравнение, связывающее P2, V2 с P1, V1, Qv, - аналог адиабаты Гюгонио для продуктов детонации во фронте детонационной волны.
, можно получить уравнение, связывающее P2, V2 с P1, V1, Qv, - аналог адиабаты Гюгонио для продуктов детонации во фронте детонационной волны.
Особенности этой адиабаты рассмотрены К.П. Станюковичем [2]. Прежде всего, на ней величина Qv везде постоянна, следовательно, dQv =0. Полагая постоянными P1, V1, 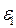 , можно записать
, можно записать
d 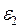 =
=  [ dP2 (V1-V2) – (P2+P1) dV2 ] = T2dS2 – P2dV2
[ dP2 (V1-V2) – (P2+P1) dV2 ] = T2dS2 – P2dV2
С учетом представления производной dP2/dV2= 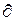 P2/
P2/ 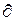 V2+
V2+
+(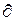 P2/
P2/ 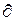 S2)(dS2/dV2), это соотношение можно представить в виде
S2)(dS2/dV2), это соотношение можно представить в виде
|
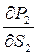 (V1-V2)]
(V1-V2)] 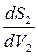 =
=  (V1-V2) + (P2-P1)
(V1-V2) + (P2-P1)
Необходимо отметить, что величины P1, V1 не лежат на рассматриваемой адиабате, поскольку при V2=V1, P2=P1, 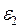
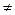
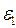 , так как при V2=V1 величина
, так как при V2=V1 величина 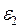 =
= 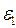 +Qv.
+Qv.
В отличие от адиабаты для ударной волны, адиабата для продуктов детонации может иметь две точки, в которых dS 2=0. В этих точках, как следует из (4.62)
|
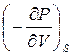 =
= 
Следует отметить, что различным участкам адиабаты (4.62) могут соответствовать различные режимы движения среды. Обозначив верхнюю точку касания буквой Д, нижнюю буквой Г и точки пересечения с адиабатой прямых линий V=V1 и P=P1 буквами В и Р, получаем пять участков: выше точки Д, между Д и В, между В и Р, между Р и Г и ниже точки Г, рис. 31.
Опираясь на соотношение (4.62), можно установить значение dS на различных участках этой адиабаты.
Остановимся на режимах движения среды, соответствующих точкам Д и Г. Данное движение описывается уравнениями (4.60), (4.61) и (4.63). Поскольку скорость звука равна 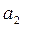 = V2 ·
= V2 ·  , можно записать
, можно записать
D -  2 = V1 ·
2 = V1 · 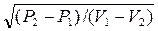 -
- 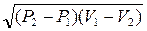 =
=
= V2 ·  = V2 ·
= V2 · 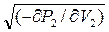 =
= 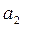
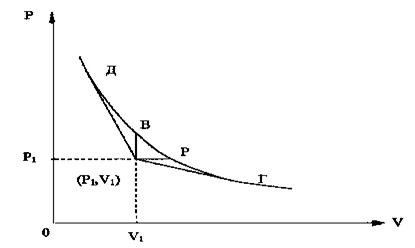
Рис. 31. Адиабата продуктов детонации
Из приведенного выше соотношения следует
|
 2+
2+ 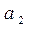
В точке Д P2>P1, V2<V1, скорость 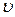 2 направлена в сторону движения фронта и, кроме того, D >
2 направлена в сторону движения фронта и, кроме того, D > 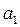 , где
, где 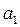 – скорость звука в исходной среде; режим движения в данном случае отвечает детонационной волне, распространяющейся с постоянной скоростью D=
– скорость звука в исходной среде; режим движения в данном случае отвечает детонационной волне, распространяющейся с постоянной скоростью D=  2+
2+ 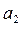 . Этот случай обычно и наблюдается при взрыве зарядов ВВ.
. Этот случай обычно и наблюдается при взрыве зарядов ВВ.
В точке Г P2<P1, V2>V1, скорость  2 направлена относительно движения фронта в противоположную сторону, поскольку P2<P1, при этом D < a 1 – режим движения отвечает горению.
2 направлена относительно движения фронта в противоположную сторону, поскольку P2<P1, при этом D < a 1 – режим движения отвечает горению.
Выше точки Д значения P2>P1, V2<V1, 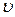 2+
2+  > D, D >
> D, D > 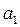 . В этом случае любое возмущение давления за фронтом детонационной волны догонит фронт волны и повлияет на его движение; такая волна называется “пересжатой”. К пересжатым нестационарным детонационным волнам относят сферические и цилиндрические сходящиеся детонационные волны, а также детонационную волну, распространяющуюся из трубы с большим сечением в трубу с меньшим сечением.
. В этом случае любое возмущение давления за фронтом детонационной волны догонит фронт волны и повлияет на его движение; такая волна называется “пересжатой”. К пересжатым нестационарным детонационным волнам относят сферические и цилиндрические сходящиеся детонационные волны, а также детонационную волну, распространяющуюся из трубы с большим сечением в трубу с меньшим сечением.
Ниже точки Д на участке ДВ имеют место соотношения P2>P1, V2<V1, 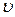 2 +
2 +  <D, D>
<D, D> 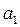 . Подобный режим называют режимом слабой детонации. Поскольку
. Подобный режим называют режимом слабой детонации. Поскольку 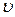 2+
2+  < D, элементарные волны давления не будут догонять фронт волны; этот режим является неустойчивым. При обычных условиях взрыва он не наблюдается.
< D, элементарные волны давления не будут догонять фронт волны; этот режим является неустойчивым. При обычных условиях взрыва он не наблюдается.
Участок адиабаты между точками В и Р не соответствует никаким случаям фронтального горения, то есть горения или взрыва с резко выраженным фронтом, поскольку на этом участке P2>P1, V2>V1 и величины скоростей D и 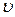 2 оказываются мнимыми.
2 оказываются мнимыми.
Участок адиабаты между точками Р и Г соответствует режиму слабой дефлаграции, то есть режиму медленного горения; в этом случае P2<P1, V2>V1, 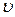 2+
2+  > D, D <
> D, D < 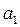 .
.
Ниже точки Г значения P2<P1, V2>V1, 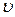 2+
2+  < D, D <
< D, D < 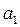 – режим горения, называемый сильной дефлаграцией или быстрым горением. При обычных условиях горения он не осуществляется (его можно осуществить, только сначала подведя тепло, а затем его отнимая).
– режим горения, называемый сильной дефлаграцией или быстрым горением. При обычных условиях горения он не осуществляется (его можно осуществить, только сначала подведя тепло, а затем его отнимая).
В обычных условиях максимальная скорость дефлаграционного горения имеет место при режиме, отвечающем точке Г.
Как отмечалось, в условиях реальных (не специальных) взрывов режиму детонации отвечает движение, соответствующее точке Д. Для количественной оценки основных параметров детонационной волны (P2,  ,
, 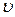 2, T2, D) можно воспользоваться следующей системой уравнений:
2, T2, D) можно воспользоваться следующей системой уравнений:
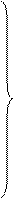 D=V1 ·
D=V1 · 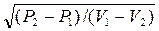
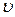 2=
2= 
|
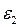 -
- 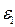 =
= 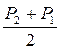 · (V1-V2)+ Q
· (V1-V2)+ Q
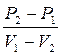 =
=  =
= 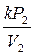
P2=f( ,T2)
,T2)
Последнее уравнение есть уравнение состояния, имеющее различный вид в зависимости от рассматриваемого взрывчатого вещества (газовые взрывчатые системы, конденсированные ВВ). Система уравнений (4.65) позволяет однозначно определить искомые величины P2,  ,
,  , T2, D.
, T2, D.
Рассмотрим вначале взрыв газовоздушной системы. Уравнение состояния записывается в виде
P= 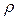 RT=
RT= 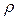 CvT(k-1)
CvT(k-1)
Так как в точке Д dS=0, имеет место PV k=const, при этом  =PV/(k-1), -dP/dV=kP/V. Тогда уравнение энергии преобразуется к виду:
=PV/(k-1), -dP/dV=kP/V. Тогда уравнение энергии преобразуется к виду:
|
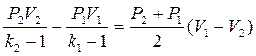 + Qv ,
+ Qv ,
где k1 (для исходной смеси) и k2 (для продуктов детонации) в общем
случае могут иметь различные значения.
При взрывах газовоздушных смесей допускается принимать k1=k2= 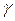 .
.
Подставляя в уравнение (4.65) величины k1=k2= 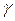 , V1=1/
, V1=1/  , V2=1/
, V2=1/ 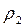 , получаем
, получаем
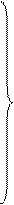

(4.67)
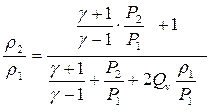
Соотношения (4.67) – аналог адиабаты Гюгонио для продуктов детонации в рассматриваемом случае взрыва.
В точках Д и Г условие (4.63) или, что то же самое, четвертое уравнение системы (4.65), определяет значение удельных объемов
|
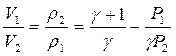
Используя данное соотношение, можно записать
|
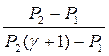
Подставляя величину V1-V2 из (4.69) в первое и второе уравнение системы (4.65), можно получить
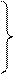
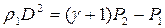
|
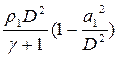
Далее определяются
|
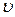 2=
2= 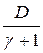
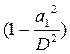
|

Сравнивая формулы (4.70)-(4.72) с формулами (4.56)-(4.58), можно отметить, что при значениях D=N и 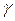 = k величины (P2-P1),
= k величины (P2-P1), 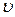 2, (V1-V2)/ V1, рассчитанные по (4.70)-(4.72), оказываются вдвое меньшими, чем аналогичные величины, определенные по (4.56)-(4.58). Данный результат объясняется тем, что отношение плотностей
2, (V1-V2)/ V1, рассчитанные по (4.70)-(4.72), оказываются вдвое меньшими, чем аналогичные величины, определенные по (4.56)-(4.58). Данный результат объясняется тем, что отношение плотностей 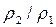 согласно (4.67) вследствие выделения тепла в зоне химической реакции меньше, чем вычисленное по (4.54).
согласно (4.67) вследствие выделения тепла в зоне химической реакции меньше, чем вычисленное по (4.54).
Учитывая соотношение (4.68) и второе уравнение системы (4.65), можно записать
 .
.
Исключая далее из уравнения сохранения энергии величину V2, можно получить
|

В этом уравнении, как и раньше, 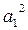 =
= 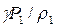 . Решение данного уравнения получено в виде [2]:
. Решение данного уравнения получено в виде [2]:
|
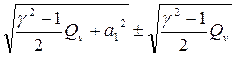 ,
,
где знак (+) соответствует режиму детонации в точке Д, знак (-) – дефлаграционному горению в точке Г.
Для типовых взрывчатых систем величина энергии, выделяемая единицей массы вещества Qv в процессе химической реакции, значительно больше, чем внутренняя энергия исходной среды, характеризуемая величиной 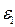 = P1V1 /(
= P1V1 /(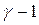 )=
)= 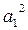 /
/  . Таким образом, можно считать, что
. Таким образом, можно считать, что  Qv >>
Qv >> 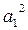 , или, тем более, Qv >>
, или, тем более, Qv >> 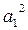 . Кроме того, при детонации газовоздушных смесей P2>>P1, D2>>
. Кроме того, при детонации газовоздушных смесей P2>>P1, D2>> 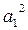 . С учетом приведенных оценок соотношения (4.70)-(4.72), (4.74) можно упростить, а именно:
. С учетом приведенных оценок соотношения (4.70)-(4.72), (4.74) можно упростить, а именно:
 D =
D = 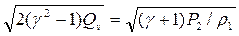
|

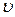 2=
2= 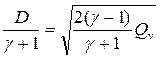
При P2>>P1 соотношение (4.68) преобразуется к виду
|
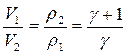
Согласно уравнению состояния
T2 = 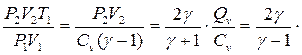 Tвзр (4.77)
Tвзр (4.77)
В соотношениях (4.75)-(4.77) величина 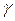 – показатель адиабаты продуктов взрыва (детонации), величина Tвзр – температура реакции взрывчатого превращения.
– показатель адиабаты продуктов взрыва (детонации), величина Tвзр – температура реакции взрывчатого превращения.
Значения Qv,  для наиболее распространенных горючих (взрывчатых) смесей приведены в табл. 32 §5.4.
для наиболее распространенных горючих (взрывчатых) смесей приведены в табл. 32 §5.4.
Величина показателя адиабаты продуктов взрыва (ПВ) 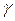 =
= 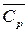 /
/ 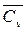 =
= 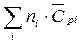 /
/ 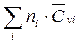 , где
, где 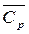 ,
, 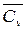 - средние теплоемкости ПВ при постоянном давлении и постоянном объеме соответственно при изменении температуры от начальной T0 до температуры взрыва Tвзр;
- средние теплоемкости ПВ при постоянном давлении и постоянном объеме соответственно при изменении температуры от начальной T0 до температуры взрыва Tвзр;
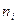 - число молей i -го ПВ;
- число молей i -го ПВ; 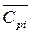 ,
, 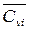 - его теплоемкости.
- его теплоемкости.
При взрыве газовоздушной смеси, содержащей горючие газы вида CaHb, реакция взрывчатого превращения отвечает соотношению (1.39)
C a Hb+(a +  )O2+3,76(a +
)O2+3,76(a + 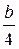 )N2= a CO2+
)N2= a CO2+ 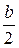 H2O+3,76(a +
H2O+3,76(a +  )N2+ Qv
)N2+ Qv
При определении показателя адиабаты ПВ воспользуемся рекомендациями § 2.6.
В приближенных расчетах величину теплоемкости 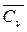 допускается представлять в виде (при 0o
допускается представлять в виде (при 0o 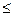 t
t 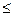 3000oC):
3000oC):
N2 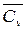 =4,96+0,0006t,
=4,96+0,0006t, 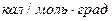
H2O (пар) 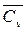 =5,96+0,00135t,
=5,96+0,00135t, 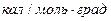
CO2 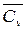 =9,0+0,00093t,
=9,0+0,00093t, 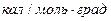
В качестве примера оценим значение показателя адиабаты ПВ при взрыве газовоздушной смеси, содержащей горючий газ метан; температуру взрыва такой смеси примем приближенно tвзр 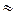 2200oC.
2200oC.
Реакция взрывчатого превращения рассматриваемой смеси имеет вид
CH4+2O2+7,52N2=CO2+2H2O+7,52N2+ Qv
Подсчитаем теплоемкости  продуктов взрыва:
продуктов взрыва:
CO2 1· (9,0 + 0,00093·2200) = 11,046
2H2O 2· (5,96 + 0,00135·2200) = 17,860
7,52N2 7,52· (4.96+0,0006·2200) = 47,225
 Всех продуктов взрыва 76,13
Всех продуктов взрыва 76,13
Величину теплоемкости Cp находим по соотношению Cp = Cv+R. В рассматриваемом случае  =
= 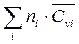 +10,52 R = 76,13+10,52·1,99 = 97,06.
+10,52 R = 76,13+10,52·1,99 = 97,06.
Показатель адиабаты продуктов взрыва:
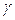 =
= 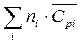 /
/ 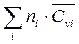 =97,06/76,13=1,27.
=97,06/76,13=1,27.
Для сравнения, значение этого показателя, полученное при более строгом определении температуры взрыва смеси tвзр, составляет 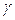 =1,26, см. табл., §5.4.
=1,26, см. табл., §5.4.
В приближенных расчетах величину 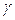 при взрыве газовоздушных смесей часто принимают равной 1,25.
при взрыве газовоздушных смесей часто принимают равной 1,25.
Взрыв конденсированных взрывчатых веществ. Как отмечалось ранее, конденсированные взрывчатые вещества – это, как правило, твердые и жидкие взрывчатые вещества.
При взрыве таких взрывчатых веществ для определения параметров детонационной волны в приближенных расчетах допускается использовать формулы (4.75)-(4.77).
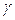 =
=  , (4.78)
, (4.78)
где 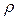 - плотность ВВ до взрыва, кг/м3.
- плотность ВВ до взрыва, кг/м3.
В приближенных расчетах величину показателя 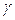 для таких взрывчатых веществ часто принимают
для таких взрывчатых веществ часто принимают 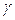
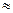 3.
3.
Пример. Определить давление во фронте детонационной волны и скорость ее распространения при взрыве тротилового заряда (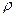 =1600 кг/м3, Qv =4,52 МДж/кг).
=1600 кг/м3, Qv =4,52 МДж/кг).
Решение. 1. По соотношению (4.78) находим величину показателя адиабаты

2. Давление во фронте детонационной волны вычисляем по второму со отношению (4.75), принимая 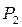 =
=  ,
,
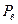 = 2(2,88-1) ·1600·4,52·106 =2,7·1010 Па
= 2(2,88-1) ·1600·4,52·106 =2,7·1010 Па
3. Скорость фронта детонационной волны определяем по первому соотношению (4.75)
D =  м/с
м/с
Пример. Определить давление во фронте детонационной волны и скорость ее распространения при взрыве газовоздушной смеси, содержащей метан (CH4). Плотность смеси до взрыва 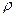 =1,23 кг/м3, теплота взрыва Qv =2,76 МДж/кг, показатель адиабаты продуктов взрыва
=1,23 кг/м3, теплота взрыва Qv =2,76 МДж/кг, показатель адиабаты продуктов взрыва  =1,26.
=1,26.
Решение. 1. Давление во фронте детонационной волны находим по второму соотношению (4.75)
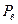 =2(1,26-1) ·1,23·2,76·106 =1,77·106 Па
=2(1,26-1) ·1,23·2,76·106 =1,77·106 Па
2. Скорость фронта волны вычисляем по первому соотношению (4.75)
D = 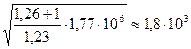 м/с
м/с
Следует отметить, что в расчетном примере по определению давления во фронте детонационной волны 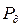 и скорости распространения фронта D при взрыве тротилового заряда значение теплоты взрыва Qv =4,52 МДж/кг принималось по таблице 5. Такое значение Qv принято согласно данным [10]. В литературе [2] она оценивается величиной Qv = 4,19 МДж/кг. При использовании теплоты взрыва Qv =4,19 МДж/кг, расчетные значения P ¶ и D будут несколько меньше.
и скорости распространения фронта D при взрыве тротилового заряда значение теплоты взрыва Qv =4,52 МДж/кг принималось по таблице 5. Такое значение Qv принято согласно данным [10]. В литературе [2] она оценивается величиной Qv = 4,19 МДж/кг. При использовании теплоты взрыва Qv =4,19 МДж/кг, расчетные значения P ¶ и D будут несколько меньше.
При необходимости уточнения  и D конденсированных ВВ можно воспользоваться экспериментальными данными и рекомендациями [2].
и D конденсированных ВВ можно воспользоваться экспериментальными данными и рекомендациями [2].
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 3000; Нарушение авторских прав?; Мы поможем в написании вашей работы!