Гидродинамические элементы во фронте ударной волны. Адиабата Гюгонио

Для простоты вывода соотношений по определению гидродинамических элементов во фронте ударной волны представим, что в трубу с площадью поперечного сечения , заполненную газом, вдвигается поршень с постоянной скоростью , рис. 29. Газ считается идеальным, а процесс адиабатическим.

Пусть начало движения отвечает моменту времени . При движении поршня при сформируется фронт ударной волны, перемещающийся со скоростью ; при этом перед фронтом ударной волны параметры среды 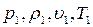, за фронтом 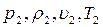. Чтобы найти соотношения между ними, необходимо воспользоваться законами сохранения массы, количества движения и энергии.

Рассмотрим закон сохранения массы. Пусть за время 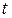поршень относительно невозмущенного газа переместиться на расстояние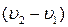 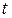, а фронт ударной волны – на расстояние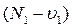 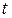. Масса сжатого газа равна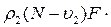 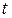. С другой стороны данная масса газа до сжатия определялась величиной 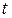. Приравнивая эти значения, получаем

(4.42)

Рассмотрим закон сохранения количества движения. Поскольку изменение количества движения данной массы газа 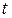равно импульсу действующей на нее силы, имеет место соотношение

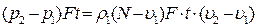
Отсюда

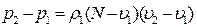(4.43)

Рассмотрим закон сохранения энергии. Для адиабатического процесса изменение полной энергии среды равно произведенной над ней работе. Обозначим внутреннюю энергию единицы массы среды через 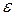, а кинетическую энергию через . Изменение энергии среды обуславливается работой внешних сил 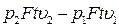, при этом

.

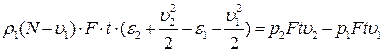Отсюда

(4.44)

Преобразуем полученное уравнение к более простому и удобному в практическом применении виду. Предварительно представим соотношение (4.42) в виде , где - удельный объем. Умножая обе части этого соотношения на 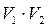, получим , отсюда 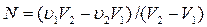. Вычитая величину 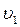из обеих частей последнего выражения, находим

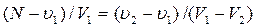(4.45)

Из соотношения (4.43) имеем 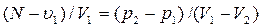. Сравнивая данное выражение с (4.45), получаем значение массовой скорости газа за фронтом ударной волны в виде:

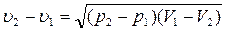(4.46)

Сравнивая далее соотношения (4.45) и (4.46), находим значение скорости перемещения фронта

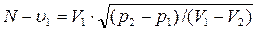(4.47)

Используя формулы (4.46), (4.47) и представив соотношение (4.44) в виде

,получаем следующую формулу закона сохранения энергии во фронте ударной волны

(4.48)

Таким образом, согласно законам сохранения массы, количества движения и энергии во фронте ударной волны должны выполняться соотношения (4.42), (4.43), (4.48), а также соотношения (4.46), (4.47).

Если газ перед фронтом ударной волны покоится, указанные соотношения упрощаются:

(4.49)

или

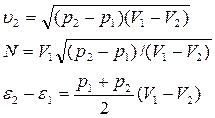(4.50)

Если газ идеальный, то , , .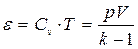

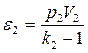Подставив значения 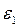и 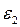в уравнение (4.48) и учитывая, что 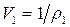, , получаем

(4.51)

Для ударных волн с избыточным давлением во фронте до нескольких сотен кПа (с некоторой погрешностью до нескольких тысяч кПа) значения . Тогда

(4.52)

Соотношения (4.51), (4.52) называются ударной адиабатой или адиабатой Гюгонио. Ударная адиабата выражает закон сохранения энергии во фронте ударной волны.

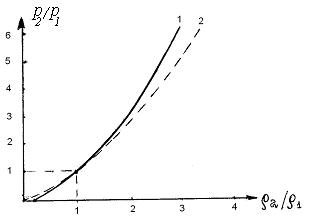
Рис.30. Сопоставление адиабаты Гюгонио и адиабаты Пуассона

1-адиабата Гюгонио, 2-адиабата Пуассона

На рис. 30 проведено составление адиабаты Гюгонио и адиабаты Пуассона, записанной в виде

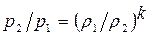
Кривые 1, 2 пересекаются в точке (1,1). При сжатии газа до одного и того же значения 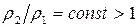согласно адиабаты Гюгонио требуется большее давление, чем по адиабате Пуассона. При 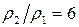(и ) отношение давлений .

Таким образом, во фронте ударной волны при больших давлениях сжатия плотность возрастает сравнительно медленно, что связано с быстрым ростом температуры при ударном сжатии газа.

Величина температуры во фронте вычисляется из уравнения состояния идеального газа. Так как 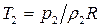, , то

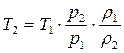(4.53)

Уравнения (4.46), (4.47), (4.52), (4.53) представляют собой систему четырех уравнений при пяти неизвестных. Задаваясь значением какого-либо одного из параметров ударной волны, можно определить значения остальных.

Например, значения скорости перемещения газа, плотности фронта и скорости температуры в зависимости от отношения имеют вид:

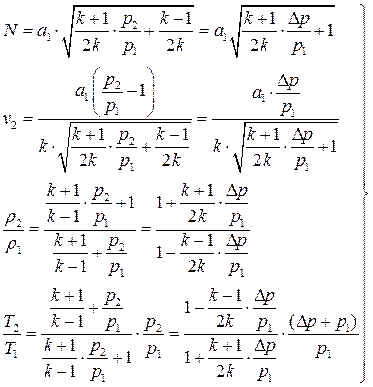, (4.54)

где величина 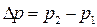, - скорость звука в невозмущенной среде.

Представляется полезным выразить основные параметры ударной 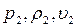как функции скорости звука невозмущенного газа. Положив , обозначив 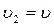и используя уравнение состояния , можно представить соотношение (4.43) в виде

(4.55)

Подставив в данное выражение значение 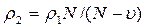из (4.42) и 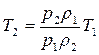, после преобразований можно получить

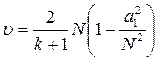(4.56)

Заменяя в выражении (4.55) скорость 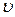ее значением из (4.56), находим

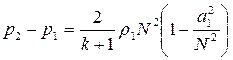(4.57)

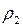Аналогично, заменяя на и на , можно получить

(4.58)

Из соотношений (4.56)-(4.58) следует, что для ударных волн, когда 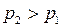, всегда 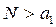, , причем , то есть среда (газ) перемещается в направлении распространения фронта, но с меньшей, чем у фронта скоростью. Наоборот, при и 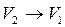, величины , , 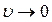и ударная волна вырождается в звуковую.

Представляет интерес также оценка энтропии во фронте ударной волны. Согласно соотношению (1.13) энтропия идеального газа может быть представлена в виде .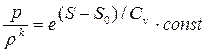

Обозначим правую часть этого соотношения через . В невозмущенном газе 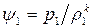, после сжатия его ударной волной . Подставляя в последнее соотношение значение 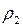из (4.54), находим

(4.59)

Таким образом, энтропия среды при 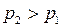, то есть при прохождении через нее ударной волны, возрастает.

Наоборот, при значение .

Дата добавления: 2014-12-27