
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Косое падение ударной волны на твердую поверхность
|
|
|
|
Косое падение (падение под углом) ударной волны на твердую поверхность – сложный газодинамический процесс. Его рассмотрение целесообразно начать с более простого случая падения волны бесконечно малой амплитуды. В такой постановке задача отражения волн называется задачей акустического приближения.
Пусть плоская акустическая волна падает на абсолютно жесткую поверхность в точке "О", причем фронт волны составляет угол a с границей. Параметры среды за фронтом волны обозначим через 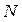 ,V, p,
,V, p, 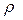 . В момент встречи ударной волны со стеной возникает отраженная волна с параметрами
. В момент встречи ударной волны со стеной возникает отраженная волна с параметрами 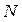 ’,V ‘, p’,
’,V ‘, p’, 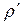 , рис35.
, рис35.

N’ V
V ‘cosa’ V cosa
V ‘ a’ a N
A B
O
Рис. 35. Схема отражения акустических волн
Нормальная составляющая скорости частиц воздуха на стенке по условиям задачи (стенка абсолютно жесткая) равна нулю. Иначе говоря, на стенке должно выполняться соотношение
V 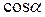 -V ‘
-V ‘ 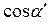
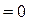
 (4.95)
(4.95)
В случае малых возмущений как прямая, так и отраженные волны распространяются со скоростью, равной скорости звука, то есть 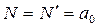 , при этом
, при этом 
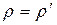 .
.
Фронты падающей и отраженной волн имеют общую точку пересечения "О" на границе АВ. Скорость перемещения этой точки вдоль границы определяется по соотношению
 (4.96)
(4.96)
Из данного равенства следует известный закон акустического отражения, согласно которому 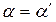 . Но тогда и V= V ‘. А так как согласно (4.49) давление на фронте волны определяется соотношением
. Но тогда и V= V ‘. А так как согласно (4.49) давление на фронте волны определяется соотношением 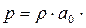 V,
V, 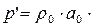 V ‘, то
V ‘, то 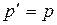 .
.
В точке "О" имеет место сложение волн. При этом давление на стенке независимо от направления распространения падающей волны (кроме случая a=p/2) всегда будет равно 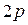 . При a=p/2 отражение волны не происходит; волна скользит вдоль стенки и давление на стенке равно
. При a=p/2 отражение волны не происходит; волна скользит вдоль стенки и давление на стенке равно 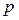 .
.
Сформулированное следствие о величине давления на стенке при падении акустической волны известно под названием акустического парадокса.
Самостоятельный интерес представляет случай, когда волна отражается не от абсолютно жесткой стенки, а от границы раздела двух сжимаемых
сред. Здесь, кроме прямой и отраженной волн, образуется преломленная волна, распространяющаяся во второй среде, рис. 36.
 N’ V
N’ V
V ‘ N
a’ a
A V “ a” O B
Рис. 36. Схема падения акустической волны на границу раздела двух сжимаемых сред
Так как точка "О" является общей для всех трех волн, ее скорость движения вдоль границы АВ определяется по соотношению
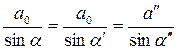 (4.97)
(4.97)
Соотношение (4.97) известно как закон Снеллиуса. Как и в первом случае, здесь справедлив закон отражения 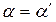 , а также имеют место соотношения
, а также имеют место соотношения 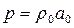 V,
V, 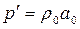 V ‘,
V ‘, 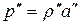 V “.
V “.
Следует отметить, что произведение 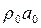 , являющееся коэффициентом пропорциональности между давлением и скоростью частиц, называется акустическим сопротивлением среды.
, являющееся коэффициентом пропорциональности между давлением и скоростью частиц, называется акустическим сопротивлением среды.
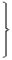 Непрерывность давления и скорости движения частиц на границе раздела сред требует выполнения равенств:
Непрерывность давления и скорости движения частиц на границе раздела сред требует выполнения равенств:
|
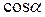 - V ‘
- V ‘ 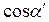 =V “
=V “ 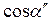
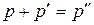
Отсюда нетрудно получить
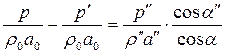
или
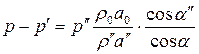 (4.99)
(4.99)
Принимая во внимание, что 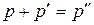 , находим
, находим
|

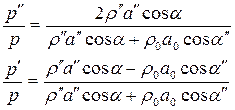
Используя соотношение 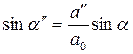 , следующее из закона Снеллиуса, формулы (4.100) можно привести к виду
, следующее из закона Снеллиуса, формулы (4.100) можно привести к виду
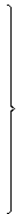
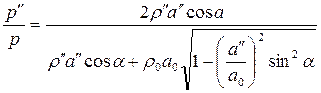
|
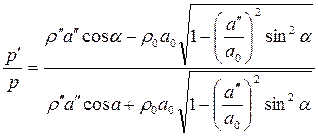
Анализ последних соотношений показывает, что если а” < а0 , то при любых углах падения прямой волны имеют место отраженная и преломленная волны.
При а”>а0 правые части соотношений (4.101), называемые часто коэффициентами отражения и преломления, действительны только в определенном диапазоне углов падения 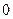
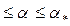
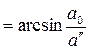 .
.
Угол  =
= 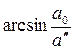 называется углом полного внутреннего отражения.
называется углом полного внутреннего отражения.
При 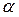 >
>  коэффициент отражения
коэффициент отражения 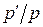 становится комплексным с модулем равным единице. Это означает, что поток энергии через границу раздела двух сред отсутствует. Преломленная волна не формируется, волновые возмущения, возникшие у поверхности раздела, быстро затухают по амплитуде по мере увеличения глубины проникновения вторую среду.
становится комплексным с модулем равным единице. Это означает, что поток энергии через границу раздела двух сред отсутствует. Преломленная волна не формируется, волновые возмущения, возникшие у поверхности раздела, быстро затухают по амплитуде по мере увеличения глубины проникновения вторую среду.
При прямом падении волны по нормали к поверхности 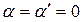 формулы (4.101), (4.102) принимают особенно простой вид
формулы (4.101), (4.102) принимают особенно простой вид
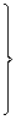
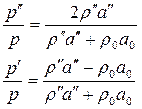 (4.102)
(4.102)
Основные следствия решения (4.101), (4.102).
1. При отражении волны, распространяющейся в воздухе, от среды, акустическое сопротивление которой больше акустического сопротивления воздуха, отраженная волна является волной сжатия p’/p >0, при этом давление во фронте преломленной волны будет больше, чем давление в прямой волне.
2. При отражении той же волны от среды, акустическое сопротивление которой меньше акустического сопротивления воздуха, отраженная волна будет волной разрежения p’/p <0, при этом давление во фронте преломленной волны будет меньше, чем давление во фронте прямой волны.
3. Отдельно можно отметить, что отраженная волна не возникает не только тогда, когда тождественно равны между собой акустические свойства сред. Приравняв нулю числитель второго соотношения (4.101), можно получить 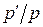
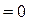 при
при 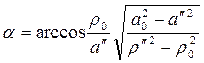 .
.
Рассмотрим далее отражение от жесткой стенки ударной волны конечной амплитуды.
Пусть угол падения прямой волны равен 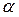 (как и в случае, представленном на рис. 35). Равенство нулю нормальной составляющей скорости частиц на стенки приводит к соотношениям:
(как и в случае, представленном на рис. 35). Равенство нулю нормальной составляющей скорости частиц на стенки приводит к соотношениям:
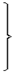 Vф
Vф 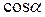 - Vотр
- Vотр 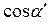 =0
=0
|
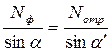
Отличие от ранее рассмотренного случая состоит в том, что здесь 
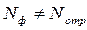 , и скорости перемещения ударных волн отличаются от скорости звука в невозмущенной среде а0 .
, и скорости перемещения ударных волн отличаются от скорости звука в невозмущенной среде а0 .
Два уравнения (4.103) включают 6 переменных: 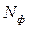 , Vф,
, Vф, 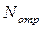 , Vотр,
, Vотр, 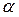 ,
, 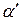 . Для их определения, необходимо, кроме уравнений (4.103), дополнительно привлечение соотношений (4.54), (4.91), однозначно связывающих величины
. Для их определения, необходимо, кроме уравнений (4.103), дополнительно привлечение соотношений (4.54), (4.91), однозначно связывающих величины 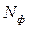 , Vф,
, Vф, 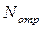 , Vотр с давлением падающей волны
, Vотр с давлением падающей волны 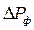 .
.
Согласно [2,4], численное решение системы уравнений (4.103), (4.54), (4.91), при заданных интенсивности прямой волны и угле падения 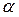 дает два значения угла
дает два значения угла 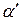 и, следовательно, два значения соответствующих ему величин Vотр и
и, следовательно, два значения соответствующих ему величин Vотр и  . Последние параметры определяют два значения
. Последние параметры определяют два значения  . Только в предельном случае бесконечно слабых волн имеет место равенство углов падения и отражения. Этот случай был рассмотрен ранее.
. Только в предельном случае бесконечно слабых волн имеет место равенство углов падения и отражения. Этот случай был рассмотрен ранее.
Экспериментально установлено, что при косом падении ударной волны конечной амплитуды на твердую поверхность обычно реализуется отражение с меньшим углом 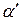 из двух возможных его значений. Кроме того, выяснено, что при увеличении угла падения
из двух возможных его значений. Кроме того, выяснено, что при увеличении угла падения 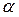 два значения
два значения 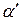 сближаются. При некотором угле
сближаются. При некотором угле 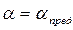 эти значения
эти значения 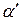 сливаются.
сливаются.
Линейное (регулярное) отражение, характерной особенностью которого является существование одной общей точки для прямой и отраженной волн, лежащей на граничной поверхности, возможно лишь при 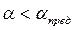 .
.
При 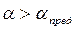 линейное отражение становится невозможным. Отраженная волна, распространяясь по возмущенной среде, догоняет прямую и, сливаясь с ней, образует третью волну, называемую волной Маха или головной ударной волной. Возникает трехволновая конфигурация, характерной особенностью является существование общей точки пересечения волн над отражающей поверхностью - так называемой «тройной» точки, рис.37. Такое отражение называется нелинейным (или нерегулярным).
линейное отражение становится невозможным. Отраженная волна, распространяясь по возмущенной среде, догоняет прямую и, сливаясь с ней, образует третью волну, называемую волной Маха или головной ударной волной. Возникает трехволновая конфигурация, характерной особенностью является существование общей точки пересечения волн над отражающей поверхностью - так называемой «тройной» точки, рис.37. Такое отражение называется нелинейным (или нерегулярным).
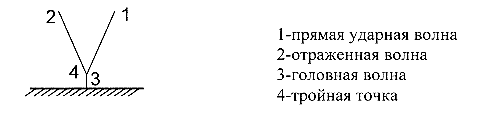
Рис. 37. Волновая система при нерегулярном отражении
ударной волны от жесткой стенки
На рис 38. представлены значения 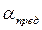 для идеального газа в зависимости от отношения давления в невозмущенной среде
для идеального газа в зависимости от отношения давления в невозмущенной среде 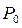 и давления в прямой волне
и давления в прямой волне 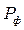 . Кривая
. Кривая 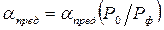 делит область значений угла
делит область значений угла 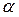 на две части: область, где возможно линейное отражение и область, где происходит нелинейное отражение.
на две части: область, где возможно линейное отражение и область, где происходит нелинейное отражение.
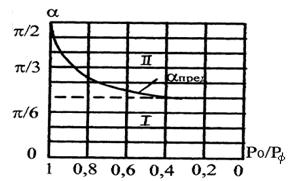
Рис. 38. Области регулярного и нерегулярного отражения
- область регулярного отражения,
- область нерегулярного отражения
Из рис. 38 видно, что, начиная с 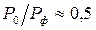 и до
и до 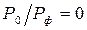 , предельный угол
, предельный угол 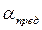 составляет около 400.
составляет около 400.
Вследствие сложности газодинамических процессов, имеющих место при косом падении ударной волны на преграду, большое значение при количественном определении параметров образующейся волновой системы имеют опытные данные.
В нашей стране наиболее законченные экспериментальные исследования рассматриваемой задачи выполнены М.А.Садовским, К.Е.Губкиным, А.И.Коротковым.
Установлено, что в области регулярного отражения для давлений во фронте 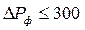 кПа величина давления в отраженной волне практически не зависит от угла падения и может быть определена по формуле Измайлова (4.90)
кПа величина давления в отраженной волне практически не зависит от угла падения и может быть определена по формуле Измайлова (4.90)
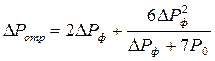 ,
,
где 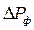 - давление в прямой волне.
- давление в прямой волне.
В области нерегулярного отражения давление во фронте головной волны может быть определено с помощью графиков рис.39 [16].
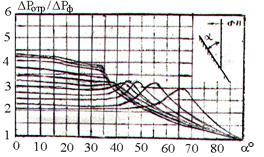
Рис.39. Давление отражения на плоской преграде при косом падении фронта ударной волны.
При пользовании графиками рис.39 вначале по формуле (4.90) для заданного давления 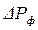 вычисляют давление
вычисляют давление 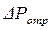 и далее находят отношение
и далее находят отношение 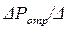 Pф. Определяют соответствующую кривую
Pф. Определяют соответствующую кривую 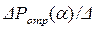 Pф при
Pф при 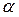 =0, с которой снимают значение
=0, с которой снимают значение 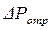 при заданном значении
при заданном значении 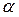 .
.
Продолжительность фазы сжатия и импульс давления в фазе сжатия отраженной и головной волн находятся согласно рекомендаций, приведенных в §5.1.
Исследование случая косого падения ударной волны конечной амплитуды на границу раздела двух сжимаемых сред выходит за рамки настоящего пособия. При необходимости с результатами решения этой задачи можно ознакомиться, например, по литературе [4].
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1309; Нарушение авторских прав?; Мы поможем в написании вашей работы!