Геометрическая интерпретация комплексного числа

Комплексные числа, как и действительные, допускают простую интерпретацию, если вместо координатной прямой использовать координатную

плоскость.

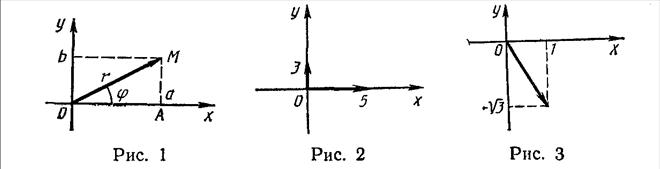
Комплексное число 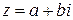изображается на координатной плоскости точкой M 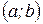или вектором 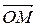, начало которого совпадает с началом координат, а конец – с точкой M (рисунок 1).

Сама координатная плоскость называется при этом комплексной плоскостью, ось абсцисс – действительной осью, а ось ординат – мнимой осью.

Модулем комплексного числа называется абсолютная величина вектора, соответствующего этому числу. Для модуля числа 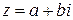используются обозначения 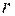, 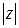или .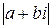

На основании теоремы Пифагора (рисунок 1) получается формула:

.

Рисунок 3

Рисунок 2

Рисунок 1

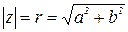Например, комплексное число 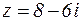имеет модуль равный 10, так как .

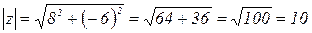Аргументом комплексного числа 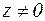называется величина угла 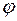между положительным направлением действительной оси и вектором, соответствующим этому числу (рисунок 1).

Для аргумента числа 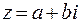используются обозначения 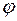, 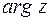или .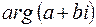

Аргумент комплексного числа 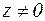в отличие от модуля определяется неоднозначно.

Так, аргументами числа 5 являются следующие углы:

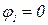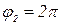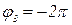, , и вообще каждый из углов 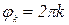, 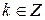; аргументом числа 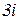– следующие углы:

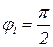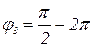, , (рисунок 2) и вообще каждый из углов , .

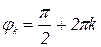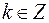Любые два аргумента комплексного числа отличаются друг от друга на слагаемое, кратное .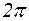

Аргумент комплексного числа 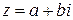можно находить так:

а) найти острый угол ;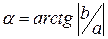

б) найти аргумент комплексного числа в зависимости от того, в какой координатной четверти лежит вектор, соответствующий этому числу: в I четверти 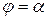; во II четверти 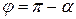; в III четверти 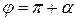; в IV четверти .

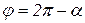Пример 4. Найти аргумент комплексного числа .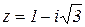

Р е ш е н и е. Находим угол 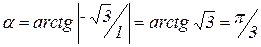. Вектор, соответствующий данному комплексному числу, лежит в IV координатной четверти (рисунок 3), поэтому аргументами числа являются каждый из углов , .

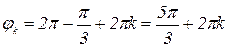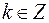Аргументы действительных и чисто мнимых чисел можно находить

непосредственно, исходя из их геометрической интерпретации, а, не используя приведённое выше правило (тем более, для чисто мнимых чисел это правило вообще нельзя применять).

Дата добавления: 2014-12-27