Непосредственное интегрирование

Основные формулы интегрирования (табличные интегралы)

Из каждой формулы дифференцирования вытекает соответствующая ей формула интегрирования. Например, из того, что 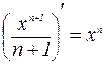, следует равенство: .

Ниже приведена таблица основных интегралов:

1 ;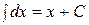

2 ;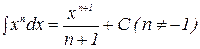

3 ;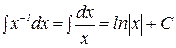

4 ;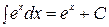

5 ;

6 ;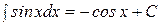

7 ;

8 ;

9 ;

10 ;

11 .

Справедливость этих формул можно проверить дифференцированием.

Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.

Пример 1. Найти интеграл: .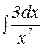

Р е ш е н и е. Воспользуемся определением степени с отрицательным показателем () и найдем неопределенный интеграл от степени:

.

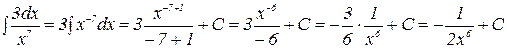Пример 2. Найти интеграл: .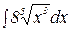

Р е ш е н и е. Воспользуемся определением степени с дробным показателем () и найдем неопределенный интеграл от степени:

.

Пример З. Найти интеграл: .

Р е ш е н и е. Воспользуемся определением степени с дробным и отрицательным показателем и правилом умножения степеней с одинаковыми основаниями () и найдем неопределенный интеграл от степени:

Пример 4. Найти интеграл: .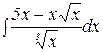

Р е ш е н и е. Воспользуемся определением степени с дробным показателем (), правилами действий над степенями с одинаковыми основаниями (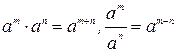), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно. Имеем

Заметим, что произвольные постоянные, входящие по определению в каждый из слагаемых неопределенных интегралов, объединяются в одну произвольную постоянную.

Пример 5. Найти интеграл: .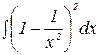

Р е ш е н и е. Раскроем скобки по формуле и неопределенный интеграл от полученной алгебраической суммы функций заменим такой же алгебраической суммой неопределенных интегралов от каждой функции:

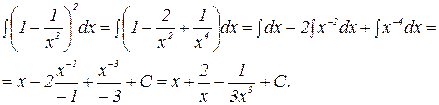
Пример 6. Найти интеграл: .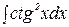

Р е ш е н и е. Для нахождения интеграла воспользуемся формулой и свойствами неопределенного интеграла:

.

Дата добавления: 2014-12-27