Свойства неопределенного интеграла

Интеграл и его приложения

3.1 Методические указания по теме «Интеграл и его приложения»

3.1.1 Неопределённый интеграл

Понятие неопределённого интеграла

Напомним, что дифференцирование – это действие, с помощью которого по данной функции находится её производная или дифференциал. Например, если 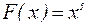, то , .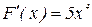

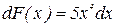Как мы знаем, нахождение производной имеет большое практическое значение. Так, по данному закону движения тела 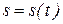мы путем дифференцирования находили скорость 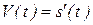, а затем и ускорение по данному уравнению кривой 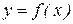определяли угловой коэффициент касательной, проведенной к этой кривой: .

На деле, однако, часто приходится решать обратную задачу: по известной скорости движения тела устанавливать закон его движения, по данному угловому коэффициенту касательной к кривой находить уравнение этой кривой и т. п., иначе говоря, по данной производной отыскивать функцию, от которой найдена эта производная, т.е. выполнять действие, обратное дифференцированию. Это действие называется интегрированием. С помощью интегрирования по данной производной или дифференциалу функции находится сама функция. Например, если , то , так как .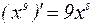

Дифференцируемая функция , 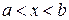называется первообразной для функции 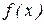на интервале 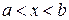, если 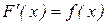для каждого .

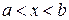Так, для функции 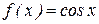первообразной служит функция , поскольку 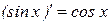для .

Для заданной функции ее первообразная определяется неоднозначно. Справедлива теорема: если – первообразная для 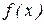на некотором промежутке, то и функция , где 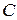– любая постоянная, также является первообразной для функции 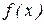на этом промежутке. Обратно: каждая функция, являющаяся первообразной для 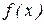в данном промежутке, может быть записана в виде .

Значит, достаточно найти для данной функции 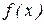только одну первообразную функцию , чтобы знать все первообразные, так как они отличаются друг от друга только на постоянную величину.

Совокупность всех первообразных функции 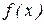на интервале 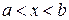называют неопределенным интегралом от функции 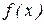на этом интервале и пишут . Здесь 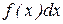– подынтегральное выражение; 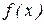– подынтегральная функция; 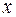– переменная интегрирования; 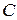– произвольная постоянная.

Например, , так как .

Если функция 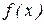имеет на некотором промежутке хотя бы одну первообразную, то ее называют интегрируемой на этом промежутке. Можно доказать, что любая функция, непрерывная на отрезке , интегрируема на этом отрезке.

1 Производная неопределенного интеграла равна подынтегральной функции; дифференциал неопределенного интеграла равен подынтегральному выражению:

, .

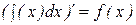2 Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной, т. е.

.

3 Постоянный множитель можно выносить за знак неопределенного интеграла:

, где .

4 Неопределенный интеграл от алгебраической суммы функций равен такой же алгебраической сумме неопределенных интегралов от каждой функции: .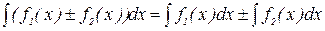

Дата добавления: 2014-12-27