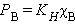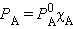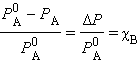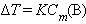Законы Рауля

Закон Генри.

Если растворенное вещество характеризуется большой упругостью пара по сравнению с упругостью пара растворителя (P_B >> P_A) и при этом оба компонента раствора химически инертны, то растворение такого газообразного вещества в жидкости подчиняется закону Генри: при постоянной температуре давление летучего (газообразного) компонента P _B прямо пропорционально его мольной доле χ_B:

(6.1)

K_H – константа Генри.

В табл. 6.1 приведены константы Генри некоторых газов для воды.

Газ	H2	He	Ar	N2	O2	CO2
KH						29,3

Таблица 6.1. Константы Генри для воды при 298 K.

Из уравнения (6.1) следует, что KH определяется выбором единиц давления и концентрации.

Если упругость пара растворенного вещества очень мала P_B << P_A, то его парциальным давлением можно пренебречь (нелетучий компонент), и тогда упругость пара над раствором будет зависеть только от парциального давления растворителя:

Это первый закон Рауля – парциальное давление над раствором прямо пропорционально мольной доле растворенного вещества. После подстановки χ_A = 1 – χ_B и несложных преобразований

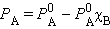
получаем

Относительное понижение упругости пара над раствором равно мольной доле растворенного вещества. Это закон Рауля для нелетучего растворенного компонента. Из этого закона можно вывести два следствия, которые в объединенном виде формируются как второй закон Рауля.

Рисунок 6.2. Зависимость повышения температуры кипения ΔT_кип и понижения температуры замерзания ΔT_зам раствора от концентрации растворенного вещества.

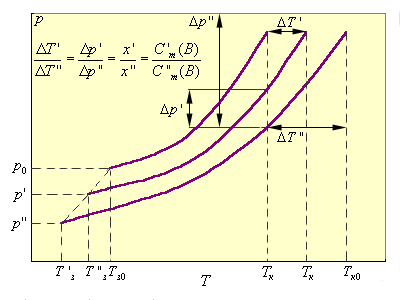
На рис. 6.2 приведены зависимости P(T) чистого растворителя и двух его растворов P'(T) и P''(T).

Выразим мольную долю 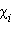через моляльную концентрацию 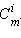Для двухкомпонентного раствора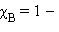 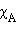. При 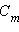<< 1 получим

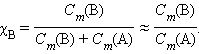
Из подобия треугольников следует

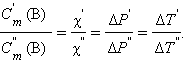
По определению, при 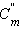(B) = 1 моль∙ 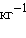повышение температуры 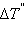равно 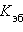– эбулиоскопической константе для данного растворителя. Тогда повышение температуры кипения для данного раствора будет пропорционально его моляльной концентрации:

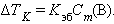
Проведя аналогичное исследование, касающееся понижения температуры замерзания раствора, получим

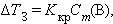
где K_кр – криоскопическая константа.

Второй закон Рауля – понижение температуры кипения и повышение температуры замерзания раствора прямо пропорционально моляльной концентрации раствора:

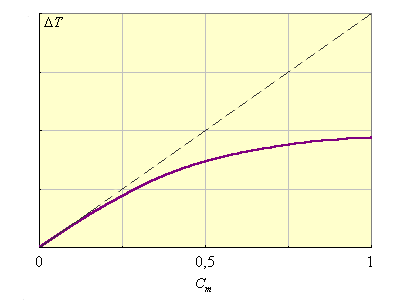
K_эб и K_кр являются экстраполяционными величинами от малых концентраций растворенного вещества, где выполняется этот закон, на C_m(B) = 1, где этот закон уже не действует (рис. 6.3). В табл. 6.2 приведены K_кр и K_эф для воды и бензола.

Рисунок 6.3. Иллюстрация справедливости второго закона Рауля для разбавленных растворов и экстраполяционной природы K_кр и K_эб.

	Kкр	Kэб
вода	1,86	0,52
бензол	5,07	2,60

Таблица 6.2. Криоскопические и эбулиоскопические константы для воды и бензола (град∙моль^–1∙кг).

Второй закон Рауля дает легко осуществимую экспериментально возможность определения молекулярных масс некоторых молекулярных соединений, неспособных к диссоциации в данном растворителе. Действительно, моляльная концентрация растворенного вещества может быть представлена в виде соотношения C_m = g_B ∙ 1000 / μ_B ∙g_A, где g_A – вес растворителя, g_B – вес растворенного вещества, μ_B – его молярная масса. Тогда из ΔT = K_кр · m получим молярную массу растворенного вещества:

Дата добавления: 2014-12-27