Дисконтированный срок окупаемости

DPP (Discounted Payback Period) исчисляется также, как и простой срок окупаемости. Но все доходы при этом дисконтируются, принимаются по своей сегодняшней приведенной ценности.

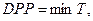
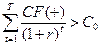(5.17)

DPP всегда больше простого PP. Величина разницы зависит от принятого уровня процентной ставки. На практике часто анализируются оба показателя (и дисконтированный и не дисконтированный срок).

Задача 138

По представленным в таблице данным о денежном потоке, генерируемом инвестицией в размере 150 000 рассчитайте простой и дисконтированный сроки ее окупаемости. Процентная ставка для расчетов – 10% за период. Сравните результаты. О чем говорит различие полученных показателей?

Периоды
Денежный поток

Простой срок окупаемости составит 4 года (30000+35000+40000+45000 = 150000)

Для оценки дисконтированного срока рассчитываем коэффициенты дисконтирования по ставке 10% и величину покрытия нарастающим итогом:

t
CF
KD	0,909	0,826	0,751	0,683	0,621	0,564	0,513
CF'
SCF'

Дисконтированный срок окупаемости такой инвестиции составит 7 лет, а не 4. Различие свидетельствует об учете фактора разновременности при заданной величине процентной ставки. Если ставка будет меньше, сократится и различие. Если ставка вырастет, вместе с ней увеличится и DPP.

Рассмотренные критерии окупаемости инвестиций рассчитываются очень легко, но часто не позволяют разрешить задачи, возникающие не в теории, а в реальной жизни. Так, часто инвестор хочет знать срок окупаемости точнее целого числа лет. Вывод пусть больших, но конечных сроков окупаемости при явной неэффективности проекта ставит методику под сомнение, т.к. по логике окупаются далеко не все инвестиции. Даже расчет дисконтированных сроков не позволяет ответить на вопрос – при каком уровне процентных ставок срок будет все-таки приемлемым, либо каким должен быть сам доход, чтобы инвестиция окупилась в обозначенные сроки. Осуществление реальных инвестиций на производстве часто предполагает их поэтапное осуществление. При этом, пошаговый расчет кумулятивного дохода может и не достичь очередной отрицательной составляющей потока независимо от того, дисконтированный поток или нет.

Желание повысить точность и учесть разновременность порождает большое количество различных формул и математических подходов к исчислению сроков окупаемости. Отметим здесь, что при дисконтировании показатели времени стоят в степени. Извлечь величину из степени можно только путем логарифмирования. Следовательно, и формула дисконтированного срока окупаемости должна содержать логарифм. Строго говоря, формализована может быть только одна частная ситуация аннуитета.

Аннуитетный поток заслуженно считается особенным, наиболее предпочтительным из всех, т.к. обладает важным свойством сворачиваться по формулам сумм прогрессий.

5.4.3. Срок окупаемости аннуитетного денежного потока*

Представим, что разовое капиталовложение величиной К генерирует впоследствии равномерный поток доходов на уровне а. Уровень процентных ставок известен. Требуется определить, когда инвестиция окупится, и окупится ли вообще при данном уровне доходов. Поставленная задача иллюстрируется схемой на рис. 21.

Рис. 21 К расчету срока окупаемости для аннуитетного денежного потока

Такая постановка задачи весьма распространена при реализации реальных инвестиций в производство. Размер взноса аннуитета – разница между увеличением доходов предприятия в каждом периоде времени (ради чего мероприятие и проводилось) и приростом его текущих затрат, если таковое присутствует. Прирост затрат может вызвать повышение размера амортизационных отчислений на новое оборудование, необходимость его технического обслуживания в соответствии с действующими требованиями, потребность в найме либо обучении персонала и т.д.

По определению, за срок окупаемости капитальное вложение К должно быть погашено доходами от него (a) с учетом приведения (дисконтирования). Принимаемую для расчетов процентную ставку обозначим r. Тогда:

(5.18)

Правая часть выражения – геометрическая прогрессия, такая же, как мы уже рассматривали в разделе 3.3 при расчете настоящей стоимости аннуитетов постнумерандо.

; ; ; .

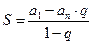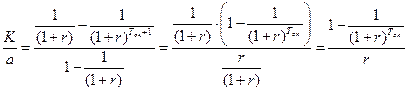
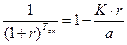
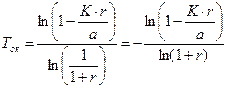(5.19)

Знак «минус» в начале формулы не случаен. Выражение – число, заведомо меньше 1. Поэтому числитель всегда будет отрицательным.

Важное значение имеет и еще один момент. Если (доли, возмещаемой ежегодно), будет отрицательно. Логарифм отрицательного числа не существует. Следовательно, не будет существовать и срок окупаемости такого вложения. В этом заключается очень существенное преимущество дисконтированных оценок перед не дисконтированными. Сколь бы значительным не было капитальное вложение, и сколь бы ничтожной не была от него отдача, не дисконтированный Т_ок будет иметь конечное значение. Дисконтированные сроки существуют не всегда, что закономерно, поскольку по логике окупаются далеко не все инвестиции.

Чтобы проиллюстрировать разницу между простым и дисконтированным сроками, приведем пример расчета по данной формуле.

Задача 139*

Пусть капитальное вложение (К) составляет 400 усл. ед. Ежегодная ожидаемая дополнительная прибыль предприятия (а) оценивается в 40 усл. ед. Процентная ставка r=5%. Рассчитать простой и дисконтированный срок окупаемости такой инвестиции. Определить, какой должна быть ежегодная дополнительная прибыль, чтобы дисконтированный срок окупаемости был равен 10 годам.

Простой (не дисконтированный) срок окупаемости составит 10 лет.

Дисконтированный срок

года

При ставке r =7% срок окупаемости составит 17,8 лет, при ставке r =9% – 26,7 лет. Если цена денег превышает 10% (а/K =40/400), данное мероприятие не окупается.

Решаем обратную задачу.

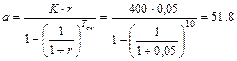усл. ед.

Задачи, разрешимые для аннуитетных денежных потоков, невозможно столь же просто разрешить, если поток не обладает свойством равномерности. Но, воспользовавшись понятием финансовой эквивалентности, можно приводить неравномерные потоки к эквивалентным аннуитетам.

5.4.4. Возможные подходы к оценке неординарных денежных потоков*

Денежные потоки считаются неординарными, если выполняется одно из следующих условий:

1. Притоки и оттоки капитала чередуются более одного раза (инвестиции осуществляются этапами);

2. Началу инвестиционного проекта соответствует приток денежных средств, окончанию – отток, либо присутствует один из этих фактов. Такая ситуация на практике встречается довольно часто. Проекты могут стартовать с получения кредитов, предоплат и т.п., а заканчиваться выплатой различных обязательств, выкупом имущества, приобретенного по лизинговым схемам, затратами на возмещение ущерба, нанесенного окружающей среде и т.д.

Такая конфигурация cash flow может свидетельствовать о том, что у проекта будет несколько значений IRR, а срок его окупаемости определится также либо умозрительно, либо в корне не верно. Приведем конкретные примеры.

Табл. 5.5

Примеры неординарных денежных потоков

Потоки	Периоды
A		-1000	-1000		-3000			-6000			-7000
B		-2000		-5000			-6000				-7000

Первый поток в силу значимости первой положительной суммы не имеет IRR вообще. При его анализе можно выявить, что NPV достигает минимума в 4516 ед. при значении r =109% и далее бесконечно стремится к 5000. Второй поток имеет два значения IRR: 86,2% и 161,6%. Оба потока «окупаются» еще до момента последней выплаты (моменты т.н. «окупаемости» у них возникают несколько раз). При этом, оба потока показывают положительные значения NPV при приемлемых уровнях процентных ставок.

Суть приведения для целей более глубокой оценки сводится к следующему: разделить значение NPV на две составляющие: часть приведенных отрицательных компонент (затрат инвестора) и часть приведенных положительных потоков (его доходов):

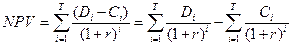(5.20)

Далее величину приведенных затрат рассматриваем, как единовременную начальную инвестицию, а сумму приведенных доходов – как настоящую стоимость аннуитета постнумерандо продолжительностью Т при ставке r.

(5.21)

(5.22)

Величина единичного дохода тогда может быть определена по формуле:

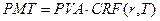, где 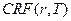- стандартная единичная функция для заданных условий (ставки и продолжительности инвестиционного проекта).

Полученный таким образом равномерный поток той же продолжительности будет гарантированно иметь совпадающее значение NPV. Следовательно, выполнится одно из условий возникновения финансовой эквивалентности – равенство результатов. Но из аннуитетного потока всегда можно получить и ставку внутренней доходности, и любые значения сроков окупаемости (простой, дисконтированный, точный).

Недостатком предложенного метода можно считать необходимость точного знания процентной ставки, поскольку операция приведения при ином ее уровне изменит получаемые параметры аннуитета и дальнейшей его оценки. Не совпадут оценки будущей стоимости начального и эквивалентного потоков. А главное – внутренняя доходность определится как функция заданного уровня цены денежных ресурсов. По своему теоретическому содержанию она – производная структуры cash flow и поэтому может исполнять роль критерия, с которым и сравнивается реальная процентная ставка.

Оценка потоков, данные которых сведены в табл. 5.5, при ставке, равной 10%, дает следующие результаты:

Табл. 5.6

Оценки неординарных денежных потоков, полученные путем преобразования к эквивалентному аннуитету

Показатель	Поток А	Поток В
Величина приведенных затрат	-9562,33	-11660,40
Величина приведенных доходов (PVA)	20714,73	16310,57
NPV проекта при ставке 10%	11152,41	4650,17
CRF при ставке 10%	0,162745	0,162745
Размер взноса эквивалентного аннуитета (PMT)	3371,23	2654,47
IRR аннуитетного потока*	33,26%	18,65%
Простой срок окупаемости PP	3 года	5 лет
Дисконтированный срок окупаемости DPP	4 года	7 лет
Точное значение срока окупаемости по формуле 5.19	3,5 года	6,07 лет

* Говорить о доходности на уровне 86% и даже 160%, очевидно, преждевременно.

В силу названных недостатков приведенная методика носит рекомендательный характер и может рассматриваться, как вспомогательная для целей анализа инвестиций, генерирующих неординарный денежный поток.

Задачу оценки инвестиций, критерии эффективности которых не определяются по традиционной методике, нужно решать, исходя из условия, что внутренняя доходность всегда существует. Причем, определяется этот критерий не только конфигурацией денежного потока, но и теми условиями, в рамках действия которых оценивается инвестиционный проект. Абсолютная оценка эффективности не может не зависеть от реальной стоимости денежных ресурсов. Относительный показатель получается из абсолютного.

Если инвестиция единственная, ситуация отсутствия IRR возникнуть в принципе не может. Зависимость NPV(r) всегда монотонно убывающая. Проекты, начавшиеся с притоков средств, собственно, и не имеют IRR, поскольку первая положительная компонента не дисконтируется и при любой ставке сохраняет NPV положительным. Но, с позиций здравой логики, этот «доход» – не благо, а долг, который копится на протяжении всего периода реализации проекта.

Наличие в структуре неординарного потока нескольких или даже многих инвестиций (расходов, вложений) позволяет предполагать, что сама оценка (приведение) должно осуществляться не к начальному моменту, как полагается в традиционной методике, а к моменту осуществления последней инвестиции. Весь срок реализации проекта может, таким образом, быть разделен на две части: период до окончания вливаний в проект и следующий за ним интервал, на котором осуществляется исключительно отдача от вложений. (рис. 22). Отметим, что второго периода может и не существовать, если проект завершается оттоком капитала (таковы, например, рассмотренные выше проекты из табл. 5.5).

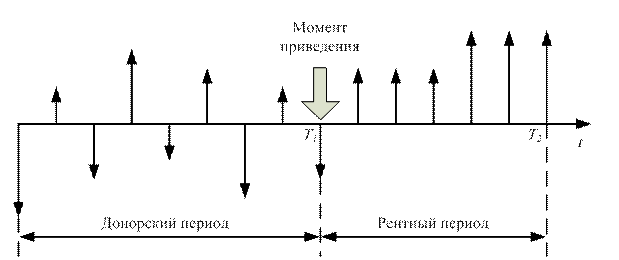
Рис. 22 Приведение неординарного потока

На первом этапе происходит собственно преобразование ресурсов в затраты. Даже те доходы, которые генерируются самим проектом, а не привносятся со стороны, направляются на последующие вложения. Это не доходы, а заимствованные ресурсы для вливаний. Этот этап на рисунке условно назван «донорским».

Второй этап характеризует «рентный» период. Положительные cash flow этого периода окупают собой инвестиции, не окупившиеся ранее, а также формируют привнесенный проектом финансовый потенциал.

Доходы рентного периода поступают в ту же финансовую среду, из которой поступили донорские вложения. Поэтому все положительные потоки имеют в проекте цену, выраженную реальной процентной ставкой. Отрицательные потоки (собственно инвестиции) работают в проекте с некоторой эффективностью, которую и требуется найти.

IRE – Internal Rate of Efficiency – аналог IRR, внутренняя норма эффективности, ставка, характеризующая отдачу неординарного проекта и существующая независимо от структуры денежного потока, получается из следующей формулы:

(5.23)

Дисконтированная оценка потока, аналог NPV, условно названая Net Value of Investments (NVI) представляет собой разницу всех положительных и отрицательных компонент, приведенных к моменту осуществления последней инвестиции:

(5.24)

Отметим, что если вложение единственно, NVI превращается в NPV (T ₁=0), IRE преобразуется в IRR. Для любого (в т.ч. неординарного потока)

(5.25)

Таким образом, традиционная методика оценки денежных потоков представляет собой частный случай описанной выше.

IRE является функцией реальной процентной ставки и показывает, с какой эффективностью работали в проекте вложения. У эффективных проектов IRE>r. У неэффективных всегда меньше.

Из формулы 5.25, взаимосвязь NPV и NVI следующая:

Если NVI<0, проект убыточен и, соответственно, не окупается.

Ситуация NVI>0 характеризует эффективные проекты. Сам критерий NVI характеризует своим значением абсолютно реальный вклад проекта в финансовый потенциал инвестора[3]. Это ценность суммы, далее работающей на покрытие осуществленных вложений в течение срока окупаемости, приведенная к моменту T₁. Для оценки сроков окупаемости эффективных проектов целесообразно сравнивать NVI с приведенной рентой (последний член формулы 5.24) либо с сальдо приведенных инвестиций. Для удобства дальнейших выкладок введем следующие обозначения:

; ;

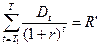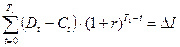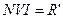, - уникальная ситуация, когда на момент T₁ окупились абсолютно все вложения. .

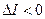, - на момент приведения существует отрицательное сальдо не окупившихся вложений, на покрытие которых работает полученный финансовый потенциал в течение некоторого времени после момента Т ₁.

; ;

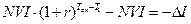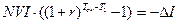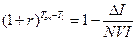
; (5.26)

Напомним, что формула срока окупаемости должна содержать логарифм. 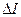подставляется в формулу отрицательным.

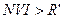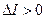, - случай, когда последние инвестиции осуществляются, по сути, уже окупившись за счет доходов от предшествующих вложений. 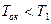. Определить его точнее можно только из пошагового анализа денежных потоков проекта.

Результат оценки уже рассмотренных неординарных потоков по описанной методике представлен в табл. 5.7. Примечательно, что они почти идентичны полученным по методике построения финансово эквивалентного аннуитета (см. табл. 5.6)

Табл. 5.7

Оценки неординарных денежных потоков, полученные путем расчета NVI и IRE

Показатель	Поток А	Поток В
NPV при ставке 10%	11152,41	4650,17
IRR	Не существует	86,2% и 161,6%
T1, лет
NVI при ставке 10%	28926,47	12061,33
IRE при ставке 10%	30,14%	17,43%
Доходность финансово эквивалентного аннуитета (табл. 5.6)	33,26%	18,65%
Срок окупаемости, лет	2,63 года	6,9 лет
Tок финансово эквивалентного аннуитета (табл. 5.6)	3,5 года	6,07 лет
DPP финансово эквивалентного аннуитета (табл. 5.6)	4 года	7,0 лет

Дополним представленные материалы данными оценки потока, имеющего и «донорский», и «рентный период».

Табл. 5.8

Неординарный поток с рентным периодом и результаты его оценки

Поток	Периоды
С		-4000				-3000	-2000
Показатель	Поток С
NPV при ставке 10%	636,771
IRR	Не существует
«Донорский» период T1, лет
«Рентный» период T2, лет
NVI при ставке 10%	1128,079
IRE при ставке 10%	13,31%
	2467,386
	10402,73
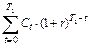
	11742,04
	-1339,31
Срок окупаемости, лет	14,2 года

Дата добавления: 2014-12-27