
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЗАНЯТИЕ 9. Определители n-го порядка: свойства определителей и способы вычисления
Прочти, реши и опять прочти!..
Настоящее методическое пособие предназначено помочь студентам в освоении теоретических вопросов предмета «Линейная алгебра» путём использования подробно решённых задач и примеров.
Одновременно, пособие должно помочь наиболее мотивированным студентам развивать навыки самостоятельной работы, что очень важно при подготовке инженера любой специальности.
Тем, кто захочет воспользоваться возможностью показать себя постоянно и эффективно работающим, привлечь к себе внимание преподавателей и научных руководителей, приобрести авторитет среди своих товарищей, пособие тоже окажет помощь.
Рассмотренные и доступные с самого начала семестра материалы помогут качественно готовиться и к лекциям, и практическим занятиям, и к различным контрольным испытаниям.
СОДЕРЖАНИЕ:
| № | Тема занятия: | Стр. |
| 9. | Определители n-го порядка: свойства определителей и способы вычисления. | |
| 10. | Линейные операции с матрицами: умножение на число и сложение матриц. Произведение матриц. Вырожденные матрицы. Определитель произведения квадратных матриц. | |
| 11. | Обратная матрица: определение, способы вычисления. Матричные уравнения и способы их решения. | |
| 12. | Линейное пространство n-векторов. Линейная зависимость n-векторов. Определения ранга матрицы и его вычисление для совокупности векторов и матрицы. | |
| 13. | Неоднородные системы уравнений. Решение системы уравнений методом Гаусса и по правилу Крамера. | |
| 14. | Неоднородные системы уравнений. Общее решение систем уравнений с использованием теоремы Кронекера-Капелли. | |
| 15. | Однородные системы уравнений. Общее решение системы уравнений, Фундаментальная система решений. Связь решения неоднородной системы уравнений и соответствующей ей однородной системы. | |
| 16. | Контрольная работа №2. Прием части-2 БДЗ. | |
| 17. | Систематизация материала по всем темам Занятий 1-16. О подготовке к экзамену. |
•◄●►•
Замечание: если в рассматриваемом Задании пример имеет номер 9-5, это значит, что в Задании 9 пример имеет номер по порядку 5.
☺ ☻ ☺
Пример 9–1: Разлагая определитель по 2-му столбцу, вычислить: 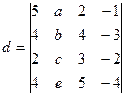 .
.
Решение:
Замечание: удобно вынести множитель 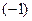 из столбца-4, и только потом применять разложение по столбцу!
из столбца-4, и только потом применять разложение по столбцу!
1) Запишем: – d = a 
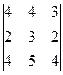 + b
+ b 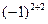
 + c
+ c 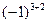
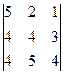 +e
+e 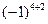
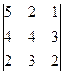 ,
,
или: d = 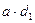 –
– 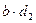 +
+ 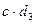 –
– 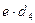 .
.
2) Вычислим все определители разложения: 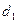 = (1) =
= (1) = 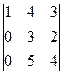 = (2) =
= (2) =  =2.
=2.
Операции: (1): [C1]–[C3]. (2): применяем разложение определителя по столбцу-1 и завершаем вычисление.
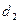 = (1) =
= (1) = 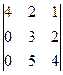 = (2) =4·
= (2) =4· 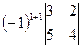 =8.
=8.
Операции: (1): [C1]–[C3]. (2): применяем разложение определителя по столбцу-2 и завершаем вычисление.
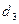 = (1) =
= (1) =  = (2) =
= (2) = 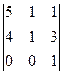 =1·
=1·  =1.
=1.
Операции: (1): [R3]–[R2];. (2): [C1]–[C3]. (3): применяем разложение определителя по строке-3 и завершаем вычисление.
 = (1) =
= (1) = 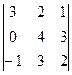 = (2) =
= (2) = 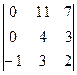 = (3) =–1
= (3) =–1 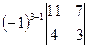 =–5.
=–5.
Операции: (1): [C1]–[C2]. (2): [R1]+[R3]·3. (3): применяем разложение определителя по столбцу-1 и завершаем вычисление.
3) Окончательно имеем: 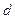 =
= 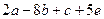 .
.
Ответ: d = 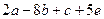 .
.
Пример 9–2: Вычислить определитель: 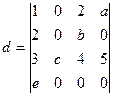 .
.
Решение:
Воспользуемся свойствами определителя и вычислим:
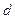 = (1) = – e ·
= (1) = – e ·  = (2) =–
= (2) =– 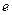 ·
· 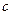
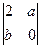 =
=  .
.
Операции: (1): применим разложение определителя по строке-4. (2): применяем разложение по столбцу-1 и завершаем вычисление.
Ответ:  .
.
Пример 9–3: Вычислить определитель: 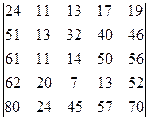 разложением по строке (столбцу).
разложением по строке (столбцу).
Решение:
Применяя операции со строками и столбцами, добьёмся максимальной простоты чисел-элементов определителя:
d = (1) = 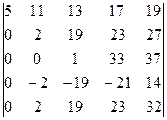 = (2) =10·
= (2) =10· 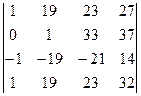 = (3) =10·
= (3) =10· 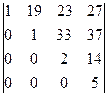 =100.
=100.
Операции: (1): [C1]–[C5]; [R2]–[R1]; [R3]–[R1]; [R4]–[R1]·2; [R5]–[R1]·2. (2): применяем разложение определителя по столбцу-1, вынося множитель 2 из получающегося определителя 4-го порядка. (3): [R3]+[R1]; [R4]–[R1]. (4): получен определитель треугольного вида → завершаем вычисление.
Ответ: d =100.
Пример 9–4: Вычислить определитель: 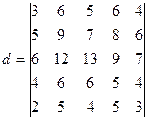 .
.
Решение:
1) Запишем: d = (1) = 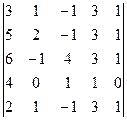 = (2) =
= (2) = 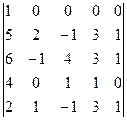 = (3) =
= (3) =  = (4) =
= (4) =
= 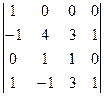 = (5) =
= (5) =  =5.
=5.
Операции: (1): [C2]–[C3]; [C2]–[C3]; [C4]–[C1]; [C3]–[C4]. (2): [R1]–[R5]. (3): применяем разложение определителя по строке-1. (4): [R1]–[R4]. (5): применяем разложение определителя по строке-1; [R1]–[R3] и завершаем вычисление.
Ответ: d =5.
Пример 9–5: Вычислить определитель: d= 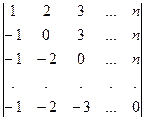 .
.
Решение:
Используя свойства определителя, выполним действия:
1) Прибавим 1-ю строку к 2-й, 3-й, и т.д. строкам → получен определитель треугольного вида с элементами на главной диагонали 1, 2, 3, …, n;
2) Известно, что такой определитель равен произведению элементов расположенных на главной диагонали: 1·2·3· … · n = n!
Ответ: d = n!
☻
Вопросы для самопроверки:
1. Может ли определитель n -го порядка не быть числом?
2. Изменится ли определитель n -го порядка, если в нем строки заменить столбцами и наоборот?
3. Изменится ли определитель n -го порядка, если в нем строки (или столбцы) поменять местами?
4. Изменится ли определитель n -го порядка, если в нем из одной строки вычесть другую строку?
5. Изменится ли определитель n -го порядка, если в нем из одного столбца вычесть другой столбец?
6. Изменится ли определитель n -го порядка, если в нем строку умножить на число?
7. Применение теоремы Лапласа предполагает уменьшение трудоемкости вычисления определителей высокого порядка?
Задачи для самоподготовки:
Пример C9 – 1: Разлагая определитель по 3-й строке, вычислить: 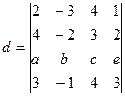 .
.
Ответ:d = 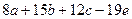 .
.
Пример C9 – 2: Вычислить определитель:  .
.
Ответ:  .
.
Пример C9 – 3: Вычислить определитель: 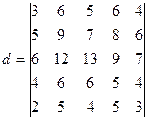 .
.
Ответ:d =5.
Пример C9 – 4: Вычислить определитель: 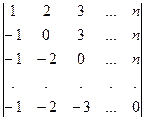 .
.
Ответ:d = n!.
< * * * * * >
|
|
Дата добавления: 2014-12-27; Просмотров: 645; Нарушение авторских прав?; Мы поможем в написании вашей работы!