Аналитическая геометрия. ЗАНЯТИЕ 17. Систематизация материала по всем темам Занятий 1-16

ЗАНЯТИЕ 17. Систематизация материала по всем темам Занятий 1-16. Особенности подготовки к экзамену.

☺ ☻ ☺

Преподаватель сообщает студентам о том, как будет организован экзамен, каковы требования для успешной сдачи экзамена. Беседа может включать также обсуждение особенностей психологической подготовки к экзамену!

Вопросы для подготовки к экзамену по курсу «Линейная алгебра»:

1. Определение и правила построения систем координат на прямой, на плоскости и в пространстве.

2. Схема построения полярных координат на плоскости - M(ρ,φ); цилиндрических координат - M(ρ,φ,z) в пространстве; сферических координат - M(ρ,φ,θ) в пространстве.

3. Определение геометрического вектора, вычисление его длины (модуля) для случаев задания: начальной M ₁ (x ₁, y ₁, z ₁) и конечной M ₂ (x ₂, y ₂, z ₂) точками; в виде .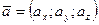

4. Геометрический смысл линейных операций с векторами: сумма векторов и 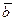(правила «параллелограмма» и «треугольника»); умножение вектора на вещественное число λ.

5. Определение линейной зависимости и базиса для векторов: на плоскости; в пространстве.

6. Сложение векторов и 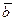, заданных в координатной форме, умножение вектора , заданного в координатной форме, на вещественное число .

7. Определение, физический смысл и основные свойства скалярного произведения векторов и 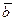. 8. Способы вычисление скалярного произведения.

9. Определение, физический смысл и основные свойства векторного произведения векторов и 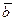. 10. Способы вычисление векторного произведения.

11. Определение и вычисление смешанного произведения векторов , 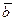и .

12. Общее уравнение прямой на плоскости, нормирование уравнения прямой.

13. Вычисления: угла между двумя прямыми и расстояния от точки до прямой.

14. Общее уравнение плоскости, нормирование уравнения плоскости.

15. Вычисления: угла между двумя плоскостями и расстояния от точки до плоскости.

16. Каноническое уравнение прямой в пространстве.

17. Вычисления: угла между прямой и плоскостью; расстояния от точки до прямой в пространстве, расстояния между двумя прямыми в пространстве.

18. Определение и основные свойства эллипса, гиперболы и параболы. Эксцентриситет, директриса кривой 2-го порядка.

19. Поверхности 2-го порядка, их получение путем вращения вокруг осей OX, OY, OZ кривых 2-го порядка.

20. Эскизы поверхностей: эллипсоида, двуполостного и однополостного гиперболоидов, параболоида, конуса, цилиндра, гиперболического параболоида.

Дата добавления: 2014-12-27