
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЗАНЯТИЕ 14. Неоднородные системы уравнений. Общее решение систем уравнений с использованием теоремы Кронекера-Капелли
|
|
|
|
☺ ☻ ☺
Практическое использование теоремы Кронекера–Капелли при решении произвольной системы уравнений. Общая схема решения:
A 1 *: Вычисляем ранги: 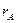 и
и 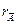 для матриц
для матриц 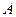 и
и 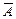 . Если:
. Если: 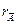
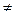
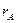 , то система решений не имеет. Пусть
, то система решений не имеет. Пусть 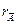 =
= 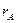 =
= 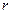 . Это значит, что определился общий для матриц
. Это значит, что определился общий для матриц 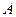 и
и 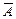 базовый минор: M
базовый минор: M 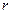 . На этот минор будем ссылаться при построении общей схемы решения системы.
. На этот минор будем ссылаться при построении общей схемы решения системы.
Замечание: в случае, когда система не имеет решений, учащийся доволен: задание уже выполнено; для специалиста возникшая ситуация сигналит о том, что наблюдение за процессом было некорректным при создании конкретного уравнения-модели и его нельзя учитывать!
A 2 *: В системе уравнений оставляем только те 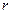 уравнения-строки, которые попали в базовый минор: остальные являются следствием выделенных.
уравнения-строки, которые попали в базовый минор: остальные являются следствием выделенных.
Замечание: помня, что каждое уравнение системы имеет для специалиста особый смысл, стремятся так реализовать алгоритм выделения базового минора, чтобы наиболее интересные для специалиста уравнения попали в базовый минор!
A 3 *: В левой части каждого из оставшихся для дальнейшего решения уравнений оставляем те 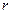 столбцов с неизвестными, которые попали в базовый минор: остальные неизвестные объявляем свободными и соответствующие столбцы с ними переносим в правую часть.
столбцов с неизвестными, которые попали в базовый минор: остальные неизвестные объявляем свободными и соответствующие столбцы с ними переносим в правую часть.
Замечание: процесс объявления некоторых неизвестных свободными для специалиста не является случайным: это варьируемые параметры процесса, при помощи которых можно выделять наиболее желательные реализации процесса!
A 4 *: Находим решения преобразованной системы уравнений, применяя формулы Крамера: определитель преобразованной системы не равен нулю!
A 5 *: Полученное решение системы называют общим: вычисленные по формулам Крамера неизвестные выражаются через свободные неизвестные. Присваивая свободным неизвестным произвольные значения, получаем частные решения.
Замечание: отметим ещё раз, что свободных неизвестных 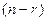 : их можно воспринимать как число степеней свободы процесса; вычисляемых неизвестных –
: их можно воспринимать как число степеней свободы процесса; вычисляемых неизвестных – 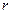 .
.
••• ≡ •••
Пример 14 – 1: Исследовать систему уравнений:  Найти общее решение и одно частное.
Найти общее решение и одно частное.
Решение:
1). Составим матрицы: 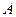 =
= 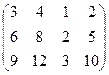 ,
, 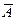 =
=  .
.
2). Найдем ранги матриц 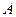 и
и 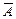 . Начнём с матрицы системы
. Начнём с матрицы системы 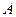 . Не равных нулю миноров 2-го порядка несколько. Это значит, что
. Не равных нулю миноров 2-го порядка несколько. Это значит, что 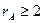 . Выделим для окаймления минор (не равен нулю), расположенный в правом верхнем углу матрицы
. Выделим для окаймления минор (не равен нулю), расположенный в правом верхнем углу матрицы 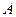 :
:
3). Окаймляющие миноры будем обозначать: 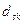 , где
, где 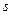 – указывает номер отмеченной для окаймления строки,
– указывает номер отмеченной для окаймления строки, 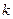 – указывает номер отмеченного для окаймления столбца. Тогда можем записать:
– указывает номер отмеченного для окаймления столбца. Тогда можем записать:
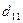 =
= 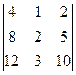 =4·
=4· 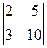 –8·
–8· 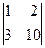 +12·
+12· 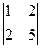 = m 1· (5) – h 1· (4) + g 1· (1) =4·(5)–8·(4)+12·(1) =0;
= m 1· (5) – h 1· (4) + g 1· (1) =4·(5)–8·(4)+12·(1) =0;
Замечание: параметры: m 1, h 1, g 1 изменяются при переходе к минорам 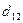 ,
, 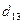 , числа: (5), (4), (1) не изменяются. Это позволяет применить единый шаблон вычислений!
, числа: (5), (4), (1) не изменяются. Это позволяет применить единый шаблон вычислений!
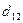 =
= 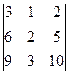 = m 2· (5) – h 2· (4) + g 2· (1) = 3·(5)–6·(4)+9·(1) =0;
= m 2· (5) – h 2· (4) + g 2· (1) = 3·(5)–6·(4)+9·(1) =0;
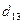 =
= 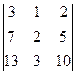 = m 3· (5) – h 3· (4) + g 3· (1) = 3·(5)–7·(4)+13·(1) =0.
= m 3· (5) – h 3· (4) + g 3· (1) = 3·(5)–7·(4)+13·(1) =0.
4). Так как все миноры 3-го порядка оказались равными нулю, то 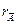 =
= 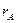 =2. Это значит – система совместна.
=2. Это значит – система совместна.
5). Учитывая расположение не равного нулю минора, 3-е уравнение отбрасываем и свободными неизвестными объявляем 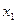 и
и 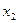 :
:

далее применяем правило Крамера:
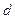 =1;
=1; 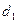 =
=  =
= 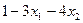 ;
; 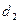 =
= 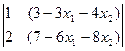 =1.
=1.
6). Общее решение системы: 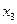 =
= 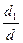 =
= 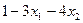 ;
;  =
= 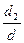 =1; частное решение получим при значениях:
=1; частное решение получим при значениях: 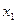 =–1,
=–1, 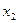 =1, →
=1, → 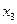 =0,
=0,  =1.
=1.
Ответ: общее решение: 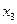 =
= 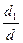 =
= 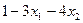 ;
;  =
= 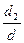 =1; частное решение: (–1,1,0,1).
=1; частное решение: (–1,1,0,1).
Пример 14 – 2: Исследовать систему уравнений:  Найти общее решение и одно частное.
Найти общее решение и одно частное.
Решение:
1). Составим матрицы: 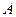 =
=  ,
, 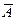 =
=  .
.
2). Найдем ранги матриц 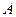 и
и 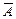 . Начнём с матрицы системы
. Начнём с матрицы системы 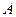 . Не равных нулю миноров 2-го порядка несколько. Это значит, что
. Не равных нулю миноров 2-го порядка несколько. Это значит, что 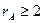 . Выделим для окаймления минор (не равен нулю), расположенный в правом верхнем углу матрицы
. Выделим для окаймления минор (не равен нулю), расположенный в правом верхнем углу матрицы 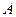 :
:
| -2 | |||||
| -4 | |||||
| -6 | |||||
3). Окаймляющие миноры будем обозначать: 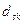 , где
, где 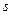 – указывает номер отмеченной для окаймления строки,
– указывает номер отмеченной для окаймления строки, 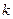 – указывает номер отмеченного для окаймления столбца. Тогда можем записать:
– указывает номер отмеченного для окаймления столбца. Тогда можем записать:
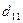 =
= 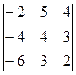 =(–2)·
=(–2)·  –(–4)·
–(–4)· 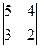 +(–6)·
+(–6)· 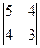 = m 1· (–1) – h 1· (–2) + g 1· (–1) =
= m 1· (–1) – h 1· (–2) + g 1· (–1) =
= (–2)·(–1)–(–4)·(–2)+(–6)·(–1)=0;
Замечание: параметры: m 1, h 1, g 1 изменяются при переходе к минорам 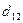 ,
, 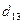 , числа: (–1), (–2), (–1) не изменяются. Это позволяет применить единый шаблон вычислений!
, числа: (–1), (–2), (–1) не изменяются. Это позволяет применить единый шаблон вычислений!
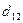 =
=  = m 2· (–1) – h 2· (–2) + g 2· (–1) =3·(–1)–6·(–2)+9·(–1)=0;
= m 2· (–1) – h 2· (–2) + g 2· (–1) =3·(–1)–6·(–2)+9·(–1)=0;
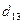 =
=  = m 3· (–1) – h 3· (–2) + g 3· (–1) = 2·(–1)–3·(–2)+4·(–1)=0.
= m 3· (–1) – h 3· (–2) + g 3· (–1) = 2·(–1)–3·(–2)+4·(–1)=0.
4). Так как все миноры 3-го порядка оказались равными нулю, то 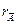 =
= 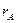 =2. Это значит – система совместна.
=2. Это значит – система совместна.
5). Учитывая расположение не равного нулю минора, 3-е уравнение отбрасываем и свободными неизвестными объявляем 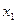 и
и 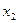 :
:

далее применяем правило Крамера:
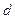 =–1;
=–1; 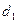 =
=  =
= 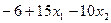 ;
; 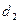 =
=  =
=  .
.
6). Общее решение системы 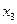 =
= 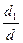 =
=  ,
,  =
= 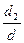 =
=  , частное решение получим при значениях:
, частное решение получим при значениях: 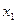 =
= 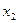 =1, →
=1, → 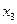 =1,
=1,  =–1.
=–1.
Ответ: общее решение системы 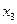 =
= 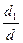 =
=  ,
,  =
= 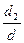 =
=  ; частное: (1,1,1,–1).
; частное: (1,1,1,–1).
Пример 14 – 3: Исследовать систему: 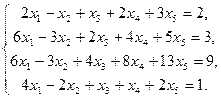 Найти общее и частное решение.
Найти общее и частное решение.
Решение:
1). Составим матрицы: 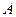 =
=  ,
, 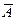 =
= 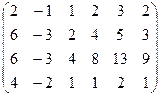 .
.
2). Найдем ранги матриц 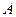 и
и 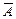 . Начнём с матрицы системы
. Начнём с матрицы системы 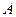 . Не равных нулю миноров 2-го порядка несколько. Это значит, что
. Не равных нулю миноров 2-го порядка несколько. Это значит, что 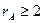 . Выделим для окаймления минор (не равен нулю), расположенный в правом верхнем углу матрицы
. Выделим для окаймления минор (не равен нулю), расположенный в правом верхнем углу матрицы 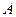 :
:
| -1 | ||||||
| -3 | ||||||
| -3 | ||||||
| -2 | ||||||
3). Окаймляющие миноры будем обозначать: 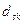 , где
, где 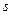 – указывает номер отмеченной для окаймления строки,
– указывает номер отмеченной для окаймления строки, 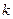 – указывает номер отмеченного для окаймления столбца.
– указывает номер отмеченного для окаймления столбца.
Замечание: догадываемся, что после вычисления 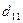 не нужно переходить к вычислению миноров
не нужно переходить к вычислению миноров 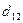 ,
, 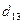 ,
, 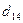 , а вычислить раньше минор
, а вычислить раньше минор  .
.
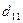 =
= 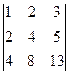 =4·
=4·  –8·
–8· 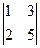 +13·
+13·  = m 1· (–2) – h 1· (–1) + g 1· (0) =
= m 1· (–2) – h 1· (–1) + g 1· (0) =
=4·(–2)–8·(–1)+13·(0)=0.
Замечание: параметры: m 1, h 1, g 1 изменяются при переходе к минору  , числа: (–2), (–1), (0) не изменяются. Это позволяет применить единый шаблон вычислений!
, числа: (–2), (–1), (0) не изменяются. Это позволяет применить единый шаблон вычислений!
 =
= 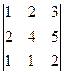 = m 2· (–2) – h 2· (–1) + g 2· (0) =1·(–2)–1·(–1)+2·(0) = –1≠0.
= m 2· (–2) – h 2· (–1) + g 2· (0) =1·(–2)–1·(–1)+2·(0) = –1≠0.
4). Интуиция сработала! Так как  ≠0, то теперь будем окаймлять этот минор и вычислять окаймляющие миноры. Для удобства поменяем местами строки 3 и 4:
≠0, то теперь будем окаймлять этот минор и вычислять окаймляющие миноры. Для удобства поменяем местами строки 3 и 4:
| -1 | ||||||
| -3 | ||||||
| -2 | ||||||
| -3 | ||||||
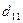 =
= 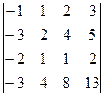 =(–1)·
=(–1)·  –(–3)·
–(–3)· 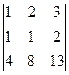 +(–2)·
+(–2)· 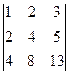 – (–3)·
– (–3)· 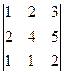 ,
,
или: 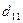 = m 1· (–6) – h 1· (–1) + g 1· (0) – q 1· (–1) =(–1)·(–6)–(–3)·(–1)+(–2)·(0)–(–3)·(–1) =0;
= m 1· (–6) – h 1· (–1) + g 1· (0) – q 1· (–1) =(–1)·(–6)–(–3)·(–1)+(–2)·(0)–(–3)·(–1) =0;
Замечание: параметры: m 1, h 1, g 1 изменяются при переходе к минорам 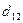 ,
, 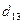 , числа: (–12), (14), (0), (–2) не изменяются. Это позволяет применить единый шаблон вычислений!
, числа: (–12), (14), (0), (–2) не изменяются. Это позволяет применить единый шаблон вычислений!
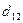 =
=  = m 2· (–6) – h 2· (–1) + g 2· (0) – q 2· (–1) = 2·(–6)–6·(–1)+4·(0)–6·(–1) =0;
= m 2· (–6) – h 2· (–1) + g 2· (0) – q 2· (–1) = 2·(–6)–6·(–1)+4·(0)–6·(–1) =0;
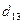 =
= 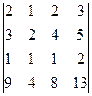 = m 3· (–6) – h 3· (–1) + g 3· (0) – q 3· (–1) = 2·(–6)–3·(–1)+1·(0)–9·(–1) =0.
= m 3· (–6) – h 3· (–1) + g 3· (0) – q 3· (–1) = 2·(–6)–3·(–1)+1·(0)–9·(–1) =0.
5). Следует: 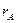 = 3. Учитывая расположение не равного нулю минора, 3-е уравнение отбрасываем и свободными неизвестными объявляем
= 3. Учитывая расположение не равного нулю минора, 3-е уравнение отбрасываем и свободными неизвестными объявляем 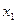 и
и 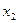 :
:
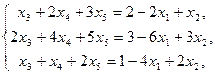
далее применяем правило Крамера, учитывая, что определитель системы равен 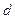 =–1:
=–1:
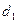 =
=  =
=  =
=  ;
;
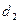 =
= 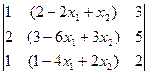 =
= 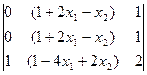 =0;
=0;
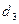 =
=  =
=  =–
=–  .
.
6). Общее решение системы: 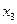 =
= 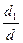 =
=  ;
;  =
= 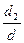 =0;
=0; 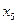 =
=  =
=  ; частное решение получим при значениях:
; частное решение получим при значениях: 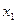 =1,
=1, 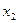 =2, →
=2, → 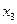 =–1,
=–1,  =0,
=0, 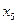 =1.
=1.
Ответ: общее решение: 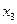 =
= 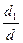 =
=  ;
;  =
= 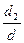 =0;
=0; 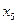 =
=  =
=  ; частное: (1,2,–1,0,1).
; частное: (1,2,–1,0,1).
Пример 14 – 4: Исследовать систему уравнений:  Найти общее решение и одно частное.
Найти общее решение и одно частное.
Решение:
1). Составим матрицы: 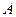 =
=  ,
, 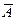 =
=  .
.
2). Найдем ранги матриц 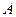 и
и 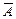 . Начнём с матрицы системы
. Начнём с матрицы системы 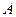 . Не равных нулю миноров 2-го порядка несколько. Это значит, что
. Не равных нулю миноров 2-го порядка несколько. Это значит, что 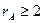 . Выделим для окаймления минор (не равен нулю), расположенный в левом верхнем углу матрицы
. Выделим для окаймления минор (не равен нулю), расположенный в левом верхнем углу матрицы 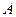 :
:
3). Окаймляющие миноры будем обозначать: 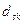 , где
, где 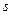 – указывает номер отмеченной для окаймления строки,
– указывает номер отмеченной для окаймления строки, 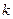 – указывает номер отмеченного для окаймления столбца. Тогда можем записать:
– указывает номер отмеченного для окаймления столбца. Тогда можем записать:
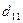 =
=  = 3
= 3 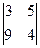 –2
–2 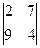 +1
+1  = m 1· (–33) – h 1· (–55) + g 1· (–11) =
= m 1· (–33) – h 1· (–55) + g 1· (–11) =
=3·(–33)–2·(–55)+1·(–11) =0;
Замечание: параметры: m 1, h 1, g 1 изменяются при переходе к минорам 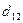 ,
, 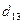 , числа: (–33), (–55), (–11) не изменяются. Это позволяет применить единый шаблон вычислений!
, числа: (–33), (–55), (–11) не изменяются. Это позволяет применить единый шаблон вычислений!
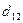 =
=  = m 2· (–33) – h 2· (–55) + g 2· (–11) = 1·(–33) –2·(–55)+7·(–11)=0;
= m 2· (–33) – h 2· (–55) + g 2· (–11) = 1·(–33) –2·(–55)+7·(–11)=0;
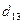 =
= 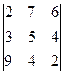 = m 3· (–33) – h 3· (–55) + g 3· (–11) = 6·(–33) –4·(–55)+2·(–11) =0.
= m 3· (–33) – h 3· (–55) + g 3· (–11) = 6·(–33) –4·(–55)+2·(–11) =0.
4). Следует: ранг матрицы 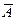 :
: 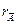 =2. Так как
=2. Так как 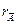 =
= 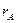 =2, то система совместна.
=2, то система совместна.
5). Учитывая расположение не равного нулю минора, 3-е уравнение отбрасываем и свободными неизвестными объявляем 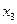 и
и  :
: 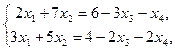
далее применяем правило Крамера:
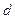 = – 11;
= – 11; 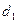 =
= 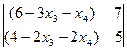 =
= 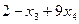 ;
; 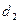 =
=  =
=  .
.
6). Запишем общее решение системы 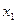 =
= 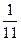
 ;
; 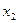 =
= 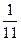
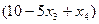 . Частное решение системы получим при значениях:
. Частное решение системы получим при значениях: 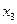 =0,
=0,  = 1 →
= 1 → 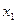 = –1,
= –1, 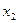 = 1.
= 1.
Ответ: общее решение системы 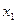 =
= 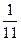
 ,
, 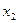 =
= 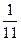
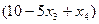 ; частное решение: (–1,1,0,1).
; частное решение: (–1,1,0,1).
☻
Вопросы для самопроверки:
1. Как практически применяется теорема Кронекера-Капелли при решении системы линейных уравнений?
2. Можно ли провести полное исследование системы уравнений без использования теоремы Кронекера-Капелли?
3. Может ли ранг расширенной матрицы 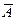 быть равным 7, а ранг А -матрицы 8? а наоборот?
быть равным 7, а ранг А -матрицы 8? а наоборот?
4. Могут ли ранги матриц А и 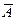 равняться нулю?
равняться нулю?
Задачи для самоподготовки:
Пример C14 – 1: Исследовать совместность и найти общее решение системы линейных уравнений в зависимости от значения параметра  :
: 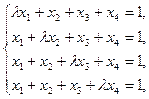
Ответ: система имеет бесчисленное множество решений, если  –1 = 0; если
–1 = 0; если  –1≠ 0, система имеет решение:
–1≠ 0, система имеет решение: 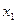 =
= 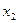 =
= 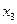 =
= 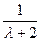 , откуда следует: если
, откуда следует: если  –2≠ 0, и не имеет решения при
–2≠ 0, и не имеет решения при  –2 = 0.
–2 = 0.
Пример C14 – 2: Исследовать систему уравнений:  Найти общее решение и одно частное.
Найти общее решение и одно частное.
Ответ: система несовместна → решений нет.
Пример C14 – 3: Исследовать совместность системы уравнений:  Найти общее решение этой системы.
Найти общее решение этой системы.
Ответ: x 1 = 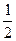 x 4 +
x 4 +  ; x 2 =
; x 2 = 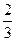 ; x 3 = –
; x 3 = – 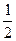 x 4 –
x 4 – 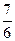 .
.
< * * * * * >
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 519; Нарушение авторских прав?; Мы поможем в написании вашей работы!