Переход к задаче линейного программирования для поиска смешанной стратегии Плательщика и цены игры

Шаг № 1. Для каждой стратегии Получателя Ai (в платежной матрице ей соответствует строка с номером i) запишем требование: при применении Плательщиком его смешанной стратегии средняя величина платежа должна оказаться не больше, чем цена игры n (количество таких неравенств совпадает с количеством строк в платежной матрице)

a_{i 1} y ₁ + a_{i 2} y ₂ +...+ a_iny_n £ n.

Если фактически, по результатам решения, будет осуществляться неравенство, то такая стратегия оказывается невыгодной для Получателя и неактивной.

Шаг № 2. Разделим все полученные неравенства на цену игры n, вводя новые искомые величины через соотношение Y_j = y_j /n

a_{i 1} Y ₁ + a_{i 2} Y ₂ +... + a_inY_n £ 1, где i = 1... m.

Эти неравенства образуют систему ограничений в ЛП-задаче.

Замечание: матрица ЛП-задачи равна исходной платежной матрице, все свободные члены равны единице, знак неравенств ограничивает искомые величины «сверху».

Шаг № 3. Используем соотношение y ₁ + y ₂ +... + y_n =1, деля его на цену игры n и вводя новые искомые

Y ₁+ Y ₂+... Y_n = 1/n.

Так как цена игры n соответствует минимальному гарантированному среднему платежу, то обратная ей величина 1/n, может быть получена в результате максимизации соответствующего функционального выражения. Отсюда получаем целевую функцию ЛП-задачи

F=Y ₁ + Y ₂ +... + Y_n → max.

Замечание: все коэффициенты целевой функции равны единице. Для Плательщика ЛП-задача требует максимизации значения целевой функции при ограничениях «сверху» на значения искомых величин Y_j.

Шаг № 4. Решение ЛП-задачи. В результате решения становятся известными величины Y ₁, Y ₂, ..., + Y_n, F _max.

Шаг № 5. Возврат к «игровой» задаче осуществляется с помощью соотношений

n =1/ F _max(цена игры);

y_j = Y_j ×n, (все вероятности, с которыми Получатель применяет свои чистые стратегии).

Шаг № 6. Проверка результата.

Значения вероятностей – неотрицательные, их сумма y ₁ + y ₂ +…+ y_n = 1.

При рассмотрении каждой отдельно взятой стратегии Плательщика 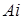должны выполняться неравенства, сформулированные при выполнении шага
№ 1, причем строгие неравенства указывают на невыгодные (неактивные) для Получателя стратегии, равенства – на активные стратегии, составляющие его смешанную стратегию

a_{i 1} y ₁ + a_{i 2} y ₂ +...+ a_iny_n £ n.

Значения цены игры n, полученные для Получателя и Плательщика, должны совпадать.

Пример 6б. Требуется найти смешанную стратегию Плательщика и цену игры, если дана платежная матрица (она получена в примерах 4а и 6а).

	В 2	В 3
А 1
А 2

Решение

1. Для каждой стратегии Получателя запишем требование: средняя величина платежа должна оказаться не больше, чем цена игры n

2. Разделим все полученные неравенства на цену игры n, вводя новые искомые величины через соотношение Y_j=y_j/ n

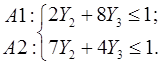
Эти неравенства образуют систему ограничений в ЛП-задаче. Матрица ЛП-задачи равна исходной платежной матрице.

3. Запишем целевую функцию ЛП-задачи

F = Y ₂ + Y ₃®max.

4. Пользуясь малым количеством искомых величин, решение ЛП-задачи проводим графическим методом. Линиям, ограничивающим область допустимых значений (по отдельность и для каждого неравенства системы), соответствуют строгие равенства, по которым найдем точки пересечения этих линий с координатными осями графика

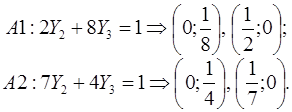
Выполним построение отрезков

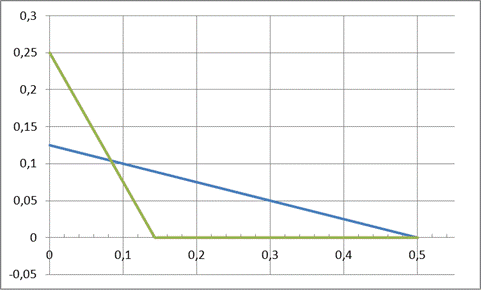
По результатам построения делаем вывод: наибольшее значение целевая функция принимает в точке М, которая является точкой пересечения отрезков, соответствующих стратегиям А 1 и А 2.

Проведем аналитический расчет координат точки М и значения целевой функции

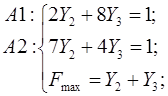
5. Возврат к «игровой» задаче осуществляется с помощью соотношений

n =1/ F _max=16/3» 5,33(цена игры);

y ₂ = Y ₂×n = 4/9» 0,44 (вероятность использования стратегии В 2);

y ₃ = Y ₃×n = 5/9» 0,56 (вероятность использования стратегии В 3).

6. Проверка результата.

Значения вероятностей – неотрицательные, их сумма y ₁ + y ₂ = 4/9 + 5/9 = 1.

При использовании Получателем его чистых стратегий рассчитаем среднюю величину платежа

Значение цены игры n, полученное для Плательщика, совпадает с результатом, полученным в примере 6а для Получателя.

Ответ

– Вероятности применения Плательщиком стратегий y ₂» 0,44 и y ₂» 0,56.

– Цена игры n» 5,33.

Дата добавления: 2014-12-27