
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Комплексное применение приемов при решении задач теории матричных игр с нулевой суммой 1 страница
|
|
|
|
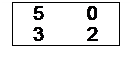
Пример 7. Для данной платежной матрицы:
- найти нижнюю и верхнюю цены игры;
- упростить данную платежную матрицу, исключив из неё доминируемые строки и столбцы, соответствующие заведомо невыгодным стратегиям игроков;
- выявить активные стратегии игроков графическим методом;
- найти решение игры: стратегии игроков и цену игры.
Решение:
1. Введем обозначения стратегий первого игрока (Получателя) и второго игрока (Плательщика):
| В1 | В2 | ||
| А1 | |||
| А2 |
2. В каждой строке выявим наименьшее значение, и из этих результатов – наибольшее:
| В1 | В2 | 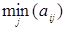
| |
| А1 | |||
| А2 |
Нижняя цена игры 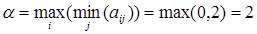 (реализуется при использовании Получателем стратегии А2).
(реализуется при использовании Получателем стратегии А2).
3. В каждом столбце выявим наибольшее значение, и из этих результатов – наименьшее:
| В1 | В2 | ||
| А1 | |||
| А2 | |||
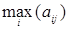
|
Верхняя цена игры 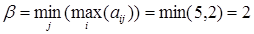 (реализуется при использовании Плательщиком стратегии В2).
(реализуется при использовании Плательщиком стратегии В2).
4. По результатам пп. 2,3 сделаем выводы: верхняя и нижняя цены игры совпадают, значит, игра имеет решение в чистых стратегиях (А2 и В2 для Получателя и Плательщика соответственно) и цена игры 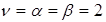 .[7]
.[7]
5. Для выявления доминируемых строк платежной матрицы проведем их поэлементное сравнение:
| В1 | В2 | ||
| А1 и А2 | 5>3 | 0<2 |
Вывод: знаки неравенств – разные, ни одной из строк исключить нельзя.
6. Для выявления доминируемых столбцов проведем их поэлементное сравнение:
| В1 и В2 | ||
| А1 | 5>0 | |
| А2 | 3>2 |
Вывод: знаки неравенств – одинаковые, значит, стратегия В2 доминирует стратегию В1 (стратегия В2, очевидно, более выгодна Плательщику) и стратегия В1 может быть исключена из платежной матрицы:
| В2 | ||
| А1 | ||
| А2 |
7. Вернемся к рассмотрению стратегий получателя. Очевидно, что для полученной в п. 6 платежной матрицы стратегия А2 доминирует стратегию А1, и последняя может быть исключена из платежной матрицы:
| В2 | ||
| А2 |
Дальнейшие упрощения невозможны.
8. По результатам пп. 5-7 сделаем вывод: путем последовательного упрощения платежная матрица сведена к единственному элементу. Он определяет решение игры: Получателем и Плательщиком используются стратегии А2 и В2, цена игры 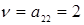 . Этот вывод полностью согласуется с результатами, полученными в п. 4.
. Этот вывод полностью согласуется с результатами, полученными в п. 4.
9. Проведем графическое сравнение стратегий Плательщика при разных смешанных стратегиях Получателя. Обозначим: x2 – частотность использования Получателем стратегии А2. Выполним графическое построение:


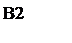
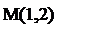
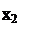

Здесь отрезок, соответствующий стратегии В1, соединяет величины платежа 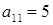 (при
(при 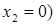 и
и 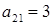 (при
(при 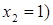 . Отрезок, соответствующий стратегии В2, соединяет величины платежа
. Отрезок, соответствующий стратегии В2, соединяет величины платежа 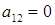 (при
(при 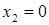 ) и
) и 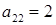 (при
(при 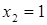 ).
).
Найдем такую точку М на нижней границе получившейся фигуры, которая наиболее удалена от оси абсцисс, и сделаем выводы:
- Так как отрезки на графике не пересекаются, то очевидно, что стратегия В2 более выгодна Плательщику при ЛЮБОМ выборе смешанной стратегии Получателем (этот вывод согласуется с результатами п.6). Она является единственной активной стратегией Плательщика.
- Точка М имеет координаты 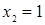 и
и 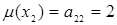 , – это указывает на использование Получателем только стратегии А2, при неактивной стратегии А1, и цене игры, совпадающей с одним из элементов платежной матрицы.
, – это указывает на использование Получателем только стратегии А2, при неактивной стратегии А1, и цене игры, совпадающей с одним из элементов платежной матрицы.
10. Проведем графическое сравнение стратегий Получателя при разных смешанных стратегиях Плательщика. Обозначим: 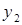 – частотность использования Плательщиком стратегии В2. Выполним графическое построение:
– частотность использования Плательщиком стратегии В2. Выполним графическое построение:

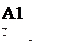
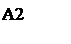
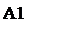
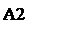
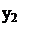
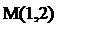
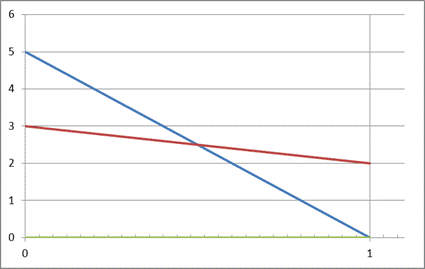
Здесь отрезок, соответствующий стратегии А1, соединяет величины платежа 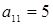 (при
(при 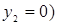 и
и 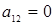 (при
(при 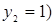 . Отрезок, соответствующий стратегии А2 соединяет величины платежа
. Отрезок, соответствующий стратегии А2 соединяет величины платежа 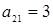 (при
(при 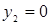 ) и
) и 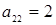 (при
(при 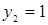 ).
).
Найдем точку М верхней границы получившейся фигуры, которая наиболее приближена к оси абсцисс и сделаем выводы:
- Так как отрезки, соответствующие стратегиям Получателя, пересекаются, выбор заведомо выгодной (доминирующей) стратегии сделать нельзя.
- Точка М находится не в точке пересечения отрезков, а связана ТОЛЬКО со стратегией Получателя А2, что указывает на использование Получателем только этой стратегии при неактивной стратегии А1.
- Верхняя граница фигуры, образованной пересекающимися отрезками, имеет точку, наиболее приближенную к оси абсцисс, при 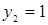 и
и 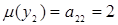 , – это указывает на использование Плательщиком только стратегии В2, при неактивной стратегии В1 и цене игры, совпадающей с одним из элементов платежной матрицы.
, – это указывает на использование Плательщиком только стратегии В2, при неактивной стратегии В1 и цене игры, совпадающей с одним из элементов платежной матрицы.
11. Сформулируем задачу линейного программирования для Получателя (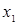 и
и 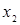 – искомые частотности использования стратегий А1 и А2,
– искомые частотности использования стратегий А1 и А2, 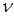 – искомая цена игры,
– искомая цена игры, 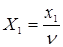 ,
, 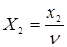 и
и 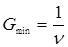 – «вспомогательные» ЛП-величины):
– «вспомогательные» ЛП-величины):
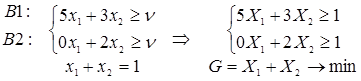
Задачу ЛП можно решить графическим методом. Выполним построения:
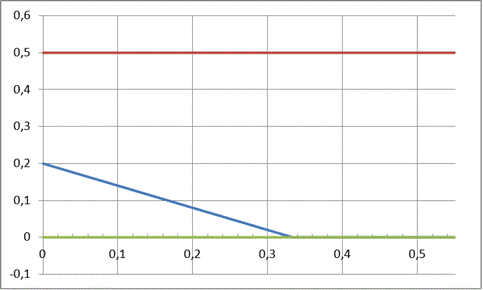
Найдем точку М, удовлетворяющую требованию минимизации целевой функции, и решение ЛП-задачи: 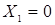 ,
, 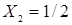 и
и 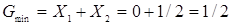 .
.
Решение исходной «игровой» задачи для Получателя находим, используя связи между искомыми и вспомогательными величинами:
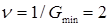 ,
, 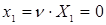 и
и 
Сделаем дополнительный вывод: Линия, соответствующая стратегии В1, целиком лежит под линией доминирующей стратегии В2, – это указывает на то, что актуальные ограничения возможных значений целевой функции связаны ТОЛЬКО со стратегией В2, которая является единственной активной стратегией Плательщика.
12. Решение задачи для Плательщика (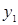 и
и 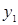 – частотности использования стратегий В1 и В2) найдем, используя следствия из ЛП -теорем двойственности и данных, полученных в предыдущем пункте:
– частотности использования стратегий В1 и В2) найдем, используя следствия из ЛП -теорем двойственности и данных, полученных в предыдущем пункте:
Так как 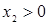 , для единственной активной стратегии А2 записываем точное равенство
, для единственной активной стратегии А2 записываем точное равенство 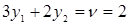 и рассматриваем его совместно с требованием
и рассматриваем его совместно с требованием 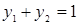 . Эту систему решаем, получая результат:
. Эту систему решаем, получая результат: 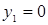 и
и 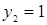 .
.
Ответ:
- Нижняя цена игры равна верхней цене игры (то есть игра имеет «седловую точку»): 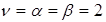 .
.
- Исключение доминируемых рядов из платежной матрицы сводит её к единственному элементу 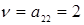 .
.
- Активные стратегии игроков – А2 для Получателя и В2 для Плательщика.
- Решение игры: 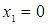 и
и 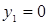 (стратегии А1 и В1 являются неактивными);
(стратегии А1 и В1 являются неактивными); 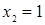 и
и 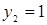 (Стратегии А2 и В2 используются игроками, как для однократного взаимодействия, так и во всех случаях многократного взаимодействия); цена игры
(Стратегии А2 и В2 используются игроками, как для однократного взаимодействия, так и во всех случаях многократного взаимодействия); цена игры 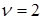 .
.
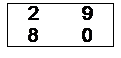 Пример 8. Для данной платежной матрицы:
Пример 8. Для данной платежной матрицы:
- найти нижнюю и верхнюю цены игры;
- упростить данную платежную матрицу, исключив из неё доминируемые строки и столбцы, соответствующие заведомо невыгодным стратегиям игроков;
- выявить активные стратегии игроков графическим методом;
- найти решение игры: стратегии игроков и цену игры.
Решение:
1. Введем обозначения стратегий первого игрока (Получателя) и второго игрока (Плательщика):
| В1 | В2 | ||
| А1 | |||
| А2 |
2. В каждой строке выявим наименьшее значение, и из этих результатов – наибольшее:
| В1 | В2 | 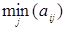
| |
| А1 | |||
| А2 |
Нижняя цена игры 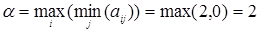 (реализуется при использовании Получателем стратегии А1).
(реализуется при использовании Получателем стратегии А1).
3. В каждом столбце выявим наибольшее значение, и из этих результатов – наименьшее:
| В1 | В2 | ||
| А1 | |||
| А2 | |||
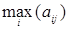
|
Верхняя цена игры 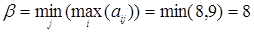 (реализуется при использовании Плательщиком стратегии В1).
(реализуется при использовании Плательщиком стратегии В1).
4. По результатам пп. 2,3 сделаем выводы: верхняя и нижняя цены игры не совпадают, значит, игра не имеет решения в чистых стратегиях (следует искать смешанную стратегию), и цена игры лежит в диапазоне 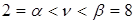 .
.
5. Для выявления доминируемых строк платежной матрицы проведем их поэлементное сравнение:
| В1 | В2 | ||
| А1 и А2 | 2<8 | 9>0 |
Вывод: знаки неравенств – разные, ни одной из строк исключить нельзя.
6. Для выявления доминируемых столбцов проведем их поэлементное сравнение:
| В1 и В2 | ||
| А1 | 2<9 | |
| А2 | 8>0 |
Вывод: знаки неравенств – разные, какой-либо столбец исключить нельзя.
7. По результатам пп. 5,6 сделаем выводы:
- Упрощение платежной матрицы (на основе явной выгодности одних стратегий по сравнению с альтернативными) невозможно.
- Путем последовательного упрощения платежной матрицы свести её к единственному элементу нельзя. Как обе стратегии Получателя, так и обе стратегии плательщика являются активными, а решение игры следует искать «в смешанных стратегиях». Этот вывод полностью согласуется с результатами, полученными в п. 4.
8. Так как множество активных стратегий обоих игроков выявлено, решение игры можно найти, строго приравнивая среднюю величину платежа цене игры[8]:
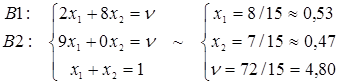
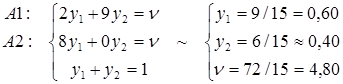
9. Проведем графическое сравнение стратегий Плательщика при разных смешанных стратегиях Получателя. Обозначим: 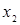 – частотность использования Получателем стратегии А2. Выполним графическое построение: отрезок, соответствующий стратегии В1, соединяет величины платежа
– частотность использования Получателем стратегии А2. Выполним графическое построение: отрезок, соответствующий стратегии В1, соединяет величины платежа 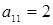 (при
(при 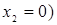 и
и 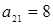 (при
(при 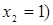 . Отрезок, соответствующий стратегии В2, соединяет величины платежа
. Отрезок, соответствующий стратегии В2, соединяет величины платежа 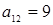 (при
(при  ) и
) и 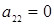 (при
(при 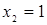 ).
).

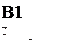
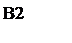

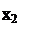

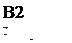
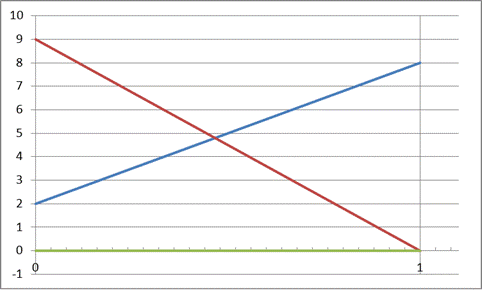
Найдем такую точку М на нижней границе получившейся фигуры, которая наиболее удалена от оси абсцисс, и сделаем выводы:
- Точка М имеет координаты 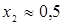 (то есть
(то есть 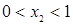 ) и
) и 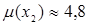 , – обе стратегии Получателя являются активными, позволяя ему достигать цену игры, превосходящую значение
, – обе стратегии Получателя являются активными, позволяя ему достигать цену игры, превосходящую значение 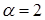 .
.
- Точка М соответствует пересечению отрезков, соответствующих стратегиям Плательщика В1 и В2, –это говорит о том, что обе эти стратегии являются активными.
10. Проведем графическое сравнение стратегий Получателя при разных смешанных стратегиях Плательщика. Обозначим: 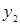 – частотность использования Плательщиком стратегии В2. Выполним графическое построение:
– частотность использования Плательщиком стратегии В2. Выполним графическое построение:

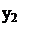

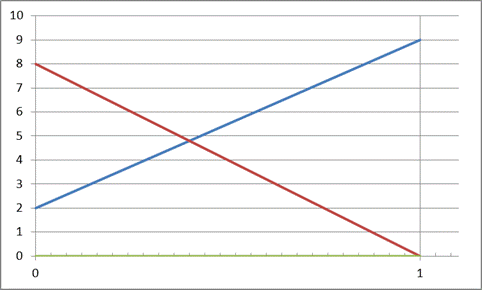
Здесь отрезок, соответствующий стратегии А1, соединяет величины платежа 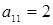 (при
(при 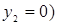 и
и 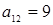 (при
(при 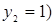 . Отрезок, соответствующий стратегии А2 соединяет величины платежа
. Отрезок, соответствующий стратегии А2 соединяет величины платежа 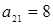 (при
(при 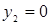 ) и
) и 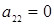 (при
(при 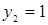 ).
).
Найдем точку М верхней границы получившейся фигуры, которая наиболее приближена к оси абсцисс и сделаем выводы:
- Так как отрезки, соответствующие стратегиям Получателя, пересекаются, выбор заведомо выгодной (доминирующей) стратегии сделать нельзя.
- Точка М находится в точке пересечения отрезков – это говорит о том, что обе стратегии Получателя являются активными.
- Точка М имеет координаты 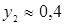 (то есть
(то есть 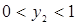 ) и
) и 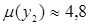 , – это указывает на использование Плательщиком обеих стратегии, что позволяет ему достигать цену игры, меньшую значения
, – это указывает на использование Плательщиком обеих стратегии, что позволяет ему достигать цену игры, меньшую значения 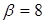 .
.
11. Сформулируем задачу линейного программирования для Получателя (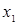 и
и 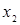 – искомые частотности использования стратегий А1 и А2,
– искомые частотности использования стратегий А1 и А2, 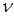 – искомая цена игры,
– искомая цена игры, 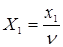 ,
, 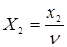 и
и 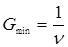 – «вспомогательные»
– «вспомогательные»
ЛП-величины):
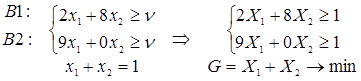
ЛП - задачу можно решить графическим методом. Выполним построения:

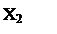
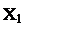

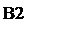
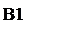
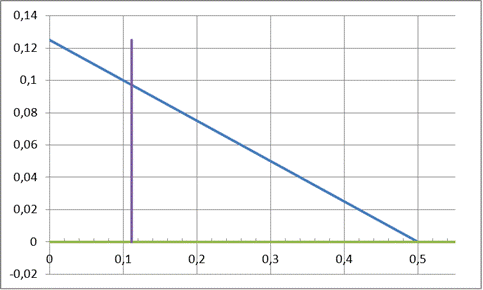
Найдем точку М, удовлетворяющую требованию минимизации целевой функции, и, затем, решение ЛП-задачи: 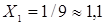 ,
, 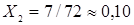 и
и 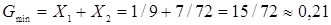 .
.
Решение исходной (игровой) задачи для Получателя находим, используя связи между искомыми и вспомогательными величинами: 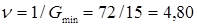 ,
, 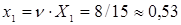 и
и 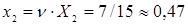 .
.
12. Решение задачи для Плательщика (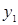 и
и 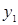 – частотности использования стратегий В1 и В2) найдем, используя следствия из ЛП -теорем двойственности и данных, полученных в предыдущем пункте:
– частотности использования стратегий В1 и В2) найдем, используя следствия из ЛП -теорем двойственности и данных, полученных в предыдущем пункте:
- Так как 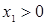 , для активной стратегии А1 записываем точное равенство
, для активной стратегии А1 записываем точное равенство 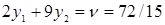 .
.
- Так как 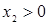 , для активной стратегии А2 записываем точное равенство
, для активной стратегии А2 записываем точное равенство 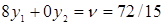
- Дополняем систему требованием 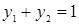 .
.
Эту систему решаем (она оказывается совместной), получая результат: 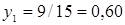 и
и 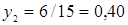 .
.
Ответ:
- Нижняя цена игры 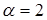 не равна верхней цене игры
не равна верхней цене игры 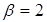 (то есть игра не имеет «седловую точку» и не решается в «смешанных стратегиях»).
(то есть игра не имеет «седловую точку» и не решается в «смешанных стратегиях»).
- Доминируемых рядов в платежной матрице нет.
- Все стратегии игроков являются активными.
- Решение игры: частотности использования Получателем стратегий А1 и А2 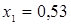 и
и 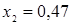 ; частотности использования Плательщиком стратегий В1 и В2
; частотности использования Плательщиком стратегий В1 и В2 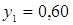 ; и
; и 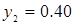 ; цена игры
; цена игры 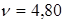 достигается игроками при применении их смешанных стратегий в продолжительной серии игр.
достигается игроками при применении их смешанных стратегий в продолжительной серии игр.
 Пример 9. Для данной платежной матрицы:
Пример 9. Для данной платежной матрицы:
- найти нижнюю и верхнюю цены игры;
- упростить данную платежную матрицу, исключив из неё доминируемые строки и столбцы, соответствующие заведомо невыгодным стратегиям игроков;
- выявить активные стратегии игроков графическим методом;
- найти решение игры: смешанные стратегии игроков и цену игры.
Решение:
1. Введем обозначения стратегий первого игрока (Получателя) и второго игрока (Плательщика):
| В1 | В2 | B3 | B4 | ||
| А1 | |||||
| А2 | |||||
| A3 | |||||
| A4 |
2. В каждой строке выявим наименьшее значение, и из этих результатов – наибольшее:
| В1 | В2 | B3 | B4 | 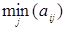
| |
| А1 | |||||
| А2 | |||||
| A3 | |||||
| A4 |
Нижняя цена игры 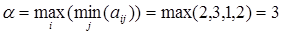 (реализуется при использовании Получателем стратегии А2).
(реализуется при использовании Получателем стратегии А2).
3. В каждом столбце выявим наибольшее значение, и из этих результатов – наименьшее:
| В1 | В2 | B3 | B4 | ||
| А1 | |||||
| А2 | |||||
| A3 | |||||
| A4 | |||||
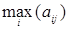
|
Верхняя цена игры 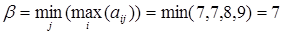 (реализуется при использовании Плательщиком стратегий В1 и B2).
(реализуется при использовании Плательщиком стратегий В1 и B2).
4. По результатам пп. 2,3 сделаем выводы: верхняя и нижняя цены игры не совпадают, значит, игра не имеет решения в чистых стратегиях (следует искать смешанную стратегию), и цена игры лежит в диапазоне 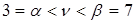 .
.
5. Для выявления доминируемых строк платежной матрицы проведем их поэлементное сравнение:
| В1 | В2 | B3 | B4 | ||
| A1 и А2 | 7>3 | 3<7 | 8>5 | 2<9 | |
| A1 и A3 | 7>1 | 3<5 | 8>4 | 2<8 | |
| A1 и A4 | 7>2 | 3<7 | 8>3 | 2<4 | |
| А2 и A3 | 3>1 | 7>5 | 5>4 | 9>8 | |
| А2 и A4 | 3>2 | 7=7 | 5>3 | 9>4 | |
| А3 и A4 | — | — | — | — |
Вывод: в выделенных строках таблицы знаки неравенств – одинаковые, по сравнению со строкой №2 из платежной матрицы можно исключить строки №№3,4 (стратегия А2 доминирует стратегии А3 и А4). Сравнение доминируемых стратегий между собой не проводилось.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 833; Нарушение авторских прав?; Мы поможем в написании вашей работы!