
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. а) Введем новую переменную интегрирования
|
|
|
|
а) Введем новую переменную интегрирования 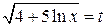 . Тогда
. Тогда 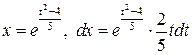 . Найдем пределы интегрирования по переменной
. Найдем пределы интегрирования по переменной  . Из формулы
. Из формулы 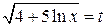 при
при 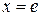 , следует, что
, следует, что  , т. е.
, т. е.  ; при
; при  , следует, что
, следует, что 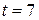 , т.е.
, т.е.  . Тогда по формуле (2.3) получаем
. Тогда по формуле (2.3) получаем
 =
= 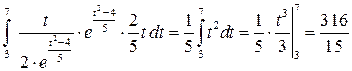 .
.
б) Применим интегрирование по частям:
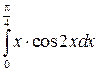 =
= 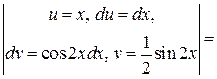
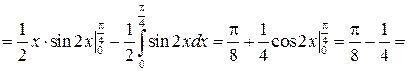
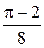 .
.
Площадь криволинейной трапеции, ограниченной графиком функции 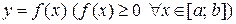 , прямыми
, прямыми 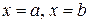 и осью Ох (рис. 1), вычисляется по формуле (2.4).
и осью Ох (рис. 1), вычисляется по формуле (2.4).
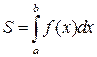 . (2.4)
. (2.4)
Если 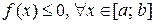 , то
, то  .
.
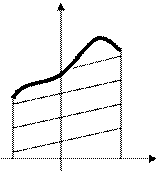
Площадь плоской фигуры, изображенной на рис. 2 (здесь  ), вычисляется по формуле
), вычисляется по формуле
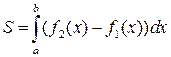 . (2.5)
. (2.5)
 Y
Y
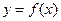
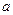
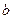 X
X
Рис. 1
 Y
Y

X
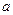
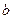
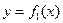
Рис. 2
Пример 2.3. Вычислить площадь фигуры, ограниченной линиями  .
.
Решение. Даны уравнения парабол и прямой. Параболы построим, приведя их уравнения к виду 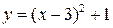 и
и  . Проведя прямую
. Проведя прямую  , определим, площадь какой фигуры требуется вычислить (рис. 3). Ясно, что нижний предел интегрирования в этой формуле равен
, определим, площадь какой фигуры требуется вычислить (рис. 3). Ясно, что нижний предел интегрирования в этой формуле равен  . Верхним пределом интегрирования будет являться абсцисса одной из точек пересечения парабол, которую найдем, решая систему
. Верхним пределом интегрирования будет являться абсцисса одной из точек пересечения парабол, которую найдем, решая систему

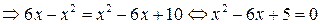 .
.
Корень 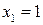 последнего уравнения и есть абсцисса точки пересечения (второй корень
последнего уравнения и есть абсцисса точки пересечения (второй корень  ).
).
Y
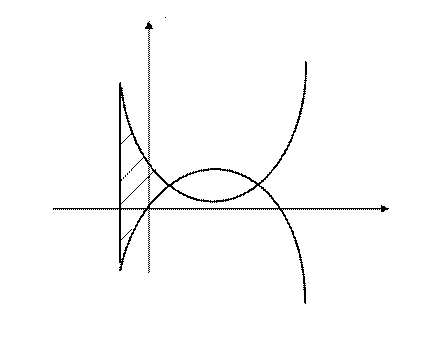
-1 1 3 5 X
Рис. 3
Имеем
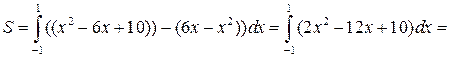
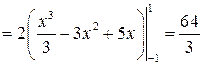 .
.
Объем тела, образованного вращением вокруг оси Ох криволинейной трапеции, которая ограничена графиком функции 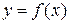 , прямыми
, прямыми 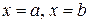 и осью Ох вычисляется по формуле
и осью Ох вычисляется по формуле
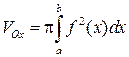 . (2.6)
. (2.6)
Если фигура, ограниченная графиком двух функций 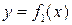 и
и 
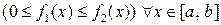 и прямыми
и прямыми 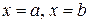 , вращается вокруг оси Ох, то объем тела вращения
, вращается вокруг оси Ох, то объем тела вращения
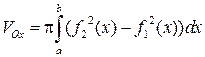 . (2.7)
. (2.7)
Пример 2.4. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 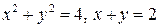 .
.
Решение. Построив окружность 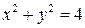 и прямую
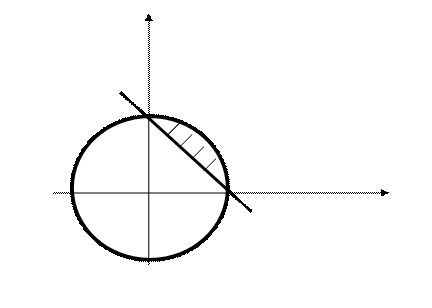
и прямую 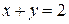 , получим круговой сегмент (рис. 4). При вращении его вокруг оси Ох образуется тело, объем
, получим круговой сегмент (рис. 4). При вращении его вокруг оси Ох образуется тело, объем  которого вычисляется по формуле (2.7), так как этот сегмент ограничен графиком двух функций
которого вычисляется по формуле (2.7), так как этот сегмент ограничен графиком двух функций  и
и  , причем
, причем  . Таким образом,
. Таким образом,
 =
= 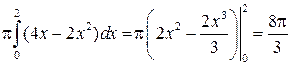 .
.
Y
X
0 2
Рис. 4
Если плоская кривая задана уравнением 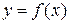 , то длина ее дуги от точки А с абсциссой a до точки В c абсциссой
, то длина ее дуги от точки А с абсциссой a до точки В c абсциссой 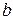 вычисляется по формуле
вычисляется по формуле
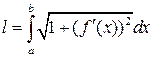 . (2.8)
. (2.8)
Если кривая задана параметрически:
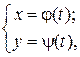
где 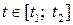 (
(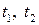 значения параметра
значения параметра  , соответствующие концам рассматриваемой дуги), то длина дуги определяется формулой
, соответствующие концам рассматриваемой дуги), то длина дуги определяется формулой
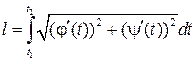 . (2.9)
. (2.9)
Пример 2.5. Вычислить длину дуги кривой, заданной уравнениями:
а) 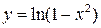 от начала координат до точки
от начала координат до точки  ;
;
б)  при
при  .
.
Решение. а) Находим 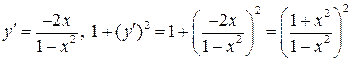 .
.
В соответствии с формулой (2.8) (полагая в ней 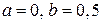 ) имеем:
) имеем:
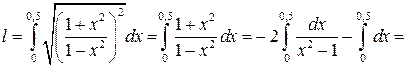
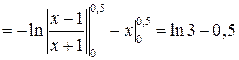 .
.
б) Вычисляем
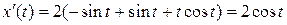 ,
,
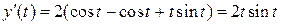 ,
,
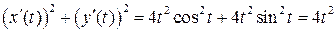 .
.
Согласно формуле (2.9) имеем
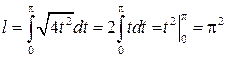 .
.
Задание 2
2.1. Найти площадь фигуры, ограниченной линиями 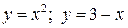 .
.
2.2. Найти длину дуги линии 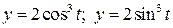 .
.
2.3. Найти площадь фигуры, ограниченной линиями  .
.
2.4. Найти длину дуги линии  , отсеченной прямой
, отсеченной прямой 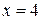 .
.
2.5. Найти объем тела, полученного вращением фигуры Ф:  вокруг оси Ох.
вокруг оси Ох.
2.6. Найти площадь фигуры, образованной линиями  .
.
2.7. Найти длину дуги линии 
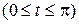 .
.
2.8. Найти объем тела, полученного вращением фигуры Ф: 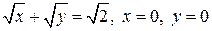 вокруг оси Ох.
вокруг оси Ох.
2.9. Найти площадь фигуры, ограниченной линиями  .
.
2.10. Найти длину дуги линии 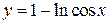
 .
.
2.11. Найти объем тела, полученного вращением фигуры Ф: 
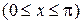 вокруг оси Ох.
вокруг оси Ох.
2.12. Найти площадь фигуры, ограниченной линиями 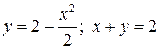 .
.
2.13. Найти длину дуги линии 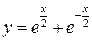
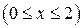 .
.
2.14. Найти объем тела, полученного вращением фигуры Ф: 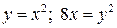 вокруг оси Oy.
вокруг оси Oy.
2.15. Найти площадь фигуры, ограниченной линиями  .
.
2.16. Найти длину дуги линии  от точки А (0; 0) до точки В (4; 8).
от точки А (0; 0) до точки В (4; 8).
2.17. Найти объем тела, полученного вращением фигуры Ф:  вокруг оси Ох.
вокруг оси Ох.
2.18. Найти площадь фигуры, ограниченной линиями 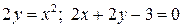 .
.
2.19. Найти длину дуги линии 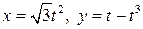 (петля).
(петля).
2.20. Найти объем тела, полученного вращением фигуры Ф:  вокруг оси Oх.
вокруг оси Oх.
2.21. Найти площадь фигуры, ограниченной линиями 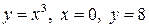 .
.
2.22. Найти длину дуги линии 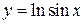
 .
.
2.23. Найти объем тела, полученного вращением фигуры Ф:  вокруг оси Oх.
вокруг оси Oх.
2.24. Найти площадь фигуры, ограниченной линиями 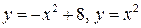 .
.
2.25. Найти длину дуги линии 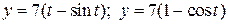 ,
,  .
.
2.26. Найти объем тела, полученного вращением фигуры Ф:  вокруг оси Oх.
вокруг оси Oх.
2.27. Найти площадь фигуры, ограниченной линиями 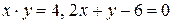 .
.
2.28. Найти длину дуги линии 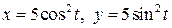 ,
, 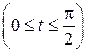 .
.
2.29. Найти объем тела, полученного вращением фигуры Ф: 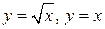 вокруг оси Ох.
вокруг оси Ох.
2.30. Найти площадь фигуры, ограниченной линиями 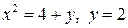 .
.
Тема 3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Пусть функция 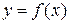 определена на
определена на 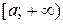 и интегрируема на любом отрезке
и интегрируема на любом отрезке  . Тогда
. Тогда  называется несобственным интегралом от функции
называется несобственным интегралом от функции 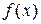 в пределах от
в пределах от 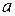 до
до 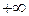 и обозначается
и обозначается 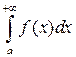 . Таким образом
. Таким образом
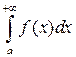 =
= 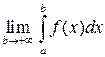 . (3.1)
. (3.1)
Аналогично определяются интегралы
 =
= 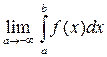 . (3.2)
. (3.2)
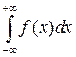 =
= 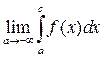 +
+ 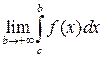 . (3.3)
. (3.3)
(с – любая точка интервала  , чаще
, чаще 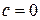 ), где
), где  независимо друг от друга.
независимо друг от друга.
Если приведенные пределы существуют и конечны, то соответствующие интегралы называют сходящимися. В противном случае интегралы называются расходящимися.
Признак сравнения. Если 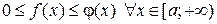 , то из сходимости интеграла
, то из сходимости интеграла 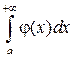 следует сходимость
следует сходимость 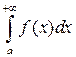 , а из расходимости интеграла
, а из расходимости интеграла 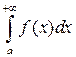 – расходимость интеграла
– расходимость интеграла 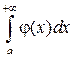 .
.
Пример 3.1. Вычислить несобственный интеграл или установить его расходимость:
а) 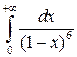 ; б)
; б) 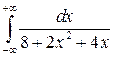 .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 595; Нарушение авторских прав?; Мы поможем в написании вашей работы!