Интегральный признак Коши

Радикальный признак Коши

.

Признак Даламбера

Пусть дан знакоположительный ряд 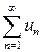и существует конечный или бесконечный предел

.

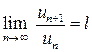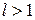Тогда ряд сходится при и расходится при . При 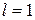ряд может как сходится, так и расходится.

Пример 6.3. Исследовать на сходимость ряд

Применим признак Даламбера:

,

.

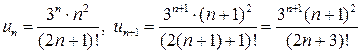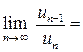
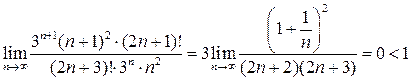По признаку Даламбера ряд сходится.

Пусть дан знакоположительный ряд 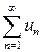и существует конечный или бесконечный предел

.

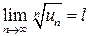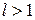Тогда ряд сходится при и расходится при . При 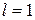ряд может как сходится, так и расходится.

Пример 6.4. Исследовать на сходимость ряд .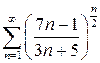

Решение. Применим признак Коши:

.

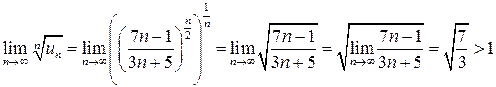По радикальному признаку Коши ряд расходится.

Пусть дан знакоположительный ряд 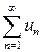. Если функция 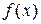непрерывна, монотонно убывает на промежутке 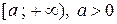, и 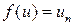для любых 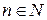, то несобственный интеграл 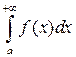и ряд 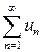сходятся или расходятся одновременно.

Пример 6.5. Исследовать на сходимость ряд .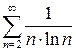

Решение. Применим интегральный признак Коши. Пусть 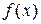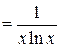–непрерывная, монотонно убывающая на промежутке 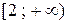функция, .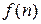

,

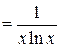
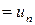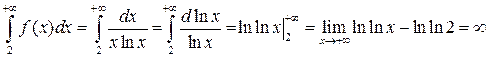т. е. несобственный интеграл расходится. Следовательно, исходный ряд также расходится.

6.3. Абсолютная и условная сходимость знакопеременных рядов

Ряд 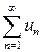называется знакопеременным, если он содержит положительные и отрицательные члены.

Знакопеременный ряд 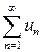называется абсолютно сходящимся, если сходится ряд из модулей .

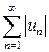Знакопеременный ряд 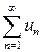называется условно сходящимся, если он сходится, но ряд из модулей 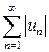расходится.

При исследовании ряда на абсолютную сходимость составляют ряд из модулей и применяют к нему подходящий достаточный признак сходимости знакопеременных рядов или необходимый признак сходимости (см. п. 6.1, 6.2).

Частным случаем знакопеременных рядов являются знакочередующиеся ряды вида

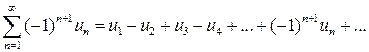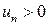, где для .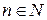

Признак Лейбница (достаточный признак сходимости
знакочередующихся рядов)

Если члены знакочередующегося ряда 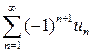удовлетворяют условиям:

1) 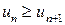для любых ;

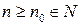2) ,

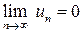то ряд сходится.

Пример 6.6. Исследовать ряды на абсолютную и условную сходимость.

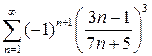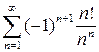а) , б) , в) .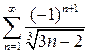

Решение. а) Составим ряд из модулей 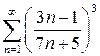. Применим к нему необходимый признак сходимости:

.

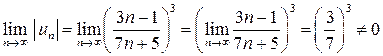Так как 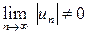, то и 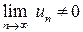, т. е. для исходного ряда нарушен необходимый признак сходимости. Ряд расходится.

б) Составим ряд из модулей 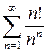. Применим к нему признак Даламбера:

.

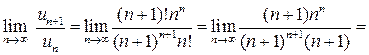
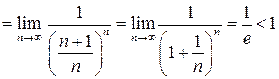Ряд из модулей сходится. Следовательно, исходный ряд сходится абсолютно.

в) Составим ряд из модулей 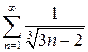. Сравним его с рядом 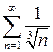по предельному признаку сравнения:

.

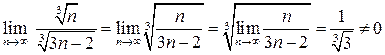Следовательно, ряды ведут себя одинаково. Ряд 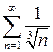является частным случаем обобщенного гармонического ряда при 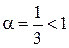, т. е. он расходится. Значит, ряд из модулей также расходится, т. е. абсолютной сходимости у исходного ряда нет.

Исследуем исходный ряд на условную сходимость. Это знакочередующийся ряд. Применим признак Лейбница:

,

.

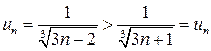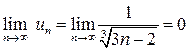Условия признака Лейбница выполнены, значит, ряд сходится.

Итак, исходный ряд сходится условно.

6.4. Степенные ряды

Степенным рядом называются ряды вида

,

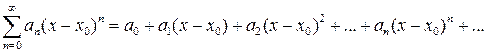где 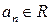– коэффициенты степенного ряда, 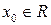– центр ряда.

Подставим в степенной ряд произвольное значение 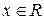. Если полученный при этом числовой ряд сходится, то х называют точкой сходимости степенного ряда, если расходится, то х называют точкой расходимости степенного ряда. Множество всех точек сходимости образует область сходимости D степенного ряда. Отметим, что 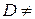¯, так как центр ряда 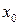всегда содержится в D.

Для каждого степенного ряда существует число 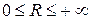, называемое радиусом сходимости, такое, что при 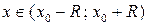этот ряд сходится абсолютно, а при 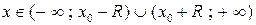расходится. Интервал 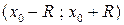называют интервалом сходимости степенного ряда. Вопрос о сходимости ряда на концах интервала, т. е. в точках 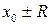решается в каждом конкретном случае отдельных исследованием.

Для определения радиуса сходимости R можно использовать формулы, следующие из признаков Даламбера и Коши:

или ,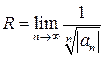

если в правых частях равенств существуют конечные или бесконечные пределы.

Пример 6.7. Найти область сходимости ряда

.

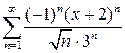Решение. Это степенной ряд с коэффициентами 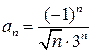, центром ряда 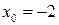. Определим радиус сходимости.

.

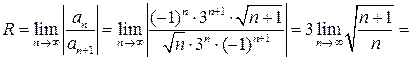
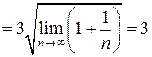Следовательно ряд сходится в интервале 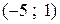и расходится при 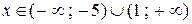. Проведем исследование на концах интервала сходимости.

При 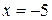получаем обобщенный гармонический ряд 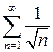, 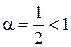и, следовательно, ряд расходится. Точку 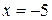не включаем в область сходимости.

При 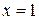получаем знакочередующийся ряд 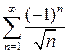, который сходится условно по признаку Лейбница. Точку 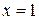включаем в область сходимости.

Область сходимости .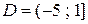

Пример 6.8. Найти область сходимости ряда

.

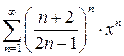Решение. Это степенной ряд с коэффициентами 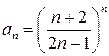, центром ряда 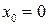. Определим радиус сходимости.

.

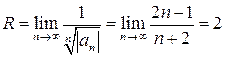Следовательно ряд сходится в интервале 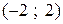и расходится при 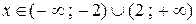. Проведем исследование на концах интервала сходимости.

При 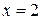получаем числовой ряд 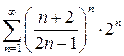, для которого

,

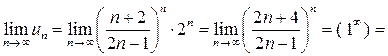
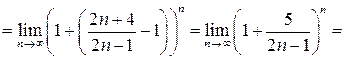
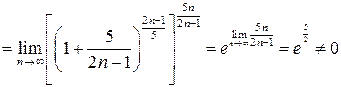т. е. нарушен необходимый признак сходимости.

При 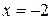получаем знакочередующийся числовой ряд 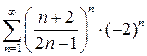, для которого аналогично

.

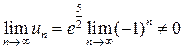Следовательно, точки 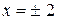не включаем в область сходимости.

Область сходимости .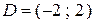

Задание 9

Исследовать ряд на абсолютную и условную сходимость.

9.1. 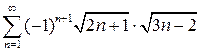. 9.2. 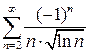. 9.3. .

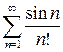9.4. 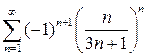. 9.5. 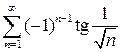. 9.6. .

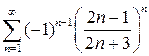9.7. 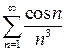. 9.8. 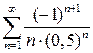. 9.9. .

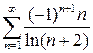9.10. 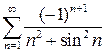. 9.11. 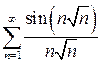. 9.12. .

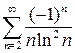9.13. 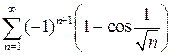. 9.14. 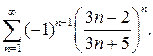9.15. .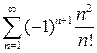

9.16. 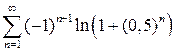. 9.17. 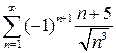. 9.18..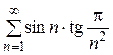

9.19. 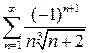. 9.20. 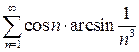. 9.21. .

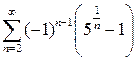9.22. 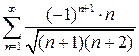. 9.23. 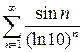. 9.24. .

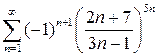9.25. 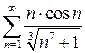. 9.26. 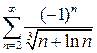. 9.27. .

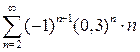9.28. 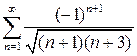. 9.29. 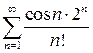. 9.30. .

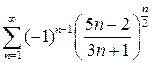Задание 10

Найти область сходимости степенного ряда.

10.1. 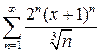. 10.2. 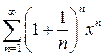. 10.3. .

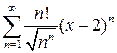10.4. 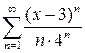. 10.5. 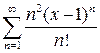. 10.6. .

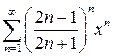10.7. 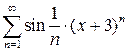. 10.8. 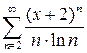. 10.9. .

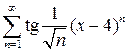10.10. 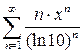. 10.11. 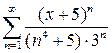. 10.12. .

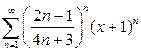10.13. . 10.14. 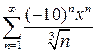. 10.15. .

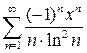10.16. 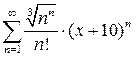. 10.17. 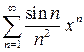. 10.18. .

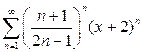10.19. 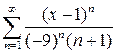. 10.20. 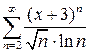. 10.21. .

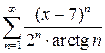10.22. 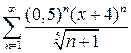. 10.23. 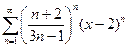. 10.24. .

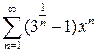10.25. 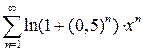. 10.26. 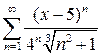. 10.27. .

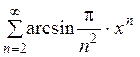10.28. 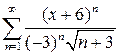. 10.29. 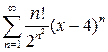. 10.30. .

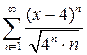ЛИТЕРАТУРА

1. Бугров, Я.С. Элементы линейной алгебры и аналитической геометрии / Я.С. Бугров, С.М. Никольский. – М.: Наука, 1980.

2. Герасимович, А.И. Математический анализ: в 2 ч. / А.И. Герасимович, Н.А. Рысюк. – Минск: Вышэйшая школа, 1989. – Ч. 1.

3. Данко, П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – Минск: Вышэйшая школа, 1986.

4. Сухая, Т.А. Задачи по высшей математике / Т.А. Сухая, В.Ф. Бубнов. – Минск: Вышэйшая школа, 1993.

5. Индивидуальные задания по высшей математике / под ред. А.П. Рябушко. – Минск: Вышэйшая школа, 2008.

6. Руководство к решению задач по высшей математике / под ред. Е.И. Гурского. – Минск: Вышэйшая школа, 1989.

ОГЛАВЛЕНИЕ

Тема 1. НЕОПРЕДЕЛЕНЫЙ ИНТЕГРАЛ......................................................... 3

1.1. Первообразная функция и неопределенный интеграл.

Таблица основных интегралов........................................................................ 3

1.2. Основные методы интегрирования.......................................................... 4

Задание 1............................................................................................................. 6

Тема 2. ОПРЕДЕЛЕНЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ................... 11

Задание 2........................................................................................................... 16

Тема 3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ................................................... 18

Задание 3........................................................................................................... 19

Тема 4. ДВОЙНОЙ ИНТЕГРАЛ...................................................................... 21

Задание 4........................................................................................................... 25

Задание 5........................................................................................................... 27

Тема 5. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ........................................... 30

5.1. Дифференциальные уравнения (ДУ). Основные понятия

и определения................................................................................................ 30

5.2. Дифференциальные уравнения первого порядка.................................. 30

5.3. Дифференциальные уравнения второго порядка,

допускающие понижение порядка................................................................ 35

5.4. Линейные дифференциальные уравнения второго порядка................. 37

Задание 6........................................................................................................... 41

Задание 7........................................................................................................... 42

Задание 8........................................................................................................... 43

Тема 6. РЯДЫ................................................................................................... 45

6.1. Числовые ряды. Необходимый признак сходимости............................ 45

6.2. Достаточные признаки сходимости знакоположительных рядов........ 46

6.3. Абсолютная и условная сходимость знакопеременных рядов............. 49

6.4. Степенные ряды...................................................................................... 51

Задание 9........................................................................................................... 53

Задание 10......................................................................................................... 54

ЛИТЕРАТУРА.................................................................................................. 56

Учебное издание

ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К КОНТРОЛЬНОЙ РАБОТЕ № 2

ПО ВЫСШЕЙ МАТЕМАТИКЕ

для студентов заочного отделения

экономических специальностей

Составители:

КОРЗНИКОВ Александр Дмитриевич

МАТВЕЕВА Людмила Дмитриевна

ШАВЕЛЬ Наталья Александровна

Технический редактор Д.А. Исаев

Подписано в печать 28.03.2011.

Формат 60´84¹/₈. Бумага офсетная.

Отпечатано на ризографе. Гарнитура Таймс.

Усл. печ. л. 6,74. Уч.-изд. л. 2,64. Тираж 200. Заказ 5.

Издатель и полиграфическое исполнение:

Белорусский национальный технический университет.

ЛИ № 02330/0494349 от 16.03.2009.

Проспект Независимости, 65. 220013, Минск.

Дата добавления: 2014-12-27