Экстремумы функции нескольких переменных

Говорят, что функция 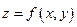имеет максимум (минимум) в точке 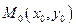, если для всех точек из 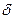- окрестности точки 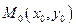выполняется неравенство 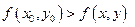(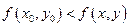). Максимум или минимум функции называется её экстремумом.

Если функция 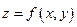имеет частные производные и точка 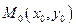- точка экстремума функции 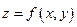, то частные производные функции 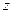в этой точке равны нулю:

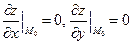(13)

(необходимый признак существования экстремума функции двух переменных).

Точки, в которых 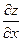и 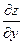равны нулю или не существуют, называются критическими. Таким образом, точки экстремума функции следует искать среди её критических точек.

Следующая теорема дает достаточный признак существования экстремума функции двух переменных:

1) если выполнено условие:

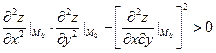, (14)

то в точке 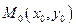функция 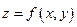имеет экстремум, причем в случае 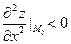точка 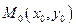- точка максимума, а в случае 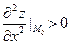точка 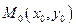- точка минимума;

2) если выполнено условие:

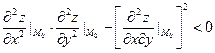, (15)

то у функции 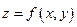нет экстремума в точке ;

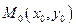3) если выполнено условие:

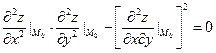, (16)

то вопрос о наличии у функции 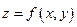в точке 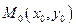экстремума остается открытым – требуются дополнительные исследования.

Функция 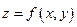, непрерывная в замкнутой области 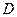и дифференцируемая внутри неё, достигает своего наибольшего (наименьшего) значения либо внутри области 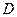, либо на её границе.

Нахождение наибольшего и наименьшего значений данной функции рекомендуется проводить по следующей схеме:

1. Найти критические точки, лежащие внутри области 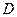, и вычислить значения функции в этих точках.

2. Найти наибольшее и наименьшее значения функции на каждой линии, ограничивающей область. Это сводится к нахождению наибольшего и наименьшего значений функции одной переменной.

3. После этого среди всех полученных значений найти наибольшее наименьшее. Эти значения и будут соответственно наибольшим и наименьшим значениями функции в замкнутой области .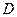

Задание. Найти наибольшее и наименьшее значения функции в замкнутой области 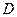, ограниченной прямой 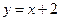и параболой .

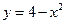Решение. 1. Сделаем чертеж области :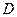

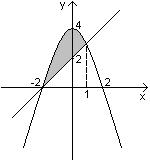
2. Найдем критические точки данной функции 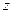, лежащие внутри области 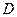. Для этого найдем частные производные функции 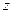и приравняем их к нулю:

,

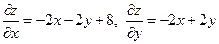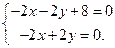
Решением системы является значения:

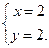
Точка 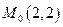не принадлежит замкнутой области 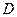. Следовательно, наибольшее и наименьшее значения данная функция 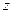может принимать только на границе области .

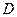3. Исследуем функцию 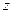на границе области .

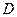1) На отрезке прямой 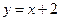имеем функцию

,

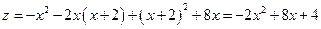которая представляет собой функцию одной переменной 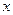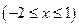. Её наибольшее и наименьшее значения следует искать среди её значений в критических точках и на концах отрезка 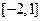. Найдём производную функции 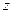и приравняем её к нулю:

.

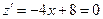Решая полученное уравнение, находим:

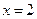
- критическая точка, но она не принадлежит отрезку 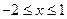. Следовательно, наибольшее и наименьшее значения функция 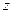принимает на концах отрезка :

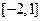2) На дуге параболы 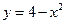имеем функцию

,

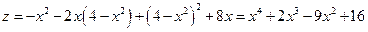которая представляет собой функцию одной переменной 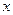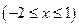. Найдем производную функции 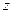и приравняем к нулю:

.

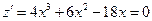Решая полученное уравнение, находим его корни:

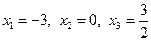
- критические точки, из которых только значение 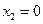принадлежит отрезку 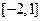. Следовательно, наибольшее и наименьшее значения функция 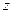принимает либо в точке 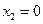, либо на концах отрезка :

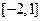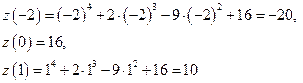
Сравнивая все вычисленные значения функции 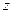, находим наибольшее и наименьшее значения данной функции в замкнутой области 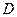: - наибольшее значение (в точке 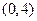); 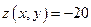- наименьшее значение (в точке ).

Дата добавления: 2014-12-27