Проверка эмпирического распределения на его соответствие нормальному распределению 2 страница

Порядок расчета эмпирического значения критерия следующий:

1. Проранжировать все измерения, объединив результаты выборок. Наименьшему значению из всех присваивается ранг 1, наибольшему - N = n₁+n₂+.... Если два или большее количество значений равны, то для них рассчитывается средний ранг, как это делали, рассматривая критерий Манна-Уитни.

2. Подсчитать сумму рангов отдельно для первой (SR₁), второй (SR₂) третьей (SR₃) и других выборок. Проверить, совпадает ли общая сумма рангов с расчетной по формуле SR₁+SR₂+SR₃+ +...=N(N+1)/2, где N= n₁+n₂+n₃+... - общее число ранжируемых значений.

3. Рассчитать эмпирические значения критерия Вилкоксона для множественных значений. За эмпирические значения принимаются разности сумм рангов между всеми выборками попарно. Результаты удобно представить в виде матрицы. В заголовках строк и столбцов такой матрицы находятся названия выборок и суммы рангов для каждой из них, а на пересечении строк и столбцов матрицы указываются абсолютные значения разностей, показывающие, насколько отличаются суммы рангов соответствующих выборок. Матрица получается симметричной относительно главной диагонали, в ячейки главной диагонали нули можно не записывать.

4. Сравнить эмпирические значения критерия с критическими, приведенными в соответствующей таблице (Таблица 7 Приложения). Если эмпирическое значение больше ли равно критическому, то принимается альтернативная гипотеза, если меньше - то нулевая.

Задача: В одной из школ Ленинградской области ученики 10 и 11 класса выполнили задания ШТУР (Школьный тест умственного развития). Различаются ли ученики - юноши и девушки из 10 и 11 классов по уровню общей осведомленности?

Н0: уровень общей осведомленности у юношей и девушек из 10 и 11 классов значимо не различается.

Н1: показатели уровня общей осведомленности у юношей и девушек из 10 и 11 классов различаются значимо.

Таблица 12

Сравнение уровня общей осведомленности юношей и девушек 10 и 11 классов одной из школ Ленинградской области (По критерию Вилкоксона для множественных сравнений)
Юноши, 11 класс*	Девушки, 11 класс*	Юноши, 10 класс	Девушки, 10 класс*
Общая осведомленность	Ранг	Общая осведомленность	Ранг	Общая осведомленность	Ранг	Общая осведомленность	Ранг
	49		42,5		55		1,5
	33,5		23,5		42,5		4,5
	13		23,5		37,5		6,5
	42,5		33,5		42,5		9
	42,5		55		42,5		13
	33,5		19,5		55		13
	19,5		55		37,5		13
	59,5		55		19,5		16,5
	16,5		42,5		28		23,5
	59,5		33,5		13		28
	28		9		9		28
	55		55		4,5		28
	42,5		23,5		19,5		33,5
	49		23,5		3		49
	49		6,5		1,5		49
Ме=17 q=2		Ме=15 q=3		Ме=14 q=4		Ме=11 q=2.5
Суммы рангов по группам:	592,5		501		410,5		316

* - для данных групп использованы случайные выборки по 15 человек из имеющихся результатов ШТУР.

Таблица 13

Эмпирические значения Т (Тэмп=SRa-SRb)
	Юноши, 11 класс	Девушки, 11 класс	Юноши, 10 класс	Девушки, 10 класс
Юноши, 11 класс		91,5	182	276,5
Девушки, 11 класс	91,5	0	90,5	185
Юноши, 10 класс	182	90,5	0	94,5
Девушки, 10 класс	276,5	185	94,5

Tкр.=246 (a=0.05)

Т эмп > Tкр только в одном случае (девушки 10 класса и юноши 11 класса).

Ответ: различия в уровне общей осведомленности значимы между девушками 10 класса и юношами 11 класса (a=0.05).

7.4 Сравнение уровня признака в зависимых выборках

При сопоставлении уровня результатов в двух зависимых выборках, когда измерения производятся на одних и тех же испытуемых в различных условиях X и Y, следует учитывать взаимозависимость результатов у каждого отдельного испытуемого.

Формула t-критерия Стьюдента при решении задачи такого рода имеет вид

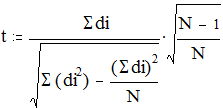
где di = x_i - y_i, т.е. разности значений признака для каждого испытуемого. Следует различать S (di²) - сумму квадратов di - и (S di) ² - квадрат суммы di.

Количество степеней свободы определяется по формуле

n = N-1

Корректное применение t-критерия предполагает, что распределение признака относится к нормальному типу. Альтернативная гипотеза принимается, если t _эмп³ t _кр. Задача сравнения результатов двух зависимых выборок предполагает направленное изменение результатов в ту или иную сторону, поэтому критические значения t _кр берутся из колонки для одностороннего критерия.

В программе Microsoft Excel расчет эмпирического значения критерия Стьюдента для зависимых выборок выполняется с использованием встроенного «Парного двухвыборочного t-теста для средних». Чтобы воспользоваться встроенной функцией Microsoft Excel надо войти в раздел «Анализ данных» из меню «Сервис», где и выбрать «Парный двухвыборочный t-тестдля средних». На экране высвечивается меню «Парного двухвыборочного t-теста для средних», в котором задаются интервалы обеих переменных, вероятность ошибки первого рода Альфа и выходной интервал (номер левой верхней ячейки выходного интервала). Гипотетическая средняя разность равна нулю по умолчанию. Выходные данные включают средние арифметические значения переменных в выборках, значения дисперсии, количество наблюдений в выборках, коэффициент линейной корреляции Пирсона, число степеней свободы, эмпирическое значение t-критерия и критические значения для одностороннего и двустороннего критериев.

Задача: Учащиеся старших классов выполняли тест ADOR в десятом, а затем через год в одиннадцатом классе. Увеличился ли за это время показатель враждебности к матери у девушек-учениц данной школы?

Н0: уровень враждебности к матери у девушек в 11 классе значимо не выше такового в 10 классе.

Н1: показатели уровня враждебности к матери у девушек в 11 классе выше уровня враждебности, который был за год до этого - в 10 классе.

Таблица 14

Оценка значимости изменения показателя враждебности к матери по тесту ADOR для учениц одной из школ Ленинградской области (по t-критерию Стьюдента)
Результат по тесту ADOR
в 11классе	в 10 классе	d	d^2
		-6
		-2
		-6
		-4
		-6
		-2
		-1
		Sdi =114	S(di^2) =1354
Мх = 9.50 s = 4.937	Мх = 6.15 s = 3.421	(Sdi)^2/34= 382,2
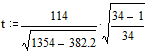
	=3,603	t кр.=2.44 (a=0.01)
tэмп.>tкр.Þ принимается альтернативная гипотеза. Ответ: враждебность девушек в 11 классе по отношению к матери (по тесту ADOR) значимо выше, чем она была у них за год до этого (р=0.01).

Если измерения проводились на двух зависимых выборках, но распределение признака хотя бы в одной из них оказалось отличным от нормального, либо недостаточным является объем выборок, то для оценки значимости изменений в этом случае используется непараметрический Т-критерий Вилкоксона для попарных сравнений. Т-критерий Вилкоксона применяется для признаков, измеренных в шкалах рангов, интервалов или отношений в двух различных условиях на одной и той же группе испытуемых. Критерий используется при минимальном количестве испытуемых 5 человек, а максимальное количество - 50 испытуемых (это ограничение связано с тем, что для большего числа испытуемых критические значения критерия не рассчитаны).

Вычисления производятся в следующей последовательности:

1. Находится разность результатов для каждого испытуемого: из результата при условии 2 вычитается результат при условии 1.

2. Полученные разности ранжируются от наименьшего к наибольшему по абсолютной величине. Нулевые разности не учитываются.

3. Отдельно записываются ранги положительных и отрицательных разностей и суммируются отдельно. Правильность подсчета суммы рангов проверяется так же, как в критерии Манна-Уитни.

4. В качестве эмпирического значения принимается наименьшая сумма рангов.

5. Эмпирическое значение Т-критерия сравнивается с табличными значениями критических значений для a=0.05 и a=0.01 (Таблица 8 Приложения) и числа испытуемых в исходной выборке. Нулевая гипотеза отклоняется, если Т_эмп £ Т_крит.

Аналогично приведенным выше задачам, если нас интересует только сам факт наличия изменений в выборке, то используются критические значения для двустороннего критерия, а если нам важна направленность изменений (при использовании Т-критерия Вилкоксона это случается чаще), то берутся критические значения для одностороннего критерия.

Задача: Учащиеся старших классов (юноши) выполняли тест ADOR в десятом, а затем через год в одиннадцатом классе. Увеличился ли за это время показатель враждебности к отцу у юношей - учеников данной школы?

Н₀: уровень враждебности к отцу у юношей в 11 классе не выше такового в 10 классе.

Н₁: показатели уровня враждебности к отцу у юношей в 11 классе значимо выше уровня враждебности, который был за год до этого - в 10 классе.

Таблица 15

Оценка значимости изменения показателя враждебности к отцу по тесту ADOR для учеников одной из школ Ленинградской области
11 класс	10 класс	Разность	Абс.значение разности	Ранговый номер
		-8		9,5
		-1		1,5
		-6
				1,5
				9,5
Me= 7 q=3.75	Me=5 q=2.75
Сумма
T(+) =
T(-) =

Т эмп.=18. Ткр.=19 (при a=0.01)

Т эмп.< Ткр. (при a=0.01) Þ принимается альтернативная гипотеза.

Ответ: показатель враждебности к отцу у учеников 11 класса значимо выше, чем он был за год до этого (р=0.01).

L-критерий Пейджа по своему назначению схож с Т-критерием Вилкоксона, с той разницей, что он применяется для сопоставления трех и более показателей, измеренных на одной и той же выборке испытуемых. При этом он не только констатирует наличие изменений, но и указывает их направление. Критерий позволяет проверить наши предположения об определенной возрастной или ситуативной динамике. Таблицы критических значений критерия рассчитаны лишь для небольших выборок (от 2 до 12 испытуемых) и ограниченное количество сопоставляемых замеров (до 6).

Порядок действий при использовании L-критерия Пейджа следующий:

1. Проранжировать индивидуальные значения, полученные в первом, втором, третьем и т.д. замерах для каждого из испытуемых. Самому низкому значению присвоить ранг 1, самому высокому - наивысший, согласно числу замеров.

2. Просуммировать ранги по условиям, при которых выполнялись замеры. Проверить совпадение общей суммы рангов с расчетной по формуле SR=nc(c+1)/2, где n - число испытуемых, с - число замеров.

3. Расположить условия в таблице в порядке возрастания ранговых сумм.

4. Определить значение L по формуле

L=S(T_j^.j),

где T_j- сумма рангов по данному условию, а j - порядковый номер, приписанный данному условию в упорядоченной последовательности условий.

5. По таблицам критических значений (Таблица 9 Приложения) определить критические значения L для данного количества испытуемых N и для данного количества условий с. Если L равен критическому значению или превышает его, то тенденция достоверна.

Задача: Изменяется ли уровень тревожности испытуемых в течение дня?

Таблица 16

№	Утром	Днем	Вечером

Н₀: уровень тревожности в течение дня значимо не изменяется.

Н₁: уровень тревожности в течение дня значимо повышается.

Таблица 17.

№	Утром	Ранг	Днем	Ранг	Вечером	Ранг
		2.5				2.5
		1.5		1.5
Сумма рангов			12.5		19.5

Результаты ранжирования по строкам и суммы рангов для каждого из условий приведены в таблице. Проверка по формуле SR = n c(c+1)/2=42 подтверждает правильность ранжирования. Колонки расположены в порядке возрастания ранговых сумм, поэтому колонка «утро» получает номер 1, колонка «день» номер 2 и «вечер» - номер 3. Теперь можно рассчитать эмпирическое значение L-критерия: L_эмп=10^х1+12.5^х2+19.5^х3 = 93.5. Эмпирическое значение критерия L_эмп больше критического L_кр=93 для уровня доверительной вероятности 95%, поэтому можно принять альтернативную гипотезу.

Ответ: тенденция увеличения уровня тревожности в течение дня является достоверной (a=0.05).

7.5 Оценка сходства-различия распределений признаков

Для установления сходства - различия между эмпирическим и теоретическим распределениями (равномерным, нормальным или каким-то иным) используется c²- критерий Пирсона

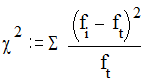
где f_i - эмпирическая частота для интервала квантования, f_t - теоретическая (ожидаемая) частота для того же интервала. Сравнение эмпирического распределения с нормальным уже рассмотрено ранее. При сравнении эмпирического распределения с равномерным теоретическая (ожидаемая) частота интервала квантования находится по простой формуле:

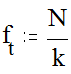
Количество степеней свободы для сравнения эмпирического распределения с равномерным определяется по формуле

n= k-1

где k - число групп или интервалов квантования.

Задача: определить, равномерно ли распределяется число полученных учениками неудовлетворительных оценок по месяцам учебного года.

Подсчитав по классному журналу «двойки» учеников, получили следующие результаты:

Таблица 18.

Месяц	Сен	Окт	Нояб	Дек	Янв	Фев	Март	Апр	Май
Кол-во «двоек»

Общее число «двоек» N=135. Если бы все они были распределены равномерно по 9 месяцам учебного года (k=9), то каждый месяц ученики получали бы 135/9=15 двоек. Это число 15 является теоретической частотой f_t для расчета величины c². Значения эмпирической частоты f_i даны в условии задачи (таблица).

Н₀: Распределение неудовлетворительных оценок по месяцам учебного года не отличается значимо от равномерного.

Н₁: Распределение неудовлетворительных оценок по месяцам учебного года значимо отличается от равномерного.

Рассчитываем критерий c² Пирсона:

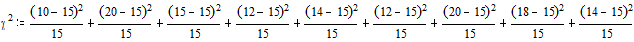
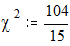
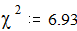
Критическое значение критерия c² определяется по таблицам (Таблица 3 Приложения), в нашем случае при n=9-1=8 и a=0.05 оно будет равным 15.51, при a=0.10

c²_кр. =13.36, и при a=0.20 c²_кр. =11.03.

Ответ: мы должны принять нулевую гипотезу и признать, что распределение двоек по месяцам статистически значимо не отличается от равномерного (a=0.20).

Непараметрический критерий l Колмогорова-Смирнова можно использовать для сравнения двух любых распределений, между собой. Критерий основан на сравнении накопленных частот в двух распределениях, упорядоченных по тому или иному принципу. Порядок применения критерия для сравнения двух эмпирических распределений следующий:

1. Упорядочить распределения по одному и тому же основанию (принципу). Например, рассматривая темперамент учащихся двух классов, мы в первый интервал заносим данные меланхоликов, затем во второй интервал - флегматиков, потом сангвиников и, наконец, холериков как в первой, так и во второй выборках.

2. Для каждого интервала распределения рассчитать относительную частоту

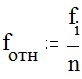
где f_i - абсолютная частота интервала, а n - объем соответствующей выборки.

3. Рассчитать накопленные частоты, сложив f_отн каждого интервала с относительными частотами всех предшествующих интервалов. Накопленная частота последнего интервала равна 1.00.

4. Рассчитать разность накопленных частот соответствующих интервалов двух распределений. Наибольшая по абсолютной величине (то есть без учета знака) из рассчитанных разностей используется для расчета эмпирического значения l

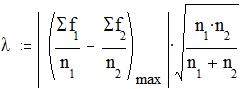
где (Sf₁/n₁ - Sf₂/n₂)_max - наибольшая разность накопленных частот, а n₁ и n₂ - объем выборок.

5. Сформулировать нулевую и альтернативную гипотезы:

Н₀: Распределение 1 значимо не отличается от распределения 2.

Н₁: Распределение 1 значимо отличается от распределения 2.

6. Сравнить эмпирическое значение с критическим. Критические значения составляют:

Таблица 19.

Доверительная вероятность	0.80	0.90	0.95	0.99	0.999
Критическое значение l	1.07	1.22	1.36	1.63	1.95

Если эмпирическое значение больше критического, то принимается альтернативная гипотеза, если меньше, то нулевая.

Задача: Сопоставить профили распределения результатов ШТУР учениц 11 класса, показавших наилучший и наихудший результаты:

Таблица 20

Разделы ШТУР	Баллы «лучшей» ученицы	Относи-тельная частота	Накопленная частота	Баллы «худшей» ученицы	Относи-тельная частота	Накопленная частота	Разность накопленных частот
общая осведомленность		0,1626	0,163		0,2727	0,273	0,110
частная осведомленность		0,1626	0,325		0,1636	0,436	0,111
способности классификации		0,1789	0,504		0,1091	0,545	0,041
способности поиска аналогии		0,1626	0,666		0,1455	0,691	0,025
способности обобщения		0,2358	0,902		0,2909	0,982	0,080
способности выполнения счетных операций		0,0976	1,000		0,0182	1,000	0,000
Сумма

Н₀: Профили распределения результатов ШТУР лучшей и худшей учениц значимо не отличаются друг от друга.

Дата добавления: 2014-12-27