Меры связи для явлений, измеренных в разных шкалах

Для изучения связей между явлениями, одно из которых измерено в шкале интервалов или отношений, а второе - в дихотомической номинативной шкале, используется точечно-бисериальный коэффициент корреляции r_pb.

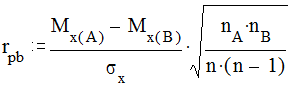
где М_х(А) - среднее значение х для объектов, имеющих «А» по шкале наименований, М_х(В) - среднее х для объектов, имеющих «В» по шкале наименований, s_х - среднеквадратическое отклонение всех объектов (то есть объединенной выборки!), n_А - число объектов, имеющих «А» в шкале наименований, n_В - число объектов, имеющих «В» в шкале наименований, N- общее количество наблюдений. Точечно-бисериальный коэффициент корреляции может быть использован вместо t-критерия Стьюдента для выявления значимости различий в уровне признака в двух независимых выборках.

Точечно-бисериальный коэффициент корреляции варьирует от -1 до 1. Если коэффициент близок к нулю - связь отсутствует, если по абсолютной величине приближается к 1, связь есть. Знак значения не имеет. Проверить статистическую значимость точечно-бисериального коэффициента корреляции можно, воспользовавшись таблицами критических значений коэффициента линейной корреляции Пирсона (Таблица 11 Приложения) (коэффициент корреляции следует признать статистически значимым, если он превышает табличное критическое значение или равен ему) или с помощью критерия Стьюдента для мер связи по формуле:

где N - количество испытуемых, а r - коэффициент корреляции. Число степеней свободы n = N-2 (связь признается значимой, если t_эмп. больше или равно t_крит.). Пример решения задачи на расчет точечно-бисериального коэффициента корреляции приведен в таблице 27.

Если явления измерены у объектов одно в ранговой, а другое в номинативной шкалах, то есть каждый испытуемый отнесен к одному из двух классов шкалы наименований, и ему присвоен какой-то ранг по другому качеству, то используется рангово-бисериальный коэффициент корреляции r_rb:

где М_RA - среднее значение рангов по х для объектов, имеющих «А» по шкале наименований (ранги рассчитываются для объединенной выборки, затем расписываются на относящиеся к А и к В), М_RВ - среднее значение рангов для объектов, имеющих «В» по шкале наименований. Рангово-бисериальный коэффициент корреляции может быть использован вместо критерия Манна-Уитни для выявления значимости различий в уровне признака в двух независимых выборках.

Задача: Зависит ли способность ученика к обобщению (по ШТУР) от года обучения в школе (сопоставляются результаты учеников 10 и 11 классов)?

Таблица 27

Оценка зависимости между способностью обобщения и годом обучения в школе у учениц одной из школ Ленинградской области(по точечно-бисериальному коэффициенту корреляции)
11 класс	10 класс
Среднее 21,40	15,76
Общее среднее 18,97
Общее стандартное отклонение 6,782
Общая дисперсия выборки 46,00
	=0.414

r_Pb > r_кр (r_кр=0,283 при a=0.01)

Ответ: между способностью к обобщению по ШТУР и годом обучения в школе есть высокая значимая связь (a=0.01).

Аналогично точечно-бисериальному коэффициенту корреляции, рангово-бисериальный коэффициент изменяется от -1 до 1, знак значения не имеет. Проверка значимости проводится с помощью таблиц критических значений для коэффициента корреляции Пирсона (Таблица 11 Приложения), либо с применением t-критерия Стьюдента для мер связи.

Задача: Зависит ли способность ученика выполнять счетные операции (по ШТУР) от года обучения в школе: сопоставить результаты учеников 10 и 11

классов.

Таблица 28.

Оценка зависимости выполнения счетных операций по результатам ШТУР от года обучения у юношей одной из школ Ленинградской области(по рангово-бисериальному коэффициенту корреляции)
Результат ШТУР	Ранг	Результат ШТУР	Ранг
	16,5
	16,5		16,5
	16,5		16,5
	16,5		16,5
	16,5		16,5
	16,5
			28,5
			28,5
	28,5
	28,5
	34,5
	34,5
Сумма рангов
Средний ранг	19,55		13,80

r_rb=(2/35)^.(19.55-13.80)=0.329.

r_кр=0,334 (a=0.05) > r_rb > r_кр=0,284 (a=0.10) Þ

Ответ: между выполнением счетных операций по ШТУР и годом обучения есть тенденция достоверной связи (р=0.10).

8.2.3 Меры связи для явлений, измеренных

Дата добавления: 2014-12-27