Проверка эмпирического распределения на его соответствие нормальному распределению 3 страница

Н₁: Профили распределения результатов ШТУР лучшей и худшей учениц различаются значимо.

Максимальное значение разности накопленных частот 0,111.

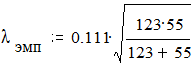
l_эмп. = 0,111×6,165 = 0.684. l_эмп.< l_кр.(при доверительной вероятности 0.95), следовательно, принимается нулевая гипотеза.

Ответ: Профили распределения результатов ШТУР «лучшей» и «худшей» учениц не различаются значимо.

8. ИЗУЧЕНИЕ ВЗАИМОСВЯЗИ ПСИХОЛОГИЧЕСКИХ ЯВЛЕНИЙ

8.1 Меры связи явлений, измеренных в номинативных шкалах

Коэффициент четырехклеточной сопряженности. Когда объекты классифицированы по двум или нескольким свойствам, то результат такой классификации можно представить в виде таблиц, в которых строки будут иметь заголовки одного свойства, а столбцы - другого, а сочетания всех свойств будут рассматриваться попарно. Такие таблицы называются таблицами сопряженности. В заголовки столбцов выносятся свойства Х₁, Х₂ и т.д. до X_i, в заголовки строк У₁, У₂ и т.д. до Y_j. В клетки таблицы заносим частоту - то есть количество случаев сочетания Х₁ и У₁ (записывается Х₁ и У₁), Х₁У₂, Х₁У₃ и т.д. до Х₁У_j в первой строке, Х₂У₁, Х₂У₂..... X₂Y_j во второй строке, и так по всей таблице вплоть до нижней правой клетки, где будет X_iУ_j.

Силу связи между двумя явлениями, измеренными в дихотомической номинативной шкале, оценивают с помощью коэффициента четырехклеточной сопряженности Пирсона j:

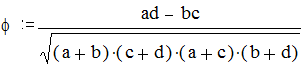
В данной формуле a, b, c, d - это количество случаев в каждой ячейке таблицы: a, b - в верхней строке справа налево, c и d - в нижней строке. Коэффициент j может изменяться от -1 до 1. Если он равен нулю, то связь отсутствует, если близок к нулю - связь слабая, а если приближается к 1 (или -1) или равен ей, то связь сильная.

С помощью коэффициента 4-х-клеточной сопряженности Пирсона можно непосредственно сравнивать между собой силу связи по двум и более таблицам сопряженности - коэффициент четырехклеточной сопряженности указывает, что в таблице А связь сильнее, чем в таблице Б. Статистически же точный ответ, значимо ли отличается коэффициент j от нуля, то есть значима ли связь между явлениями, можно получить с помощью критерия c² Пирсона.

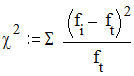
где f_i - эмпирическая частота, а f_t - теоретическая частота для ячейки таблицы. Эмпирическая частота - это те значения абсолютной частоты, которые приведены в таблице сопряженности. Теоретическая частота - это та частота, которая значилась бы в данной ячейке при равномерном распределении характеристик. Теоретическая частота рассчитывается согласно правилу вероятности произведения случайных независимых событий по формуле:

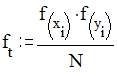
где f(x_i)- сумма по соответствующей строке, f(y_j) - сумма по соответствующему столбцу, а N- общее число испытуемых.

Знак суммы в формуле критерия Пирсона говорит о том, что сложение проводится для всех клеток таблицы.

Число степеней свободы n определяется по формуле

n = (n-1)(m-1)

где n - число строк в таблице, а m - число столбцов, т.е. для четырехклеточных таблиц n=1. Если эмпирическое значение критерия c² оказывается больше (или равно) критического при заданном уровне доверительной вероятности, то отличие коэффициента j от нуля признается статистически значимым.

Для четырехклеточных таблиц с числом испытуемых меньше 30 рекомендуется использовать формулу с учетом поправки Йетса на непрерывность:

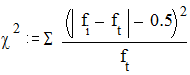
Задача: Есть ли связь между результатами сдачи зачета, посещением лекций и местом проживания? Какая из этих связей более сильная?

А. Связь «посещаемость - сдача зачета»:

(здесь и ниже: цифра слева вверху ячейки - эмпирическая частота, справа внизу - теоретическая частота)

Таблица 21

	У1 - посещал лекции	У2 - не посещал лекции	Сумма по строке
Х1 - сдал зачет с 1-го раза	12.87	8.13
Х2-не сдал зачет с 1-го раза	6.13	3.87
Сумма по столбцу			Всего 31
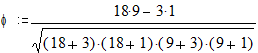
	= 0.727

Статистическую значимость отличия коэффициента j от нуля проверим по критерию c² Пирсона:

c²_эмп= (18-12.87)² ₊ (3-8.13)² ₊ (1-6.13)² ₊ (9-3.87) ² _{= 16.375}

12.87 8.13 6.13 3.87

c²_кр=6.635 (a=0.01)

c²_эмп > c²_крÞ связь «посещаемость - сдача зачета» статистически значима (0.01).

Б. Связь «место проживания - сдача зачета»:

Таблица 22.

	У1 - живет дома	У2- живет в общежитии	Сумма по строке
Х1 - сдал зачет с 1-го раза	10.29	7.71
Х2-не сдал зачет с 1-го раза	5.71	4.29
Сумма по столбцу			Всего 28
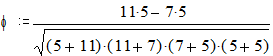
	=0.107

Статистическая значимость связи «место проживания - сдача зачета» проверяется по критерию c² с учетом поправки Йетса, так как число испытуемых меньше 30:

c²_эмп= (11-10.29-0.5)² ₊ (|7-7.71|-0.5)² ₊ (|5-5.71|-0.5)² + (5-4.29-0.5)² _{= 0.028}

10.29 7.71 5.71 4.29

c²_кр=3.841 (a=0.05)

c²_эмп < c²_крÞ связь «место проживания - сдача зачета» статистически незначима (0.05).

Ответ: Коэффициент четырехклеточной сопряженности для зависимости «посещаемость - сдача зачета» выше, чем для зависимости «место проживания - сдача зачета», следовательно, в первой зависимости связь сильнее.

Если таблицы описывают свойства, измеренные в недихотомической шкале наименований, то они называются таблицами многоклеточной сопряженности.

Для анализа многоклеточных таблиц используются коэффициенты многоклеточной сопряженности К_ч - коэффициент Чупрова и - коэффициент Пирсона. Коэффициенты рассчитываются по формулам:

С - коэффициент многоклеточной сопряженности Пирсона:

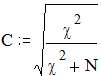
где N - общее количество испытуемых, c²- критерий Пирсона.

К_ч - коэффициент Чупрова:

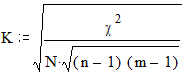
где n-число строк, m - число столбцов, N - общее количество испытуемых.

Непосредственно по коэффициентам многоклеточной сопряженности К и С, как и в случае с четырехклеточными таблицами, можно сравнивать силу связи между изучаемыми характеристиками в разных таблицах. Статистическая значимость связи и отличия от нуля коэффициентов Чупрова и Пирсона оценивается по критерию c² Пирсона аналогично четырехклеточным таблицам (с учетом поправки Йетса при количестве измерений менее 30).

Задача: При исследовании связи между удовлетворенностью профессиональной деятельностью, уровнем образования и социальным положением испытуемых получены результаты, приведенные в таблицах. Какие выводы можно сделать о силе связи между этими характеристиками?

Таблица 23.

Удовлетворенность профессиональной деятельностью	Уровень образования	Суммы по строкам
Высшее	Ср. техн.	Среднее
А1	А2	А3
Высокая	В1	12.21	10.89	9.90
Средняя	В2	16.28	14.52	13.20
Низкая	В3	8.51	7.59	6.90
Сумма по столбцам				Всего: 100

Критерий c²_эмп= (20-12.21)² ₊ (10-10.89)² ₊ (3-9.90)² ₊ (11-16.28)² ₊ (15-14.52)² ₊

12.21 10.89 9.90 16.28 14.52

₊ (18-13.20)² ₊ (6-8.51)² ₊ (8-7.59)² ₊ (9-6.90)² _{= 14.74}

13.20 8.51 7.59 6.90

_.Число степеней свободы n=(3-1)(3-1)=4. Критическое значение критерия при 95% доверительной вероятности составляет 9.49, при 99% - 13.28. Поскольку c²_эмп >c²_кр, то зависимость между уровнем образования и удовлетворенностью работой статистически значима (a=0.01).

Рассчитав эмпирическое значение критерия c², можно рассчитать коэффициенты Чупрова и Пирсона:

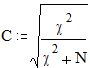
= 0.358,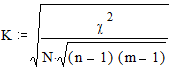

= 0.271.

Исследование связи между удовлетворенностью профессией и социальным положением испытуемых дало следующие результаты:

Таблица 24

Удовлетворенность профессиональной деятельностью	Социальное положение испытуемого	Суммы по строкам
Предпри-ниматели	Гос. служащие	Рабочие	Тружени-ки села
	А1	А2	А3	А4
Высокая	В1	10.25	10.66	11.48	8.61
Средняя	В2	7.75	8.06	13.20	8.68
Низкая	В3	7.00	7.28	7.84	5.88
Сумма по столбцам					Всего:100

Критерий c²_эмп= (14-10.25)² ₊ (13-10.66)² ₊ (6-11.48)² ₊ (8-8.61)² ₊

10.25 10.66 11.48 8.61

₊ (7-7.75)² ₊ (4-8.06)² ₊ (14-13.20)² ₊ (6-8.68)² ₊ (4-7.00)² ₊ (9-7.28)² ₊

7.75 8.06 13.20 8.68 7.00 7.28

₊ (8-7.84)² ₊ (7-5.88)² _{= 9.447}

7.84 5.88

Число степеней свободы n=(4-1)(3-1)=6. Критическое значение критерия при 95% доверительной вероятности составляет 12.592. Поскольку c²_эмп <c²_кр, то связь между удовлетворенностью профессией и социальным положением испытуемых статистически незначима (a=0.05).

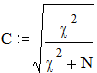
= 0.293,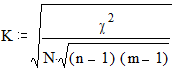

= 0.196.

Коэффициент многоклеточной сопряженности Пирсона С для зависимости «удовлетворенность профессией - образование» выше, чем для зависимости «удовлетворенность профессией - социальное положение», следовательно, в первой зависимости связь более тесная, чем во второй. Аналогичный вывод можно сделать и по коэффициенту Чупрова К.

Следует иметь также в виду, что с помощью рассмотренных коэффициентов и критериев доказывается только отличие распределения цифр в таблице от равномерного. Для описания же характера связи между явлениями следует использовать другие методы, о некоторых из них речь пойдет ниже.

8.2 Корреляционная связь

Корреляционная связь - это согласованное изменение двух или более признаков. Корреляционная связь означает, что изменчивость одного признака находится в некоторой связи с изменениями другого признака. Например, количество знаний человека, оцененное по какой-либо шкале, будет закономерно расти с увеличением его возраста. Количество ошибок при чтении текста или при решении задач будут закономерно уменьшаться при увеличении количества выполненных тренировочных упражнений. В зависимости от величины нагрузки на тренировках будут изменяться спортивные показатели спортсменов и так далее. Используется также термин корреляционная зависимость, который означает, что направленные изменения одного признака приводят к направленным изменениям другого. Термины корреляционная связь и корреляционная зависимость не являются синонимами, поскольку два признака, изменяющиеся согласованно, могут зависеть не друг от друга, а от какого-либо третьего признака. Например, количество церквей в городе и количество баров-ресторанов изменяются согласованно - в том городе, где много церквей, там много и баров. Связь же здесь не прямая, а опосредованная: больше памятников старины (церквей), следовательно, больше туристов, поэтому в городе больше баров и ресторанов. То есть корреляционная связь не является свидетельством причинно-следственной связи, а только показывает, что изменениям одного признака, как правило, соответствуют изменения другого. При корреляционной зависимости изменение одного признака непосредственно влияет на изменение другого: между количеством памятников старины в городе и количеством туристов есть корреляционная зависимость. Но в целом, если нет уверенности в причинно-следственной зависимости между двумя или более явлениями, то лучше пользоваться термином «корреляционная связь».

Корреляционные связи характеризуются формой, направлением и силой. По форме различаются связи прямолинейные и криволинейные. Прямолинейной может быть связь между количеством правильно решенных задач и количеством выполненных тренировочных заданий. А вот, например, связь между уровнем мотивации и эффективностью выполнения задачи криволинейная: эффективность выполнения задачи возрастает только до определенного, так называемого оптимального уровня мотивации, а затем начинает снижаться.

По направлению корреляционная связь может быть положительной (прямой) либо отрицательной (обратной). При положительной прямолинейной корреляции более высоким значениям одного признака соответствуют более высокие значения другого, а более низким значениям одного признака, соответственно более низкие другого. При отрицательной связи более высоким значениям одного признака соответствуют более низкие другого. Так, связь между количеством тренировочных заданий и количеством правильно решенных задач прямая (положительная), а между количеством тренировочных заданий и количеством допущенных ошибок - обратная (отрицательная).

Сила связи характеризует, насколько строго выполняется зависимость. Чем сильнее связь между явлениями, тем более сильно оказывается вытянутым облако точек на графике. Степень вытянутости облака оценивается с помощью коэффициента корреляции. Коэффициент корреляции изменяется от минус до плюс единицы. Знак показывает, является ли связь положительной или отрицательной, а абсолютная величина коэффициента корреляции - силу связи. Если коэффициент близок к нулю, то связь отсутствует, если близок к единице, то связь значима.

При классификации силы связи пользуются двумя шкалами. Общая шкала ориентирована на абсолютное значение коэффициента корреляции:

· сильная (тесная) связь ÷ r÷ >0.70

· средняя связь 0.50< ÷ r÷ <0.69

· умеренная связь 0.30< ÷ r÷ <0.49

· очень слабая связь (отсутствие связи) ÷ r÷ <0.29

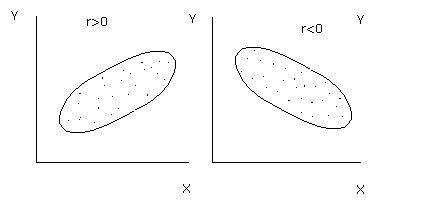
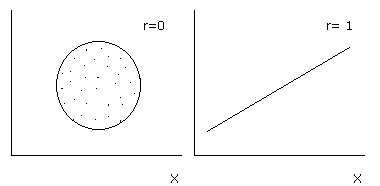
Рис.6. Возможные варианты расположения облака точек на графике и соответствующие им коэффициенты корреляции.

Частная классификация учитывает объем выборки и оценивает достоверность наличия корреляционной связи:

· высокая значимая корреляция при r, соответствующем уровню статистической значимости p<0.01

· значимая корреляция - при r, соответствующем уровню статистической значимости p<0.05

· тенденция достоверной связи при r, соответствующем уровню статистической значимости p<0.10

· корреляция незначима при r, не достигающим уровня статистической значимости.

Поскольку даже высокий коэффициент корреляции при малом объеме выборки может оказаться незначимым статистически, а при больших объемах выборки слабая связь статистически значима, то лучше пользоваться второй классификацией.

8.2.1 Меры связи для явлений, измеренных в ранговых шкалах

С помощью коэффициента ранговой корреляции Спирмена можно определить силу и направление связи между двумя признаками или двумя профилями (иерархиями) признаков. Формула в общем случае имеет следующий вид:

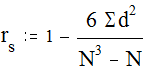
где d - разность между рангами каждой из переменных (ранжирование производится раздельно для каждой из переменных), а N - количество ранжируемых значений (или переменных, образующих иерархию). Полученное эмпирическое значение r_s сравнивается с критическими значениями, приведенными в таблицах (Таблица 10 Приложения). Если эмпирическое значение коэффициента ранговой корреляции больше критического или равно ему, то связь признается значимой.

Задача: По результатам тестирования учеников 10 класса одной из школ Ленинградской области оценить корреляцию между двумя иерархиями ценностей - шкалой важности ценностей и шкалой ценностей, которые легче достигнуть.

Таблица 25.

Оценка корреляционной связи между шкалой важности ценностей и шкалой ценностей, которые легче достигнуть, по результатам тестирования учеников 10 класса одной из школ Ленинградской области
№№ ценностей	Ранги важности ценностей (X)	Ранги доступности ценностей (Y)	di=Xi-Yi	di^2
			-6
			-6
			-5
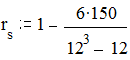
	=0,476

r_{s крит.}=0.50 (р=0.10). r_s < r_{s крит} Þ связь между шкалой ценностей, которые важнее, и шкалой ценностей, которые легче достигнуть, незначима.

При исследовании связи между различными признаками у одних и тех же испытуемых нередко два или более значений переменных получают один и тот же ранг. В этом случае в формулу коэффициента ранговой корреляции Спирмена вводятся поправки, и она принимает вид:

где Т_a,b - поправки, рассчитываемые по формулам

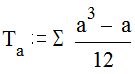
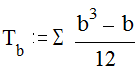
соответственно для первого (а) и второго (b) признака (второй иерархии). «a» и «b» - объем каждой группы одинаковых рангов: например, если два ранжируемых значения признака совпадают, то объем группы равен 2; если 3 значения совпадают - объем группы равен трем и т.д. При малых объемах групп поправка несущественна, при совпадении большого количества рангов она становится уже заметной.

Задача: Есть ли связь между способностью классификации и осведомленностью по тесту ШТУР у учениц 10 класса одной из школ Ленинградской области?

Таблица 26.

Оценка связи между способностью классификации и осведомленностью по тесту ШТУР у учениц 10 класса одной из школ Ленинградской области
Осведомленность	Ранг	Способность классификации	Ранг	di^2
	25,5			72,25
			23,5	56,25
			13,5	420,25
			13,5	306,25
	25,5			380,25
	19,5		32,5
			3,5	756,25
	25,5			6,25
			32,5	650,25
	25,5			56,25
			30,5	552,25
			3,5	756,25
	19,5			72,25
			13,5	72,25
	12,5		13,5
	3,5			210,25
	9,5			342,25
	19,5			2,25
	19,5			2,25
	25,5		23,5
	25,5			56,25
	12,5			42,25
	9,5			0,25
	19,5		23,5
	19,5		23,5
	15,5			156,25
	3,5			2,25
	15,5		30,5
	12,5			12,25
	12,5			132,25
	1,5		23,5
	1,5		23,5
Сумма:
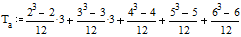
	=40		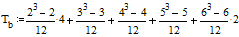=54
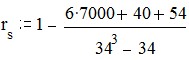
	= - 0.072

r_{s крит.}= 0.44 (0.01) r_s < r_{s крит}Þ

Ответ корреляционная связь между способностью классификации и осведомленностью по тесту ШТУР у учениц 10 класса незначима.

Дата добавления: 2014-12-27