В шкале интервалов или отношений 1 страница

Для явлений, измеренных в интервальных шкалах или в шкале отношений, наиболее распространенным является использование коэффициента линейной корреляции Пирсона, обозначаемого r_xy.

где x_i, y_i - значения случайных величин, измеренных на i-том объекте, М_х, М_у, s_х, s_у - средние арифметические и стандартные отклонения соответствующих случайных величин, N – количе-ство испытуемых. Коэффициент корреляции может принимать как положительные, так и отри-цательные значения от -1 до 1. Если значения близки к нулю, то корреляция отсутствует, значе-ния близки к 1 или -1 - корреляция сильная. Проверить достоверность отличия от нуля получен-ного значения коэффициента корреляции можно непосредственно по таблицам критических значений коэффициента линейной корреляции Пирсона (Таблица 11 Приложения) (коэффици-ент корреляции следует признать статистически значимым, если он превышает табличное критическое значение или равен ему) или с помощью критерия Стьюдента для мер связи.

Задача: Есть ли связь между способностью классификации и поиска аналогии по тесту ШТУР у учениц 10 класса одной из школ Ленинградской области?

Таблица 29

Оценка зависимости между показателями способностей классификации и поиска аналогии по тесту ШТУР у учеников 11 класса
способности классификации (х)	способности поиска аналогии (у)	Х-Мх	У-Му	(Х-Мх)×(У-Му)
			2,9	14,5
			-4,1	-20,5
			2,9	5,8
			-1,1	-5,5
			-0,1	-0,5
			-3,1	-6,2
			1,9	7,6
			2,9	8,7
			3,9	3,9
		-2	2,9	-5,8
		-3	-1,1	3,3
		-4	1,9	-7,6
		-1	0,9	-0,9
			2,9	8,7
		-2	-0,1	0,2
		-4	-2,1	8,4
		-5	-4,1	20,5
		-6	-1,1	6,6
		-6	-3,1	18,6
		-2	-3,1	6,2
Среднее 18	15,1			Сумма 66.0
Стандартное отклонение	3,934	2,673
	= 0.330	r кр.=0,444 (0.05) и 0,378 (0,10)

r_xy < r _кр Þ связь между показателями способностей классификации и поиска аналогии по тесту ШТУР у учеников 11 класса незначима.

Коэффициенты линейной корреляции Пирсона можно рассчитать с помощью встроенной функции Microsoft Excel. Для того чтобы воспользоваться встроенной функцией сначала необходимо переменные, между которыми будут рассчитываться коэффициенты корреляции, представить в виде единого массива, то есть расположить их в соседних столбцах таблицы данных. Затем следует войти в раздел «Анализ данных» из меню «Сервис», где выбрать подраздел «Корреляция». На экране высвечивается меню подраздела «Корреляция», в котором задаются входной интервал переменных и выходной интервал (номер левой верхней ячейки выходного интервала). Входной интервал переменных задается в виде единого массива, например «a1:b24» при двух переменных по 24 значения в каждой из выборок. Но с помощью встроенной функции Microsoft Excel можно рассчитать коэффициенты корреляции сразу между несколькими переменными. Если, к примеру, задать массив «a1:d16», то будут рассчитываться коэффициенты корреляции между четырьмя переменными по 16 значений в каждой: a1:a16, b1:b16, c1:c16 d1:d16. Выходные данные представляют собой матрицу коэффициентов корреляции между переменными.

8.3 Корреляционный анализ

Корреляционный анализ дает возможность оценки степени согласованности изменений (варьирования) большого числа признаков и выделить группы взаимокоррелирующих признаков. Результаты вычисления корреляций для некоторого набора признаков записываются в виде квадратной матрицы. В заголовки строк и столбцов выносятся названия или номерами признаков, в клетки таблицы заносятся коэффициенты корреляции каждого признака с каждым. Испытуемые и их порядковые номера в корреляционной матрице не представлены. Понятно, что по главной диагонали матрицы будут располагаться единицы, поскольку коэффициент корреляции любой величины с собой будет равен единице. Корреляционная матрица является симметричной относительно главной диагонали: коэффициенты корреляции признака Х с признаком У и признака У с признаком Х равны между собой. Поэтому, как правило, заполняется и используется только верхняя половина матрицы.

По приведенным в таблице 12 Приложений результатам ШТУР, показанным девушками- ученицами 10 класса одной из школ Ленинградской области (n=34), рассчитаны следующие коэффициенты корреляции:

Таблица 30.

Коэффициенты корреляции результатов учениц 10 класса по различным разделам теста ШТУР
	Столбец 1	Столбец 2	Столбец 3	Столбец 4	Столбец 5	Столбец 6
Столбец 1	1,00
Столбец 2	0,47	1,00
Столбец 3	0,26	0,00	1,00
Столбец 4	0,40	0,25	0,12	1,00
Столбец 5	0,54	0,23	-0,05	0,16	1,00
Столбец 6	0,08	0,04	-0,11	0,02	0,44	1,00

Примечание к таблицам 30-31: 1- общая осведомленность; 2- частная осведомленность; 3- способности классификации; 4- способности поиска аналогии; 5- способности обобщения; 6- способности выполнения счетных операций

Далее в таблице надо выделить коэффициенты корреляции, величина которых превышает критические значения для разных уровней достоверности, как правило, 90%, 95% и 99%. Такие значения выделяются либо шрифтом, либо подчеркиванием, либо цветом. Критические значения коэффициента корреляции Пирсона рассчитываются по критерию t-Стьюдента или берутся из таблицы критических значений с учетом числа испытуемых. Например, значения r, превышающие уровень достоверности 90% будем выделять подчеркиванием (но в нашей таблице таковых не оказалось), 95% - курсивом, 99%- жирным шрифтом. Значения, не отличающиеся значимо от нуля можно опустить. В окончательном виде матрица корреляций принимает следующий вид:

Таблица 31.

Коэффициенты корреляции результатов учениц 10 класса по различным разделам теста ШТУР
	Столбец 1	Столбец 2	Столбец 3	Столбец 4	Столбец 5	Столбец 6
Столбец 1
Столбец 2	0,47
Столбец 3
Столбец 4	0,40
Столбец 5	0,54
Столбец 6					0,44

По полученным данным строится так называемый корреляционный граф. Корреляционный граф - это фигура, состоящая из вершин и соединяющих их линий. В вершинах фигуры располагаются признаки, которые могут обозначаться их полными наименованиями, сокращениями либо цифрами. Линии, соединяющие вершины, характеризуют корреляционную связь между этими признаками. Тип линии отражает знак и достоверность отличия от нуля соответствующего коэффициента корреляции. Отсутствие линии, соединяющей признаки, говорит, что коэффициент корреляции данных признаков не отличается значимо от нуля. Форму корреляционного графа исследователь задает самостоятельно. Если признаков так много, что их трудно отобразить на одном корреляционном графе, то граф разделяется на части, которые называются корреляционными плеядами. Для нашей корреляционной матрице мы можем построить достаточно простой корреляционный граф, состоящий из одной плеяды (цифры в кружках соответствуют номерам признаков в таблице 31).

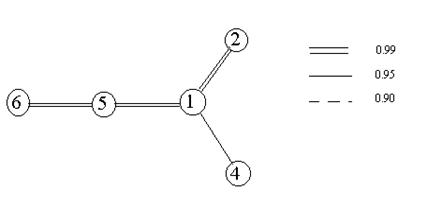
Рис.7. Корреляционный граф для результатов ШТУР учениц 10 класса.

Ниже аналогичным образом обработаны данные, характеризующие внимание, память и некоторые другие характеристики школьников(n=40):

Таблица 32.

Исходная корреляционная матрица:

№ переменной
	Устойчивость внимания	1,00	0,92	0,76	0,17	0,02	0,68	0,64	0,57	-0,21
	Объем внимания	0,92	1,00	0,82	0,19	0,02	0,74	0,67	0,55	-0,36
	Память	0,76	0,82	1,00	-0,06	0,07	0,77	0,49	0,63	-0,39
	Конфликтность	0,17	0,19	-0,06	1,00	0,64	0,21	0,13	0,18	-0,24
	Агрессивность	0,02	0,02	0,07	0,64	1,00	0,00	-0,11	0,10	0,11
	Абстрактность мышления	0,68	0,74	0,77	0,21	0,00	1,00	0,70	0,85	-0,50
	Успеваемость	0,64	0,67	0,49	0,13	-0,11	0,70	1,00	0,53	-0,26
	Креативность мышления	0,57	0,55	0,63	0,18	0,10	0,85	0,53	1,00	-0,47
	Ригидность мышления	-0,21	-0,36	-0,39	-0,24	0,11	-0,50	-0,26	-0,47	1,00

Таблица 33.

Окончательный вид корреляционной матрицы:

№ переменной
	Устойчивость внимания	1,00	0,92	0,76			0,68	0,64	0,57
	Объем внимания		1,00	0,82			0,74	0,67	0,55	- 0,36
	Память			1,00			0,77	0,49	0,63	-0,39
	Конфликтность				1,00	0,64
	Агрессивность					1,00
	Абстрактность мышления						1,00	0,70	0,85	-0,50
	Успеваемость							1,00	0,53
	Креативность мышления								1,00	-0,47
	Ригидность мышления									1,00

Рис.6. Корреляционный граф для результатов исследования психологических характеристик школьников.

Интерпретация результатов корреляционного анализа заключается в объяснении наличия и силы связей (или их отсутствия) на основе теоретических положений и здравого смысла. Так, интерпретируя полученные данные, следует обсудить причины появления тесной положительной связи характеристик внимания учащихся (устойчивость и объем внимания) и мышления (абстрактность и креативность мышления) между собой, а также с их памятью и успеваемостью; объяснить, почему ригидность мышления с большинством из перечисленных характеристик обнаруживает отрицательную корреляцию, а такие характеристики учащихся, как конфликтность и агрессивность, тесно связанные между собой, не проявляют связи с особенностями умственной деятельности и успеваемости.

При интерпретации результатов следует помнить, что наличие корреляционной связи не говорит о причинно-следственной зависимости между признаками. Поэтому иногда могут появиться такие связи, которые не удается объяснить без дополнительных исследований.

Более полный и математически обоснованный анализ корреляционных связей признаков выполняется на ЭВМ методами факторного анализа и главных компонент, которые выходят за рамки курса. Расчеты методами главных компонент и факторного анализа выполняются по программе MathCad («Statistics») или любой другой современной программе. Описание методов и рекомендации по их применению легко найти в литературе по предмету.

Список использованной литературы:

Анастази А. Психологическое тестирование. Кн.2. М., 1982

Ашмарин И.П., Васильев Н.Н., Амбросов В.А. Быстрые методы статистической обработки и планирование экспериментов. Изд. ЛГУ, Ленинград, 1971.

Дэвис С. Дж. Статистический анализ данных в геологии. т.1. М., «Недра», 1990.

Еремеев Б.А. Статистические процедуры при психологическом изучении текста. Учебное пособие. СПб, «Образование», 1996.

Машков В.Н. Основы дифференциальной психологии. Спб, изд. СПбГУ, 1998.

Сидоренко Е.В. Методы математической обработки в психологии. СПб., 1996

Тарасов С.Г. Математические методы в психологии. Учебно-методические указания. СПб.,1998, 56 с.

Дополнительная литература:

Гласс Дж., Стенли Дж. Статистические методы в педагогике и психологии. М., 1976.

Иберла К. Факторный анализ. М., 1980.

Суходольский Г.В. Основы математической статистики для психологов. Л., 1972.

Суходольский Г.В. Математическая психология. СПб., 1997.

Приложение 1. Таблицы критических значений.

Таблица 1.

Значения кумулятивной функции распределения

стандартного нормального распределения

Стандартное отклонение от среднего значения	Кумулятивная вероятность	Стандартное отклонение от среднего значения	Кумулятивная вероятность	Стандартное отклонение от среднего значения	Кумулятивная вероятность
-3.0	0.0014	-0.9	0.1841	1.1	0.8643
-2.9	0.0019	-0.8	0.2119	1.2	0.8849
-2.8	0.0026	-0.7	0.2420	1.3	0.9032
-2.7	0.0035	-0.6	0.2743	1.4	0.9192
-2.6	0.0047	-0.5	0.3085	1.5	0.9332
-2.5	0.0062	-0.4	0.3446	1.6	0.9452
-2.4	0.0082	-0.3	0.3821	1.7	0.9554
-2.3	0.0107	-0.2	0.4207	1.8	0.9641
-2.2	0.0139	-0.1	0.4602	1.9	0.9713
-2.1	0.0179	0.0	0.5000	2.0	0.9773
-2.0	0.0228	0.1	0.5398	2.1	0.9821
-1.9	0.0287	0.2	0.5793	2.2	0.9861
-1.8	0.0359	0.3	0.6179	2.3	0.9893
-1.7	0.0446	0.4	0.6554	2.4	0.9918
-1.6	0.0548	0.5	0.6915	2.5	0.9938
-1.5	0.0668	0.6	0.7257	2.6	0.9953
-1.4	0.0808	0.7	0.7580	2.7	0.9965
-1.3	0.0968	0.8	0.7881	2.8	0.9974
-1.2	0.1151	0.9	0.8159	2.9	0.9981
-1.1	0.1357	1.0	0.8413	3.0	0.9986
-1.0	0.1587

Таблица 2.

Таблица критических значений параметра «а» для исключения выскакивающих значений

	а	а
N	Уровень достоверности 95%	Уровень достоверности 99%
	0.941	0.988
	0.765	0.889
	0.642	0.780
	0.560	0.698
	0.507	0.637
	0.468	0.590
	0.437	0.555
	0.412	0.527
	0.392	0.502
	0.376	0.482
	0.338	0.438
	0.300	0.391
	0.281	0.367
	0.260	0.341

Таблица 3.

Таблица критических значений критерия c² Пирсона

Число степеней свободы	0,05	0,01	Число степеней свободы	0,05	0,01
	3,841	6,635		30,144	36,191
	5,991	9,210		31,410	37,566
	7,813	11,341		32,671	38,932
	9,488	13,277		33,924	40,289
	11,070	15,086		35,172	41,638
	12,592	16,812		36,415	42,980
	14,067	18,475		37,652	44,314
	15,507	20,090		38,885	45,642
	16,919	21,666		40,113	46,963
	18,307	23,209		41,337	48,278
	18,675	24,725		42,557	49,588
	21,026	26,217		43,773	50,892
	22,362	27,688		55,76	63,69
	23,685	29,141		67,50	76,15
	24,996	30,578		79,08	88,38
	26,296	32,000		90,53	100,43
	27,587	33,409		101,88	112,33
	28,869	34,805		113,15	124,12
				124,34	135,81

Таблица 4.

Критические значения F-критерия Фишера

с n₁ и n₂ степенями свободы при a=0.05

	n1=n1-1
n2=n2-1							¥
	3.18	3.14	3.07	3.01	2.94	2.90	2.86
	3.02	2.98	2.91	2.84	2.77	2.74	2.70
	2.90	2.85	2.79	2.72	2.65	2.61	2.57
	2.80	2.75	2.69	2.62	2.54	2.51	2.47
	2.71	2.67	2.60	2.53	2.46	2.42	2.48
	2.65	2.60	2.53	2.46	2.39	2.35	2.31
	2.59	2.54	2.48	2.40	2.33	2.29	2.25
	2.54	2.49	2.42	2.35	2.28	2.24	2.19
	2.49	2.45	2.38	2.31	2.23	2.19	2.15
	2.46	2.41	2.34	2.27	2.19	2.15	2.11
	2.42	2.38	2.31	2.23	2.16	2.11	2.07
	2.39	2.35	2.28	2.20	2.12	2.08	2.04
	2.37	2.32	2.25	2.18	2.10	2.05	2.01
	2.34	2.30	2.23	2.15	2.07	2.03	1.98
	2.32	2.27	2.20	2.13	2.05	2.01	1.96
	2.30	2.25	2.18	2.11	2.03	1.98	1.94
	2.28	2.24	2.16	2.09	2.01	1.96	1.92
	2.27	2.22	2.15	2.07	1.99	1.95	1.90
	2.25	2.20	2.13	2.06	1.97	1.93	1.88
	2.24	2.19	2.12	2.04	1.96	1.91	1.87
	2.22	2.18	2.10	2.03	1.94	1.90	1.85
	2.21	2.16	2.09	2.01	1.93	1.89	1.84
	2.12	2.08	2.00	1.92	1.84	1.79	1.74
	2.04	1.99	1.92	1.84	1.75	1.70	1.65
	1.96	1.91	1.83	1.75	1.66	1.61	1.55
¥	1.88	1.83	1.75	1.67	1.57	1.52	1.46

Таблица 5

Таблица критических значений t-критерия Стьюдента.

Число степеней	Уровень значимости
свободы	Односторонний критерий
	a=0,05	0,025	0,01	0,005	0,001	0,0005
	Двусторонний критерий
	a=0,10	0,05	0,02	0,01	0,002	0,001
	6,314	12,71	31,82	63,66	318,3	636.6
	2,920	4,303	6,965	9,925	22,33	31,60
	2,353	3,182	4,541	5,841	10,21	12,92
	2,132	2,776	3,747	4,604	7,173	8,610
	2,015	2,571	3,365	4,032	5,893	6,869
	1,943	2,447	3,143	3,707	5,208	5,959
	1,895	2,365	2,998	3,499	4,785	5,408
	1,860	2.306	2,896	3,355	4,501	5,041
	1,833	2,262	2,821	3,250	4,297	4,781
	1,812	2,228	2,764	3,169	4,144	4,587
	1,796	2,201	2,718	3,106	4,025	4,437
	1,782	2.179	2,681	3,055	3,930	4,318
	1,771	2,160	2,650	3,012	3,852	4,221
	1,761	2,145	2,624	2,977	3,787	4,140
	1,753	2,131	2,602	2,947	3,733	4,073
	1,746	2,120	2,583	2,921	3,686	4,015
	1,740	2,110	2,567	2,898	3,646	3,965
	1,734	2,101	2,552	2,878	3,610	3,922
	1,729	2,093	2,539	2,861	3,579	3,883
	1,725	2,086	2,528	2,845	3,552	3,850
	1,721	2,080	2,518	2,831	3,527	3,819
	1,717	2,074	2,508	2,819	3,505	3,792
	1,714	2,069	2,500	2,807	3,485	3,767
	1,711	2.064	2,492	2,797	3,467	3,745
	1,708	2,060	2,485	2,787	3,450	3,725
	1,706	2,056	2,479	2,779	3,435	3,707
	1,703	2,052	2,473	2,771	3,421	3,690
	1,701	2,048	2,467	2,763	3,408	3,674
	1,699	2,045	2,462	2,756	3,396	3,659
	1,697	2,042	2,457	2,750	3,385	3,646
Ґ	1,645	1,960	2,326	2,576	3,090	3,291

Таблица 6.

Дата добавления: 2014-12-27