
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
V. Исследование функций и построение их графиков
|
|
|
|
Общая схема исследования функции:
1. Нахождение области определения функции.
2. Исследование функции на четность.
3. Исследование функции на периодичность.
4. Нахождение асимптот.
5. Отыскание точек пересечения графика с осями координат.
6. Исследование функции с помощью первой производной.
7. Исследование функции с помощью второй производной.
8. Построение графика.
1. Совокупность всех значений, которые может принимать аргумент x функции f (x), называется областью определенияэтой функции.
При нахождении области определения функции следует помнить, что:
1. знаменатель дроби не может равняться нулю;
2. корень четной степени извлекается только из неотрицательного выражения;
3. функция, стоящая под знаком логарифма, должна быть положительной.
Пример 21. Найти область определения функции  .
.
Область определения x - 3 >0, т.е. x >3.
Пример 22. Найти область определения функции  .
.
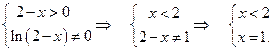
Т.е., область определения этой функции 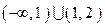 .
.
2. Функция f (x) называется чётной, если
1) область определения функции 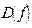 симметрична относительно 0,
симметрична относительно 0,
2) для всех  , f (– x) = f (x).
, f (– x) = f (x).
График четной функции симметричен относительно оси OY. Примерами четных функций могут служить  ,
, 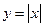 ,
,  .
.
Функция f (x) называется нечётной, если
1) область определения  симметрична относительно 0,
симметрична относительно 0,
2) для любого  f (– x) = – f (x).
f (– x) = – f (x).
График нечётной функции симметричен относительно начала координат. Примерами нечетных функций являются  ,
, 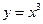 .
.
Если функция не является ни четной, ни нечетной, то она называется функцией общего вида. Так, функция  не является ни четной, ни нечетной, так как ее область определения
не является ни четной, ни нечетной, так как ее область определения  несимметрична относительно 0.
несимметрична относительно 0.
Для функции общего вида
либо 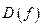 не является симметричной относительно нуля,
не является симметричной относительно нуля,
либо 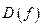 симметрична относительно нуля, но ни одно из равенств
симметрична относительно нуля, но ни одно из равенств
f (– x) = f (x), f (– x) = – f (x) не выполняется для всех  .
.
Пример 23. Исследовать на четность функцию 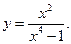
Так как 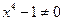 , то
, то  , т.е.
, т.е.  симметрична относительно нуля.
симметрична относительно нуля.
 .
.
Следовательно, эта функция является четной.
Пример 24. Исследовать на четность функцию 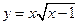 .
.
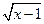 существует, если
существует, если  . Следовательно,
. Следовательно, 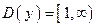 . Это множество не является симметричным относительно нуля, поэтому функция
. Это множество не является симметричным относительно нуля, поэтому функция 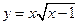 является функцией общего вида.
является функцией общего вида.
Пример 25. Исследовать на четность функцию 
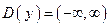 - множество симметричное относительно нуля.
- множество симметричное относительно нуля.
 Следовательно, функция
Следовательно, функция  является нечетной.
является нечетной.
3. Функция 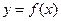 называется периодической, если существует такое постоянное число T > 0, что:
называется периодической, если существует такое постоянное число T > 0, что:
1) для всех 
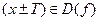 ,
,
2) для всех х из области определения функции 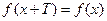 .
.
Если функция имеет конечное число точек разрыва, то она не является периодической.
Если функция принимает какое-то значение лишь конечное число раз, то она не является периодической.
Если область определения функции ограничена сверху и (или) снизу, то функция не является периодической.
Пример 26. Исследовать на периодичность функцию 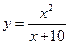 .
.
Найдем  Т.е. функция имеет лишь одну точку разрыва, следовательно, не является периодической.
Т.е. функция имеет лишь одну точку разрыва, следовательно, не является периодической.
Пример 27. Исследовать на периодичность функцию 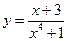 .
.
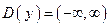 . Данная функция равна нулю только в точке x = -3, следовательно, не является периодической.
. Данная функция равна нулю только в точке x = -3, следовательно, не является периодической.
Пример 28. Исследовать на периодичность функцию 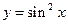 .
.
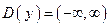 . Найдем Т из уравнения f (x +T) = f (x).
. Найдем Т из уравнения f (x +T) = f (x).
 . Т.е.
. Т.е. 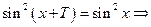


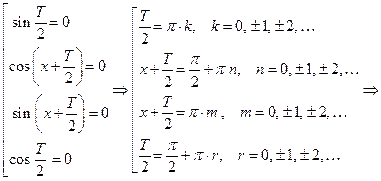

Итак, периодом могут быть числа: 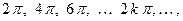
 Наименьший положительный период равен
Наименьший положительный период равен  .
.
4. Асимптотой называется прямая линия, к которой приближается график функции, когда точка графика неограниченно удаляется от начала координат. Различаются два вида асимптот: вертикальные и наклонные.
Вертикальной асимптотой графика функции 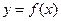 , называется вертикальная прямая x = a, если
, называется вертикальная прямая x = a, если 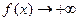 или
или  при каком-либо из условий:
при каком-либо из условий:  ,
, 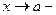 ,
,  .
.
График функции  может иметь вертикальную асимптоту x = a, если а – точка разрыва или, если D(f) является множеством числовой оси, ограниченным справа или слева точкой а. Если
может иметь вертикальную асимптоту x = a, если а – точка разрыва или, если D(f) является множеством числовой оси, ограниченным справа или слева точкой а. Если  , то вертикальных асимптот нет.
, то вертикальных асимптот нет.
Пример 29. Найти вертикальные асимптоты графика функции 
Найдем D(f). Так как  и
и  , то
, то  .
.
Следовательно, могут существовать две вертикальные асимптоты x = -1 и х = 0.
 , т.е., х = -1 вертикальной асимптотой не является.
, т.е., х = -1 вертикальной асимптотой не является.
 ,
, 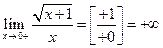 . Следовательно, прямая х = 0 является вертикальной асимптотой.
. Следовательно, прямая х = 0 является вертикальной асимптотой.

Прямая y = kx + b является наклонной асимптотой для графика функции y = f (x), если 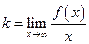 ,
,  .
.
Если хотя бы один из этих пределов не существует или равен ∞, то наклонной асимптоты график не имеет.
Если k = 0, то получаем горизонтальную асимптоту.
Для функций, содержащих логарифмическую, показательную функции, arctg x, arcctg x, необходимо исследовать отдельно ситуации  и
и 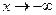 .
.
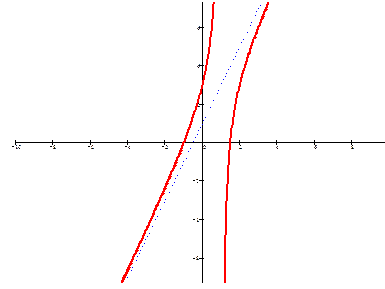
Пример 30. Найти наклонные асимптоты графика функции 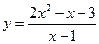 .
.
 ,
,

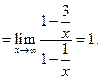
Итак,  – наклонная асимптота. Заметим, что асимптоты обычно изображают пунктирной линией.
– наклонная асимптота. Заметим, что асимптоты обычно изображают пунктирной линией.
5. Для того чтобы найти точку пересечения графика с осью OY, необходимо вычислить значение  . Чтобы найти точки пересечения графика с осью OX, нужно найти корни уравнения
. Чтобы найти точки пересечения графика с осью OX, нужно найти корни уравнения  (или убедиться в отсутствии корней). Уравнение
(или убедиться в отсутствии корней). Уравнение  часто не удаётся решить точно, но даже приближенные значения корней помогают лучше уяснить строение графика.
часто не удаётся решить точно, но даже приближенные значения корней помогают лучше уяснить строение графика.
Пример 31. Найти точки пересечения графика функции  с осями координат.
с осями координат.
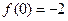 . Следовательно, точка (0, -2) является точкой пересечения функции с осью OY.
. Следовательно, точка (0, -2) является точкой пересечения функции с осью OY.
 . Корнями этого уравнения являются
. Корнями этого уравнения являются  и
и  . Это значит, что график функции пересекает ось OX в точках (-1, 0) и (2, 0).
. Это значит, что график функции пересекает ось OX в точках (-1, 0) и (2, 0).
6. Исследование функции с помощью первой производной можно провести по следующей схеме:
1) Найти производную 
2) Найти точки “подозрительные на экстремум”, то есть точки, в которых производная f¢ (x) равна нулю или не существует.
3) Выяснить знак производной в каждом из интервалов, на которые полученные точки делят числовую ось.
4) Если при переходе слева направо через точку x производная меняет знак с «+» на «-», то в точке x функция имеет максимум, если с «-» на «+», - минимум. Если знак производной не меняется, то экстремума в точке x нет.
 Чтобы наглядно увидеть, есть ли в исследуемой точке экстремум и какого вида, отмечаем точки на оси ОХ. Если на интервале производная положительна, то функция возрастает. Этот факт отмечаем стрелкой
Чтобы наглядно увидеть, есть ли в исследуемой точке экстремум и какого вида, отмечаем точки на оси ОХ. Если на интервале производная положительна, то функция возрастает. Этот факт отмечаем стрелкой  , направленной вверх. Если производная отрицательна, то функция убывает, тогда рисуем стрелку
, направленной вверх. Если производная отрицательна, то функция убывает, тогда рисуем стрелку  , направленную вниз. Все стрелки направлены слева направо, т.е. в ту же сторону что и ось ОХ.
, направленную вниз. Все стрелки направлены слева направо, т.е. в ту же сторону что и ось ОХ.
Например, если получается схема

то в точке х 1 функция имеет максимум, в точке х2 – минимум, в точке
х 3 экстремума нет.
5. Вычислить максимальные и минимальные значения функции.
Пример 32. Найти экстремумы функции 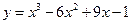 .
.

 при
при  т.е. при
т.е. при 
Решая это квадратное уравнение, найдём корни  . Нанесём эти точки на числовую ось. Получим три интервала
. Нанесём эти точки на числовую ось. Получим три интервала 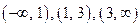 . Определим знаки производной на этих промежутках. Для этого выберем по произвольному числу в каждом из интервалов и подставим их в выражение для производной.
. Определим знаки производной на этих промежутках. Для этого выберем по произвольному числу в каждом из интервалов и подставим их в выражение для производной.
На промежутке 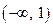 выберем точку x =0.
выберем точку x =0. 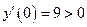 , следовательно, на этом интервале функция возрастает. На промежутке (1; 3) выберем точку x = 2.
, следовательно, на этом интервале функция возрастает. На промежутке (1; 3) выберем точку x = 2. 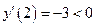 , следовательно, функция на (1; 3) убывает. На промежутке (3,
, следовательно, функция на (1; 3) убывает. На промежутке (3, 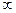 ) выберем точку x = 4.
) выберем точку x = 4.  , значит функция на (3,
, значит функция на (3, 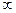 ) возрастает.
) возрастает.
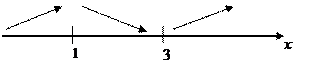
Получаем схему

Итак, максимальное значение y (1) = 3, минимальное значение y (3) = -1.
7. Исследование функции с помощью второй производной можно провести по следующей схеме:
1. Найти 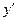 и
и  .
.
2. Найти точки, в которых  равна нулю или не существует, и нанести эти точки на числовую ось.
равна нулю или не существует, и нанести эти точки на числовую ось.
3. Найти знаки второй производной на каждом из полученных интервалов.
4. Если 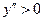 , то график функции является выпуклым вниз
, то график функции является выпуклым вниз  , если
, если 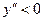 , то -выпуклым вверх
, то -выпуклым вверх  .
.
5. Если точка  и
и  при переходе через точку
при переходе через точку 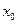 меняет знак, то находят
меняет знак, то находят 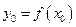 . В этом случае
. В этом случае  – точка перегиба графика функции.
– точка перегиба графика функции.
Пример 33. Исследовать с помощью второй производной функцию 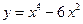 .
.
Найдем  .
. 
Найдем точки, в которых  .
.
 .
.
Нанесем точки  и
и  , на числовую ось и определим знак
, на числовую ось и определим знак  на интервалах
на интервалах 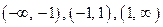 , для чего возьмем по произвольной точке из каждого интервала.
, для чего возьмем по произвольной точке из каждого интервала.
 ,
,
 ,
,
 .
.
Получаем схему

Точки 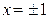 принадлежат D(y). Найдем y (1) и у (-1).
принадлежат D(y). Найдем y (1) и у (-1).
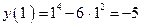 ,
,
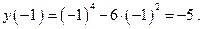
Т.е. (-1; -5) и (1; -5) – точки перегиба графика функции.

8. Построение графика.При построенииграфика функции сначала наносят асимптоты, которые являются «скелетом» графика. Затем отмечают характерные точки: экстремумы, точки перегиба, точки пересечения с осями. Если функция четная или нечетная, график можно строить только для x > 0, а затем отобразить симметрично относительно оси OY или начала координат соответственно. В случае периодической функции можно строить график на промежутке, длина которого равна наименьшему периоду, а затем периодически продолжить его на всю ось.
Пример 34. Провести полное исследование функции  и построить ее график.
и построить ее график.
1. Область определения функции: 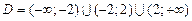
2. Т.к. область определения симметрична относительно нуля, то следует проверить функцию на четность.
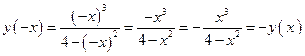 , т.е. функция является нечетной. Её график симметричен относительно начала координат, поэтому проводить исследование можно лишь для
, т.е. функция является нечетной. Её график симметричен относительно начала координат, поэтому проводить исследование можно лишь для 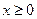 .
.
3. Т.к. точек разрыва всего две и, следовательно, они не образуют “периодического множества” на числовой оси, то и функция не является периодической.
4. Найдем асимптоты графика функции. Вертикальной асимптотой на промежутке 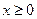 может служить лишь прямая х = 2.
может служить лишь прямая х = 2.
 ,
, 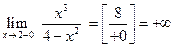 .
.
Т.к. пределы равны 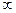 , график имеет при
, график имеет при 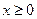 вертикальную асимптоту
вертикальную асимптоту 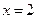 . В силу нечетности функции
. В силу нечетности функции  также является вертикальной асимптотой.
также является вертикальной асимптотой.
Проверим наличие наклонной асимптоты  . Найдем k и b, где
. Найдем k и b, где
 ,
,  .
.
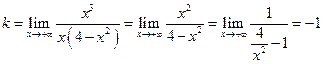 ,
,
 Следовательно, уравнение наклонной асимптоты
Следовательно, уравнение наклонной асимптоты 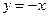 .
.
5. График пересекает ось Y при  , при этом
, при этом 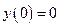 , т.е. график проходит через точку
, т.е. график проходит через точку  . Т.к.
. Т.к.  только при
только при  , то других точек пересечения с осью OX нет.
, то других точек пересечения с осью OX нет.
6. Исследуем функцию с помощью первой производной.

Приравняем к нулю числитель и знаменатель дроби и нанесем полученные в промежутке 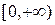 точки на числовую ось.
точки на числовую ось.
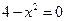 =>
=>  ,
, 
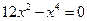
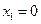 и
и  ,
, 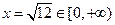 .
.
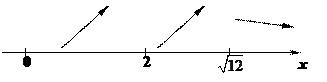
Определяем знаки производной на участках  . Если
. Если  , то функция возрастает. Нарисуем на этом участке стрелку, идущую вправо - вверх (т.е. в направлении оси ОХ и вверх), если
, то функция возрастает. Нарисуем на этом участке стрелку, идущую вправо - вверх (т.е. в направлении оси ОХ и вверх), если 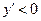 , то функция убывает – стрелка идет вправо вниз.
, то функция убывает – стрелка идет вправо вниз.
При переходе через точку 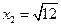 производная меняет знак с «+» на «–», следовательно, в этой точке функция имеет максимум.
производная меняет знак с «+» на «–», следовательно, в этой точке функция имеет максимум.
В этой точке  .
.
При переходе через точку 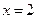 , производная не меняет знак, функция возрастает слева и справа от этой точки.
, производная не меняет знак, функция возрастает слева и справа от этой точки.
7. Исследуем функцию на выпуклость.


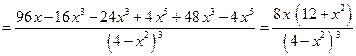 .
.
Приравняем к нулю числитель и знаменатель дроби и нанесем полученные в промежутке  точки на числовую ось.
точки на числовую ось.

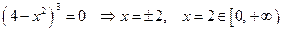 .
.
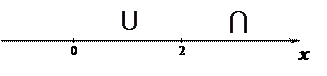 |
Определяем знак
 в полученных промежутках (0, 2) и (2, +∞). Там, где
в полученных промежутках (0, 2) и (2, +∞). Там, где 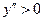 , функция выпукла вниз – рисуем дугу
, функция выпукла вниз – рисуем дугу  , а там, где
, а там, где 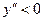 функция выпукла вверх – рисуем дугу
функция выпукла вверх – рисуем дугу  .
.
9. Строим график функции на [0, 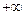 ).
).
Прежде всего, пунктирной линией наносим асимптоты 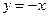 и
и 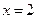 .
.
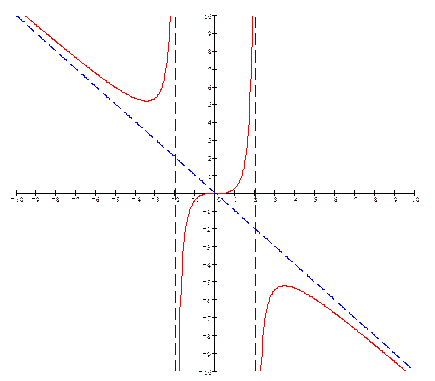
К этим линиям будут стремиться точки графика, удаляясь от начала координат. На промежутке [0, 2) функция выпукла вниз и возрастает. На промежутке (2, +∞) функция выпукла вверх, возрастает на  и убывает на
и убывает на  , приближаясь к асимптоте
, приближаясь к асимптоте 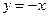 . Построив график на [0, +∞), строим симметрично относительно (0, 0) график на (-∞, 0].
. Построив график на [0, +∞), строим симметрично относительно (0, 0) график на (-∞, 0].
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 3349; Нарушение авторских прав?; Мы поможем в написании вашей работы!