Принципы моделирования

Классификация систем по типу поведения

Где

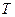– упорядоченное по возрастанию множество моментов времени,

– множество значений составляющих вектора состояния,

– множество значений составляющих вектора входа,

– класс допустимых входных функций,

– множество значений составляющих вектора выхода,

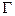– класс допустимых выходных функций,

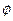– переходная функция состояния,

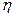– функция выхода.

Общее абстрактное описание (абстрактная модель) лишь отражает характер описания и общие свойства систем широкого класса с различным типом поведения. Для построения модели удобнее использовать некоторые типовые математические схемы, отражающие те или иные типы поведения реальных моделируемых систем.

В этом отношении, следуя [6], можно представить классификацию систем по типу поведения в виде схемы, представленной на рисунке 1.1.

По числу состояний модели делятся на статические и динамические. Для статических моделей характерным является то, что выход системы (или ее характеристики) в некоторый момент времени определяется значением входного сигнала в тот же момент времени: .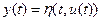

В плане абстрактного описания эти системы можно определить как системы с одним значением состояния, то есть «предыстория» не изменяет состояния и, стало быть, не влияет на выход. Если возможных состояний множество, то систему (и модель) классифицируют как динамическую.

Динамические модели (системы) следует различать по времени перехода их из состояния в состояние, что обычно определяется характером множества Т значений времени, которое интересует исследователя. Если Т – счетное множество значений, то имеет место описание в дискретном времени и модель (систему) называют моделью (системой) с дискретным временем.

Соответственно, если Т – несчетное множество, то – моделью (системой) с непрерывным временем.

По типу состояний (по типу множества значений Х) системы (модели) разделяют на системы (модели) с дискретным состоянием, если множество Х есть конечное счетное множество, и на системы (модели) с непрерывным состоянием, если Х – несчетное множество (множество обладает мощностью континуума).

По условиям переходов систем из состояния в состояние они могут быть разделены на детерминированные и стохастические.

Если модель путем применения к ней формальных процедур позволяет однозначно предсказать изменение состояния и, соответственно, выхода, то модель называют детерминированной.

Если удается оценить лишь статистические характеристики этих переменных, то модель называют стохастической. Такие модели обычно имеют место при необходимости учета различного рода случайных факторов, таких как случайные входы, случайные параметры, случайные начальные условия, с целью отражения присущей моделируемой реальной системе неопределенности поведения, или неполноты информации о системе.

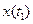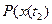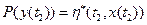В этом отношении абстрактная модель по Калману описывает детерминированную модель. Рассмотреть вероятностные динамические модели (условные марковские процессы), у которых текущее состояние и входное воздействие определяют не , а вероятностное распределение и, возможно, текущее состояние определяет не , а вероятностное распределение , можно, задавая переходную функцию и функцию выхода в виде и , соответственно.

Моделирование – это замещение исследуемого объекта (оригинала) его условным образом или другим объектом (моделью) и изучение свойств оригинала путем исследования свойств модели.

Действительная польза от моделирования может быть получена только при соблюдении следующих условий:

· модель должна обеспечивать корректное (или, как говорят, адекватное) отображение свойств оригинала, существенных с точки зрения исследуемой стороны его поведения;

· модель должна позволять устранить проблемы, присущие проведению исследований при реальном объекте.

Принципы моделирования, в сжатой форме отражают достаточно богатый опыт, который накоплен к настоящему времени в области разработки и использования математических моделей. Отметим следующие основные принципы.

Принцип информационной достаточности. При полном отсутствии информации об исследуемой системе построение ее модели невозможно. При наличии полной информации о системе ее моделирование лишено смысла. Существует некоторый критический уровень априорных сведений о системе, при достижении которого может быть построена ее адекватная модель.

Принцип осуществимости. Создаваемая модель должна обеспечивать достижение поставленной цели исследования с вероятностью, существенно отличающейся от нуля и за конечное время.

Принцип множественности. Создаваемая модель должна отражать в первую очередь те свойства реальной системы (или явления), которые влияют на выбранный показатель эффективности. Поэтому для более полного исследования модели часто используют ряд моделей, позволяющих с разных сторон отражать рассматриваемый процесс.

Принцип агрегирования. В большинстве случаев сложную систему можно представить состоящей из агрегатов (подсистем), для адекватного математического описания которых оказываются пригодными некоторые стандартные математические схемы. Этот принцип позволяет достаточно гибко перестраивать модель в зависимости от задач исследования.

Принцип параметризации. В ряде случаев моделируемая система имеет в свом составе относительно изолируемые подсистемы, характеризующиеся определенным параметром. Такие системы можно заменять в модели соответствующими числовыми величинами, а не описывать процесс их функционирования. Данный принцип позволяет сократить объем и продолжительность моделирования, не снижая существенно адекватность модели.

Степень реализации перечисленных принципов в каждой конкретной модели может быть различной и зависит как от пожеланий разработчика, так и от соблюдения им технологии моделирования. А любая технология моделирования предполагает наличие определенной последовательности действий.

Для компьютерного моделирования – математического моделирования с использованием средств вычислительной техники, характерна следующая последовательность действий:

1) определение цели моделирования;

2) разработка концептуальной модели – абстрактной модели, определяющей структуру моделируемой системы, свойства ее элементов и причинно-следственные связи, присущие системе и существенные для достижения цели моделирования;

3) формализация модели;

4) программная реализация модели;

5) планирование модельных экспериментов;

6) реализация плана эксперимента;

7) анализ и интерпретация результатов моделирования.

Сразу нужно оговорить, что в данной работе не рассматривается область, связанная с планированием модельных экспериментов.

Дата добавления: 2014-12-27