
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Контрольной работы № 1
|
|
|
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ
КОНТРОЛЬНАЯ РАБОТА № 1
Задание 1
Решите систему уравнений методом Крамера, методом обратной матрицы
1.1. 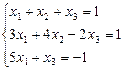 1.2.
1.2. 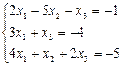
1.3. 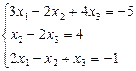 1.4.
1.4. 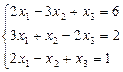
1.5. 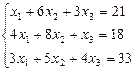 1.6.
1.6. 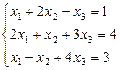
1.7. 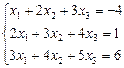 1.8.
1.8. 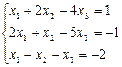
1.9. 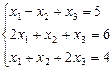 1.10.
1.10. 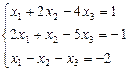
Задание 2
Решите систему уравнений методом Гаусса
2.1. 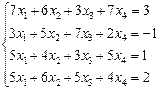 2.2.
2.2. 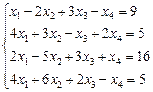
2.3. 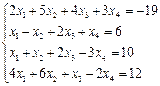 2.4.
2.4. 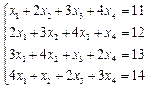
2.5. 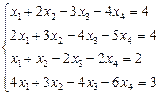 2.6.
2.6. 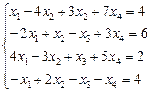
2.7. 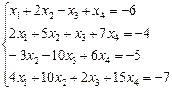 2.8.
2.8. 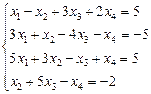
2.9. 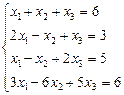 2.10.
2.10. 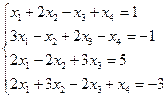
Задание 3
Даны вершины треугольника А 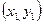 , В
, В 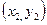 , С
, С 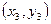 . Составьте: уравнение медианы и высоты, проведенной из вершины А. Сделайте чертеж.
. Составьте: уравнение медианы и высоты, проведенной из вершины А. Сделайте чертеж.
А(-6;13), В(-13;-11), С(3;1); А(-2;1), В(2;2), С(26;-5)
А(-11;15), В(-18;-9), С(-2;3); А(7;9), В(2,-3), С(3;6)
А(3;0), В(-5;6),С(-4;1); А(10;2), В(2;8), С(3;3)
А(10;2), В(2;8),С(3;3); А(6;2), В(-2;8), С(-1;3)
А(8;3), В(0;9), С(1;4); А(5;-1), В(-3;5), С(-2;0)
Задание 4
Найти пределы
4.1  а)
а) 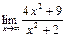 б)
б) 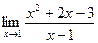 в)
в) 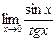
4.2. а) 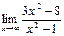 б)
б) 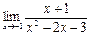 в)
в) 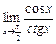
4.3. а) 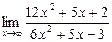 б)
б) 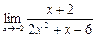 в)
в) 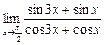
4.4. а) 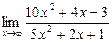 б)
б) 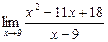 в)
в) 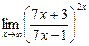
4.5. а) 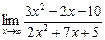 б)
б) 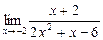 в)
в) 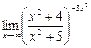
4.6. а) 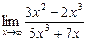 б)
б) 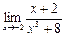 в)
в) 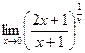
4.7. а) 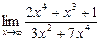 б)
б) 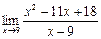 в)
в) 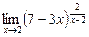
4.8. а) 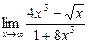 б)
б) 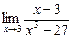 в)
в) 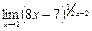
4.9. а) 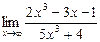 б)
б) 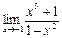 в)
в) 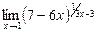
4.10. а) 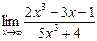 б)
б) 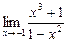 в)
в) 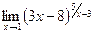
Задание 5
Найти производные функций
5.1. а) 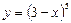 б)
б) 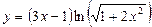
в) 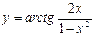
5.2. а) 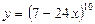 б)
б) 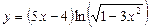
в) 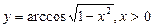
5.3. а) 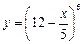 б)
б) 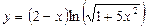
в) 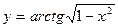
5.4. а) 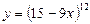 б)
б) 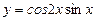
в) 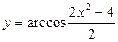
5.5. а) 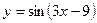 б)
б) 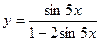
в) 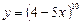
5.6. а) 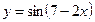 б)
б) 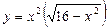
в) 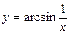
5.7. а) 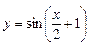 б)
б) 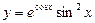
в) 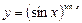
5.8. а) 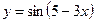 б)
б) 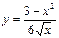
в) 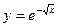
5.9. а) 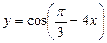 б)
б) 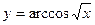
в) 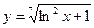
5.10. а) 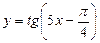 б)
б) 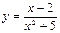
в) 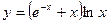
Задание 6
Исследуйте функции, найдите асимптоты графиков функций и постройте графики функций
6.1. 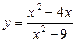 6.2.
6.2. 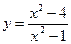 6.3.
6.3. 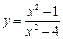 6.4.
6.4. 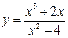
6.5. 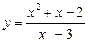 6.6.
6.6. 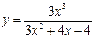 6.7.
6.7. 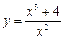
6.8. 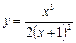 6.9.
6.9. 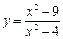 6.10.
6.10. 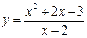
Задание 7
Найти интегралы
7.1. а) 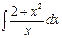 б)
б) 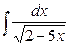
7.2. а) 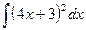 б)
б) 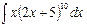
7.3. а) 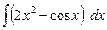 б)
б) 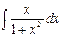
7.4. а) 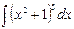 б))
б)) 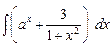
7.5. а) 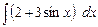 б))
б)) 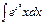
7.6. а) 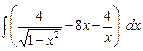 б)
б) 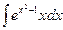
7.7. а) 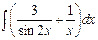 б)
б) 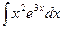
7.8. а) 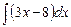 б)
б) 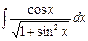
7.9. а) 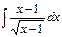 б)
б) 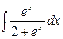 7.10. а)
7.10. а) 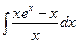 б)
б) 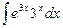
Задание 8
Найти стационарные точки, точки экстремума и экстремумы функций
8.1. 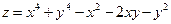 ; 8.2.
; 8.2. 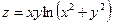
8.3. 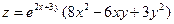 ; 8.4.
; 8.4. 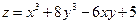
8.5. 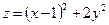 ; 8.6.
; 8.6. 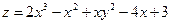

8.7. 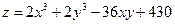 ; 8.8.
; 8.8. 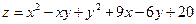
8.9. 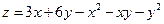 ; 8.10.
; 8.10. 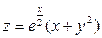
Задание 9
Найти общее решение дифференциального уравнения
9.1. 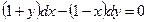 ;
;
9.2. 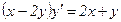 ;
;
9.3. 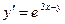
9.4. 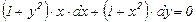 ;
;
9.5. 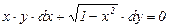
9.6. 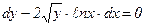
9.7. 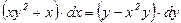
9.8. 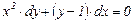
9.9. 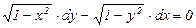
9.10. 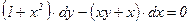
Контрольная работа выполняются по индивидуальным вариантам. Вариант соответствует последней цифре зачетной книжки студента, если последняя цифра 0, следует выполнять десятый вариант. Домашняя контрольная работа на проверку предоставляется за две недели до начала сессии. Однако этот срок являются крайним. Чтобы работа была своевременно прорецензирована, при необходимости доработана и сдана повторно, ее надлежит представить значительно раньше указанного срока.
Если в ходе написания работы у студента появляются вопросы или затруднения в решении задач контрольной работы, он может обратиться в филиал за консультацией. При выполнении контрольных работ необходимо соблюдать следующие правила:
1. В работу должны быть включены все задачи, указанные в задании, строго по своему варианту. Контрольные работы, содержащие не все задачи задания, а также содержащие задачи не своего варианта, не зачитываются.
2. Перед решением каждой задачи нужно привести полностью ее условие;
3. Задания следует решать в той последовательности, в какой они даны, строго соблюдая при этом нумерацию заданий;
4. Не допускается замена задач контрольной работы другими;
5. Решение заданий должно сопровождаться пояснениями; нужно привести в общем виде используемые формулы с объяснением используемых обозначений;
6. Работа может быть выполнена в школьной тетради, либо на листах формата А4;
7. Титульный лист оформляется в соответствии с приложением.
Если работа получила в целом положительную оценку (зачет), то студент допускается к зачету. Если работа не зачтена, ее необходимо в соответствии с требованиями преподавателя частично или полностью переделать. Повторную работу надо выполнить в той же тетради (если есть место) или в новой тетради и вместе с не зачтенной работой сдать снова на проверку.
Задание 1
Решить систему линейных уравнений методом Крамера и методом обратной матрицы.
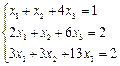
а) метод Крамера
Решение:
Находим определитель матрицы:
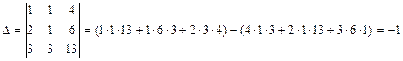
Находим определители матриц, полученных из матрицы А заменой соответственно первого, второго и третьего столбцов свободных членов.

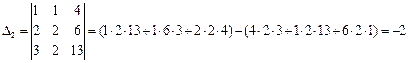
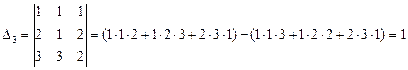
По формулам Крамера:
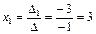 ;
; 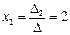 ;
; 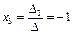
б) метод обратной матрицы
Решение:
Обозначим: 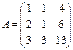 ;
; 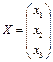 ;
; 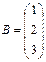 .
.
Тогда в матричной форме система имеет вид: 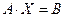 .
.
Определитель матрицы 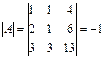 , значит обратная матрица существует. По правилу нахождения обратной матрицы находим
, значит обратная матрица существует. По правилу нахождения обратной матрицы находим 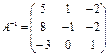
Умножим матричное уравнение на 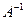 , получаем:
, получаем:
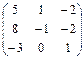
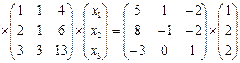
окончательно имеем:
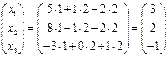 , значит
, значит 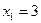 ;
; 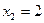 ;
; 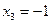 .
.
Задание 2
Решить систему линейных уравнений методом Гаусса
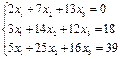
Решение:
Рассмотрим первое уравнение системы и проведем преобразования относительно переменной  . Исключим данную переменную из второго и третьего уравнений. Для этого прибавим к ним первое уравнение, умноженное соответственно на
. Исключим данную переменную из второго и третьего уравнений. Для этого прибавим к ним первое уравнение, умноженное соответственно на 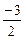 и
и 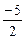 .
.
Получим:
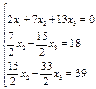
Рассмотрим второе уравнение полученной системы и проведем преобразования относительно переменной 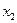 . Исключим данную переменную из третьего уравнения. Для этого умножим второе уравнение на
. Исключим данную переменную из третьего уравнения. Для этого умножим второе уравнение на 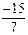 .
.
Получим:
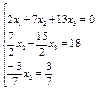
Третье уравнение данной системы содержит одну переменную, второе – две, первое – три. Прямой ход метода Гаусса закончен, обратным ходом получаем:
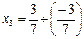 ;
; 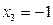 ;
; 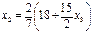 ;
; 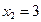 ;
;
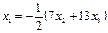 ;
; 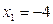
Итак, решением данной системы будет: 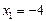 ,
, 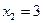 ,
, 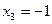
Задание 3
Точки А(2,1), В(1,-2), С(-1,0) являются вершинами треугольника АВС.Найти уравнения сторон треугольника АВС. Найти уравнение одной из медиан треугольника АВС. Найти уравнение одной из высот треугольника АВС.
Решение:
Найдем уравнения сторон треугольника АВС
Первая прямая проходит через две точки А(2,1), В(1,-2), поэтому ее уравнение будем искать в виде 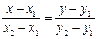 .
.
Подставляя x1=2, x2=1, y1=1, y2=-2,
получим: 
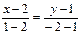 ;
; 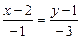 ;
; 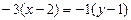 ; отсюда уравнение первой прямой имеет вид:
; отсюда уравнение первой прямой имеет вид: 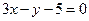
Вторая прямая проходит через две точки В(1,-2), С(-1,0) поэтому ее уравнении
будем искать в виде: 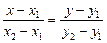 .
.
Подставляя x1 = 1, x2 = -1, y1= -2, y2= 0,
получим: 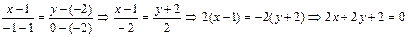 , разделим на 2 получим x+y+1=0.
, разделим на 2 получим x+y+1=0.
Третья прямая проходит через две точки А(2,1), С(-1,0) поэтому ее уравнение будем искать в виде: 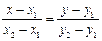 . Подставляя x1 = 2, x2 =-1, y1=1, y2= 0,
. Подставляя x1 = 2, x2 =-1, y1=1, y2= 0,
получим:
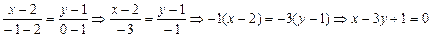
Найдем уравнение одной из медиан треугольника АВС.
Обозначим середину стороны ВС буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.
B(1;-2), C(-1;0)
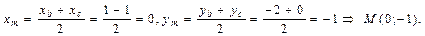 Уравнение медианы АM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана АМ проходит через точки А (2;1) и М(0;-1), поэтому:
Уравнение медианы АM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана АМ проходит через точки А (2;1) и М(0;-1), поэтому:
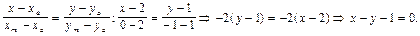
Найдем уравнение одной из высот треугольника АВС.
Найдем уравнение высоты CZ, проходящей через точку
С(-1;0) и точку Z, лежащую на стороне АВ: 3x-y-5=0. Для этого найдем угловой коэффициент k1 прямой АВ. Для этого представим уравнение
3x-y -5 = 0 в виде (2): y = k 1 x + b.
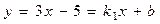 , т.е. k1 = 3.
, т.е. k1 = 3.
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых (8): k1 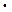 k = -1. Подставляя вместо k1 угловой коэффициент данной прямой,получим:
k = -1. Подставляя вместо k1 угловой коэффициент данной прямой,получим: 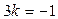 ,
, 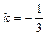 . Так как перпендикуляр проходит через точку С(-1;0) и имеет
. Так как перпендикуляр проходит через точку С(-1;0) и имеет
k =- 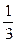 , то будем искать его уравнение в виде: y-y0 =k(x-x0). Подставляя x 0 = -1, k = -
, то будем искать его уравнение в виде: y-y0 =k(x-x0). Подставляя x 0 = -1, k = - 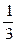 , y0=0 получим: y - 0 =-
, y0=0 получим: y - 0 =- 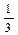 (x –(-1)) x +3y + 1 = 0. - уравнение высоты CZ.
(x –(-1)) x +3y + 1 = 0. - уравнение высоты CZ.
Задание 4
а) Вычислить предел 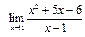 .
.
Решение:
Если подставить 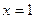 в рассматриваемую функцию, получим ноль в числителе и знаменателе. Без дополнительных преобразований трудно сказать, к чему будет стремиться подобное выражение. Поэтому такие выражения называют неопределенностью вида
в рассматриваемую функцию, получим ноль в числителе и знаменателе. Без дополнительных преобразований трудно сказать, к чему будет стремиться подобное выражение. Поэтому такие выражения называют неопределенностью вида 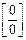 . Разложим на множители числитель, для этого решим уравнение
. Разложим на множители числитель, для этого решим уравнение 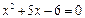 ,
, 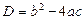 ,
, 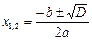 D=49,
D=49, 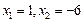 Числитель раскладывается на множители
Числитель раскладывается на множители 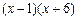 . Имеем
. Имеем 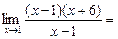
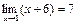
б) Вычислить предел 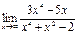
Решение:
Имеем неопределенность вида 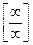 . Для раскрытия этой неопределенности разделим числитель и знаменатель на наивысшую степень переменной
. Для раскрытия этой неопределенности разделим числитель и знаменатель на наивысшую степень переменной 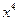
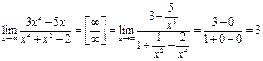
в) Найти предел функции 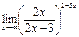
Решение:
Имеем неопределенность вида 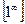 . Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом
. Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом 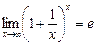 .
.
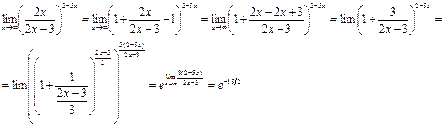
Задание 5
а) Найти 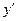 , если
, если 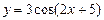 .
.
Решение:
Последовательно применяя правило дифференцирования сложной функции, получим: 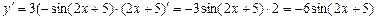
Производная функции равна 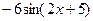
б) Используя правила вычисления производных и таблицу,
найдите производные следующих функций:
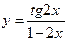
Решение: 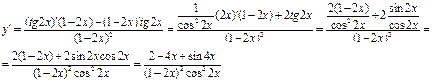
Производная заданной функции равна 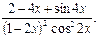
в) Найти производную функции 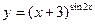
Решение:
Прологарифмируем левую и правую части функции. 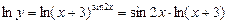 Вычислим производную логарифмической функции:
Вычислим производную логарифмической функции:
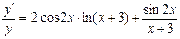 ;
; 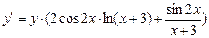 ; Подставим в выражение заданное значение y, окончательно имеем, производная функции равна:
; Подставим в выражение заданное значение y, окончательно имеем, производная функции равна:
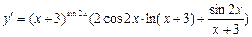
Задание 6
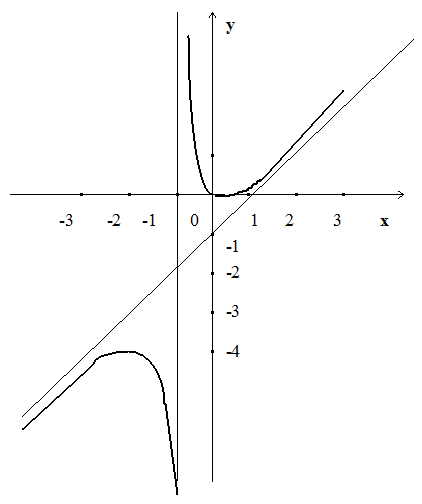
Исследовать функцию 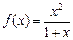 и построить ее график.
и построить ее график.
Решение:
Данная функция определена и непрерывна на всей оси ОХ, за исключением точки 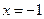 , где она терпит бесконечный разрыв. Следовательно, прямая
, где она терпит бесконечный разрыв. Следовательно, прямая 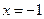 является вертикальной асимптотой. Поскольку
является вертикальной асимптотой. Поскольку 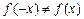 и
и 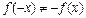 , то рассматриваемая функция не является ни четной, ни нечетной, то есть это функция общего вида. Точка (0,0) является точкой пересечения функции с осями координат.
, то рассматриваемая функция не является ни четной, ни нечетной, то есть это функция общего вида. Точка (0,0) является точкой пересечения функции с осями координат.
Вычислим производную: 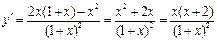 .
.
Производная обращается в ноль при 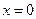 и
и 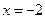 .Построим интервалы монотонности:
.Построим интервалы монотонности:
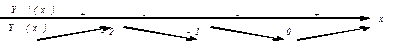
Функция возрастает при 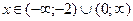 и убывает при
и убывает при 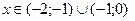 . Точка
. Точка 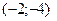 ─ точка максимума, а точка
─ точка максимума, а точка 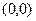 ─ точка минимума функции. Найдем вторую производную:
─ точка минимума функции. Найдем вторую производную:
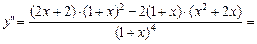
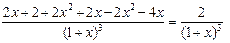 .
.
Вторая производная в нуль нигде не обращается, но при переходе через точку 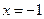 меняет свой знак с минуса на плюс. Следовательно, в интервале
меняет свой знак с минуса на плюс. Следовательно, в интервале 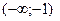 график функции выпуклый, а в интервале
график функции выпуклый, а в интервале 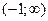 - вогнутый. Точек перегиба функция не имеет.
- вогнутый. Точек перегиба функция не имеет.
Выясним, имеет ли функция наклонные асимптоты. 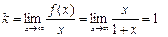 ,
,
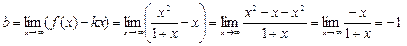 .
.
Следовательно, прямая 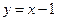 является наклонной асимптотой при
является наклонной асимптотой при 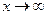 . Легко проверить, что эта же прямая является наклонной асимптотой при
. Легко проверить, что эта же прямая является наклонной асимптотой при 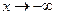 .
.
Построим график исследуемой функции:
Задание 7
а) Вычислить неопределенный интеграл:
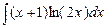
Решение:
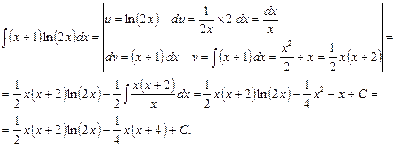
Заданный неопределенный интеграл равен 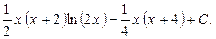
б) Вычислить неопределенный интеграл: 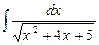
Решение:
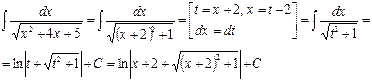
Заданный неопределенный интеграл равен 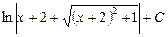 .
.
в) Вычислить неопределенный интеграл: 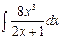
Решение:
Положим t=2x+1, тогда 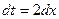 , и следовательно,
, и следовательно, 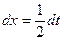 . Так как
. Так как 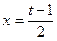 , то
, то
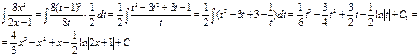
Задание 8
Найти стационарные точки и экстремумы функции 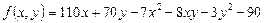
Решение:
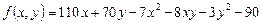
Найдем первые частные производные функции 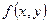 :
:
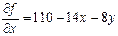 ,
, 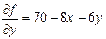 . Найдем стационарные точки графика функции
. Найдем стационарные точки графика функции 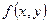 . Для этого решим систему:
. Для этого решим систему:
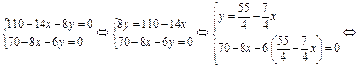
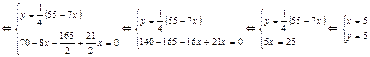
Следовательно 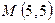 - стационарная точка. Проверим ее на экстремум, для этого
- стационарная точка. Проверим ее на экстремум, для этого
введем обозначения: 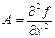 ,
, 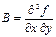 ,
, 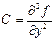 , тогда
, тогда 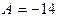 ,
, 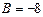 ,
, 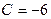 ,
, 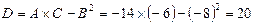 .
.
Т.к. 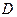 > 0, то экстремум есть, а т.к.
> 0, то экстремум есть, а т.к. 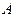 < 0, то это максимум. Следовательно, при
< 0, то это максимум. Следовательно, при 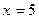 и
и 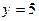 , функция достигает максимального значения:
, функция достигает максимального значения:
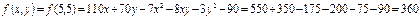
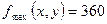 при
при 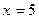 и
и 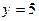 .
.
Задание 9
а) Решить уравнение: 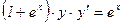
Решение:
Так как 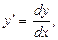 то
то 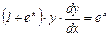 . Разделим обе части на 1+ ех, получим:
. Разделим обе части на 1+ ех, получим:
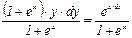 ;
; 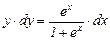 . Интегрируя, находим:
. Интегрируя, находим:
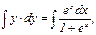
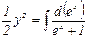 ;
; 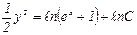 ;
; 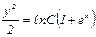
После потенцирования получим решение: 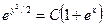 ;
;
б) Решить уравнение 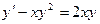
Решение:
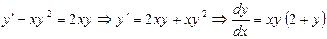 . Разделив обе части на
. Разделив обе части на 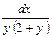 , получим
, получим 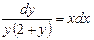 . Проинтегрируем полученное уравнение
. Проинтегрируем полученное уравнение 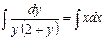 . Представим
. Представим 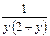 , как
, как 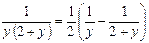 , тогда
, тогда
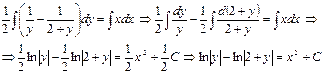
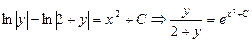
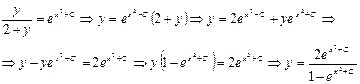
Решением данного уравнения является 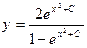 .
.
в) Решить уравнение: 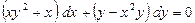
Решение:
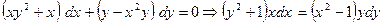 . Разделив обе части на
. Разделив обе части на 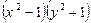 , получим
, получим 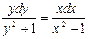 . Проинтегрируем полученное уравнение:
. Проинтегрируем полученное уравнение:
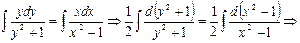
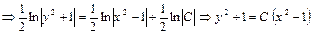
Решением данного уравнения является 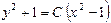 .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 448; Нарушение авторских прав?; Мы поможем в написании вашей работы!