Абсолютные, относительные и средние показатели в статистике

Статистический показатель – это количественно выраженное определенное свойство, качество совокупности в целом и ее частей.

По статистической структуре показатели системы можно условно разделить на три группы: абсолютные (объемные) величины, относительные величины и средние величины.

Первичная статистическая информация выражается прежде всего в виде абсолютных показателей, которые являются количественной базой всех форм учета. Абсолютные показатели характеризуют итоговую численность единиц совокупности или ее частей, размеры (объемы, уровни) изучаемых явлений и процессов, выражают временные характеристики. Абсолютные показатели могут быть только именованными числами, где единица измерения выражается в конкретных цифрах. В зависимости от сущности исследуемого явления и поставленных задач единицы измерения могут быть натуральными, условно-натуральными, стоимостными и трудовыми [9].

Натуральные единицы измерения соответствуют потребительским или природным свойствам товара или предмета и оцениваются в физических мерах массы, длины, объема (килограмм, тонна, метр и т.д.).

Разновидностью натуральных единиц выступают условно-натуральные, которые используются в тех случаях, если продукт, имея несколько разновидностей, должен переводиться в условный продукт с помощью специальных коэффициентов (молочные продукты с разным содержанием сливочной основы, мыло с разным содержанием жирных кислот и т.д.).

Стоимостные единицы измерения оценивают социально-экономические процессы и явления в денежном выражении (цены, сопоставимые цены), что очень важно в условиях рыночной экономики.

Вся совокупность абсолютных величин включает как индивидуальные показатели (характеризуют значения отдельных единиц совокупности), так и суммарные показатели (характеризуют итоговое значение нескольких единиц совокупности или итоговое значение существенного признака по той или иной части совокупности).

Абсолютные показатели следует также подразделить на моментные и интервальные. Моментные абсолютные показатели характеризуют факт наличия явления или процесса, его размер (объем) на определенную дату времени.

Интервальные абсолютные показатели характеризуют итоговый объем явления за тот или иной период времени (например, выпуск продукции за квартал или за год и т. д.), допуская при этом последующее суммирование.

Абсолютные показатели не могут дать исчерпывающего представления об изучаемой совокупности или явлении, поскольку не могут отразить структуру, взаимосвязи, динамику. Данные функции выполняют относительные показатели, которые определяются на основе абсолютных показателей.

В статистике относительные показатели используют в сравнительном анализе и в обобщении. Относительные показатели - это цифровые обобщающие показатели, они есть результат сопоставления двух статистических величин. По своей природе относительные величины производны от деления текущего (сравниваемого) абсолютного показателя на базисный показатель.

Относительные показатели могут быть получены или как соотношения одноименных статистических показателей, или как соотношения разноименных статистических показателей. В первом случае получаемый относительный показатель рассчитывается или процентах, или в относительных единицах, или в промилле (в тысячных долях). Если соотносятся разноименные абсолютные показатели, то относительный показатель в большинстве случаев бывает именованным. Каждая относительная величина представляет собой дробь, ее числителем является величина, которую хотят сравнить, а знаменателем - величина, с которой производится сравнение. Знаменатель относительной величины называют базой сравнения. База сравнения может приниматься за 1, 100, 1000 или за 10000 единиц, и тогда относительная величина будет выражена соответственно десятичной дробью, в процентах (%), в промилле (%₀) и продецимилле (%₀₀).

Если сравниваемая величина в два и более раза больше базы сравнения, то лучше выражать относительную величину десятичной дробью. В тех случаях, когда результат сравнения близок к единице, относительную величину выражают в процентах. Если же результат сравнения намного меньше единицы, то относительную величину часто выражают в промилле или продецимилле.

Используемые статистикой относительные величины можно классифицировать следующим образом.

А. Отношения между одноименными показателями:

1) относительные величины структуры;

2) относительная величина координации;

3) относительная величина планового задания;

4) относительные величины выполнения плана;

5) относительные величины динамики;

6) относительные величины сравнения;

Б. Отношения между разноименными показателями.

1) относительная величина интенсивности.

Остановимся на отдельных видах относительных величин. Отношения между одноименными показателями представляют собой относительные величины, не имеющие размерности. Они выражаются чаще всего в процентах, а в случаях, когда относительная величина больше двух, - целым числом с десятичной дробью.

Относительная величина структуры (ОВС) характеризует структуру совокупности, определяет долю (удельный вес) части в общем объеме совокупности. ОВС рассчитывают как отношение объема части совокупности к абсолютной величине всей совокупности, определяя тем самым удельный вес части в общем объеме совокупности (%):

, (1.4)

где m_i - объем исследуемой части совокупности; M - общий объем исследуемой совокупности.

Относительная величина координации (ОВК) характеризует соотношение между двумя частями исследуемой совокупности, одна из которых выступает как база сравнения (%):

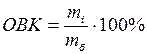, (1.5)

где m_i - одна из частей исследуемой совокупности; m_б - часть совокупности, которая является базой сравнения.

Относительная величина планового задания (ОВПЗ) используется для расчета в процентном отношении увеличения (уменьшения) величины показателя плана по сравнению с базовым уровнем в предшествующем периоде, для чего используется формула:

, (1.6)

где Р_пл - плановый показатель; Р ₀ - фактический (базовый) показатель в предшествующем периоде.

Относительная величина выполнения плана (ОВВП) характеризует степень выполнения планового задания за отчетный период (%) и рассчитывается по формуле:

, (1.7)

где Р_ф - величина выполнения плана за отчетный период; Р_пл - величина плана за отчетный период.

Относительная величина динамики (ОВД) характеризует изменение объема одного и того же явления во времени в зависимости от принятого базового уровня. ОВД рассчитывают как отношение уровня анализируемого явления или процесса в текущий момент времени к уровню этого явления или процесса за прошедший период времени. В результате мы получаем коэффициент роста, который выражается кратным отношением. При исчислении этой величины в процентах (результат умножается на 100) получаем темп роста.

Темпы роста можно просчитывать как с постоянным базовым уровнем (базисные темпы роста - ОВД_б), так и с переменным базовым уровнем (цепные темпы роста - ОВД_ц):

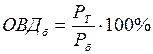, (1.8)

где Р_Т - уровень текущий; Р_б - уровень базисный;

, (1.9)

где Р_Т - уровень текущий; Р_Т-1 - уровень, предшествующий текущему.

Относительная величина сравнения (ОВС_р) - соотношение одноименных абсолютных показателей, относящихся к разным объектам, но к одному и тому же времени (например, соотносятся темпы роста населения в разных странах за один и тот же период времени):

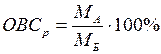, (1.10)

где М_А - показатель первого одноименного исследуемого объекта; М_Б - показатель второго одноименного исследуемого объекта (база сравнения).

Все предыдущие показатели относительных величин характеризовали соотношения одноименных статистических объектов. Однако есть группа относительных величин, которые характеризуют соотношение разноименных, но связанных между собой статистических показателей. Эту группу называют группой относительных величин интенсивности (ОВИ), которые выражаются, как правило, именованными числами. В статистической практике относительные величины интенсивности применяются при исследовании степени объемности явления по отношению к объему среды, в которой происходит распространение этого явления. ОВИ здесь показывает, сколько единиц одной совокупности (числитель) приходится на одну, на десять, на сто единиц другой совокупности (знаменатель).

Примерами относительных величин интенсивности могут служить, скажем, показатели уровня технического развития производства, уровня благосостояния граждан, показатели обеспеченности населения средствами массовой информации, предметами культурно-бытового назначения и т.д. ОВИ рассчитывается по формуле:

, (1.11)

где А - распространение явления; В_А - среда распространения явления А.

Средние величины используются на этапе обработки и обобщения полученных первичных статистических данных. Потребность определения средних величин связана с тем, что у различных единиц исследуемых совокупностей индивидуальные значения одного и того же признака, как правило, неодинаковы.

Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности.

Если исследуется совокупность с качественно однородными признаками, то средняя величина выступает здесь как типическая средняя. Например, для групп работников определенной отрасли с фиксированным уровнем дохода определяется типическая средняя расходов на предметы первой необходимости, т.е. типическая средняя обобщает качественно однородные значения признака в данной совокупности, каковым является доля расходов у работников данной группы на товары первой необходимости.

При исследовании совокупности с качественно разнородными признаками на первый план может выступить нетипичность средних показателей. Такими, к примеру, являются средние показатели произведенного национального дохода на душу населения (разные возрастные группы), средние показатели урожайности зерновых культур по всей территории России (районы разных климатических зон и разных зерновых культур), средние показатели рождаемости населения по всем регионам страны, средние температуры за определенный период и т.д. Здесь средние величины обобщают качественно разнородные значения признаков или системных пространственных совокупностей (международное сообщество, континент, государство, регион, район и т.д.) или динамических совокупностей, протяженных во времени (век, десятилетие, год, сезон и т.д.). Такие средние величины называют системными средними.

Таким образом, значение средних величин состоит в их обобщающей функции. Средняя величина заменяет большое число индивидуальных значений признака, обнаруживая общие свойства, присущие всем единицам совокупности. Это, в свою очередь, позволяет избежать случайных причин и выявить общие закономерности, обусловленные общими причинами.

На этапе статистической обработки могут быть поставлены самые различные задачи исследования, для решения которых нужно выбрать соответствующую среднюю.

Средние величины бывают простые и взвешенные. Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте.

Введем следующие условные обозначения:

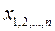- величины, для которых исчисляется средняя;

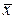- средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений;

f_i – вес (статистический вес или вес средней), показывающий сколько раз встречается i- e значение осредняемого признака в совокупности.

Различные средние выводятся из общей формулы степенной средней:

, (1.12)

при k = 1 - средняя арифметическая; k = -1 - средняя гармоническая; k → 0 - средняя геометрическая; k = 2 - средняя квадратическая.

Виды степенных средних и формулы для их расчетов приведены в таблице 1.4.

Таблица 1.4 - Виды степенных средних

Вид степенной средней	Показатель степени (k)	Формула расчета
Простая	Взвешенная
Арифметическая
Гармоническая	-1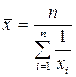
Геометрическая
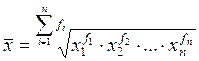
Квадратическая
Кубическая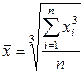

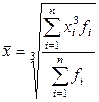
Средняя арифметическая - самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности.

Формула средней арифметической (простой) имеет вид:

, (1.13)

где n - численность совокупности.

Например, средняя заработная плата работников предприятия вычисляется как средняя арифметическая:

.

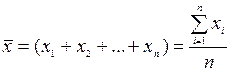Определяющими показателями здесь являются заработная плата каждого работника и число работников предприятия. При вычислении средней общая сумма заработной платы осталась прежней, но распределенной как бы между всеми работниками поровну. К примеру, необходимо вычислить среднюю заработную плату работников небольшой фирмы, где заняты 8 человек:

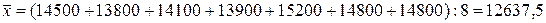(рублей).

При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании средней арифметической взвешенной, которая имеет вид:

. (1.14)

Так, нам необходимо рассчитать средний курс акций какого-то акционерного общества на торгах фондовой биржи. Известно, что сделки осуществлялись в течение 5 дней (5 сделок), количество проданных акций по курсу продаж распределилось следующим образом:

1010 рублей - 800 акций;

990 рублей - 650 акций;

1015 рублей - 700 акций;

900 рублей - 550 акций;

1150 рублей - 850 акций.

Исходным соотношением для определения среднего курса стоимости акций является отношение общей суммы сделок (ОСС) к количеству проданных акций (КПА):

ОСС = 1010·800+990·650+1015·700+900·550+1150·850= 3 634 500;

КПА = 800+650+700+550+850=3550.

В этом случае средний курс стоимости акций, рассчитанный по формуле средней арифметической взвешенной, будет равен:

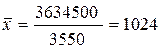(рублей).

Необходимо знать свойства арифметической средней, что очень важно как для ее использования, так и при ее расчете.

1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты.

Другими словами, постоянный множитель может быть вынесен за знак средней.

2. Если от каждой варианты отнять (прибавить) какое-либо произвольное число, то новая средняя уменьшится (увеличится) на то же число.

3. Если каждую варианту умножить (разделить) на какое-то произвольное число, то средняя арифметическая увеличится (уменьшится) во столько раз.

4. Если все частоты (веса) разделить или умножить на какое-либо число, то средняя арифметическая от этого не изменится.

5. Сумма отклонений отдельных вариантов от средней арифметической всегда равняется нулю.

Средняя гармоническая. Эту среднюю называют обратной средней арифметической.

Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы (1.12), подставив k = -1:

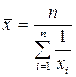. (1.15)

К примеру, нам нужно вычислить среднюю скорость двух автомашин, прошедших один и тот же путь, но с разной скоростью: первая - со скоростью 100 км/ч, вторая - 90 км/ч. Применяя метод средней гармонической, мы вычисляем среднюю скорость:

.

В статистической практике чаще используется средняя гармоническая взвешенная, формула которой имеет вид:

. (1.16)

где f_i – вес средней.

Данная формула используется в тех случаях, когда веса (или объемы явлений) по каждому признаку не равны.

Например, необходимо узнать среднюю цену реализованных товаров:

Вид товара	Цена за единицу, рублей	Сумма реализаций, рублей
а б с

Получаем:

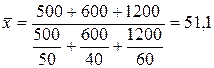(рублей).

Если здесь использовать формулу средней арифметической, то можно получить среднюю цену, которая будет нереальна:

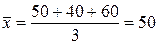(рублей).

Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000). Существуют формулы для простой и взвешенной средней геометрической.

Для простой средней геометрической:

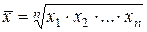. (1.17)

Для взвешенной средней геометрической:

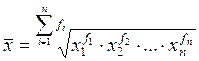. (1.18)

Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения).

Формула простой средней квадратической

. (1.19)

Формула взвешенной средней квадратической

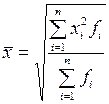. (1.20)

В итоге можно сказать, что от правильного выбора вида средней величины в каждом конкретном случае зависит успешное решение задач статистического исследования. Выбор средней предполагает такую последовательность:

а) установление обобщающего показателя совокупности;

б) определение для данного обобщающего показателя математического соотношения величин;

в) замена индивидуальных значений средними величинами;

г) расчет средней с помощью соответствующего уравнения.

Контрольные вопросы и задания:

1 Дайте определение абсолютной величины.

2 Назовите основные виды относительных величин.

3 Перечислите основные виды средних величин.

4 По какой формуле рассчитывается средняя, если данные несгруппированы:

а) по средней гармонической;

b) по средней арифметической простой;

с) по средней арифметической взвешенной.

5 Задача 1. Имеются данные о стаже работы работников отдела предприятия:

Табельный номер работника
Стаж работы, лет

Определите средний стаж работы.

6 Задача 2. По информации, содержащейся в приведенной таблице, рассчитайте средний размер вклада в банке:

Размер вклада, тыс руб.	Общая сумма вкладов, млн руб.
До 50	43,6
50-100	205,8
100-300	231,6
300-500	274,0
Свыше 500	317,4
Итого	1072,4

Дата добавления: 2014-12-23