Ряды распределения и показатели вариации

Рядом распределения называется упорядоченное распределение единиц совокупности на группы по какому-либо признаку. Виды рядов распределения:

- атрибутивный;

- вариационный;

- дискретный;

- интервальный.

Иными словами, ряд распределения - результат группировки. Под атрибутивным рядом понимается ряд распределения по атрибутивному признаку, не имеющему количественной меры. Например, атрибутивный ряд можно составить по признаку «Возраст», «Профессия», «Пол» и.т.д. (таблица 1.5).

Таблица 1.5 – Группировка студентов по признаку «Возраст»

Возраст, Х лет	Частота	Частость, %
Итого		10,0 55,0 25,0 5,0 5,0 100,0

Частота — количество элементов совокупности, которые имеют данное значение признака.

Частость — отношение частоты к общему количеству исследуемых элементов, т.е. объему совокупности.

Пример дискретного ряда представлен таблицей 1.6.

Таблица 1.6 - Успеваемость в группе студентов-экономистов из 15 человек по одному из предметов

Оценки	Частота	Частость, %
Итого		13,3 26,7 33,3 26,7 100,0

В интервальном ряду значение признака представляется в виде интервалов (таблица 1.7).

Таблица 1.7 - Пример интервального ряда

Заработная плата, тыс. руб.	Частота	Частость, %
5-10 10-20 20-30 30-40 40-50 Итого		100,0

Важно помнить, что в интервальном ряду в качестве основного показателя интервала используется середина интервала.

Для изображения вариационных рядов применяются линейные и плоскостные диаграммы, построенные в прямоугольной системе координат. При дискретной вариации признака графиком вариационного ряда служит полигон распределения (рисунок 1.1.).

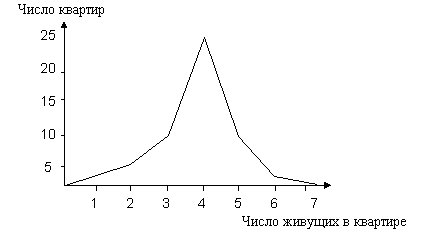
Рисунок 1.1 - Распределение квартир по числу проживающих в них

Полигон распределения представляет собой замкнутый многоугольник, абсциссами вершин которого являются значения варьирующегося признака, а ординатами - соответствующие им частоты.

Кумулята - ломаная кривая, строящаяся на основе прямоугольной системы координат, когда по оси X откладываются значения признака, а по оси Y - накопленные частоты.

Для дискретных рядов на оси откладываются сами значения признака, а для интервальных - середины интервалов.

В случае непрерывного признака строится гистограмма - ступенчатая фигура, состоящая из прямоугольников.

На основе гистограмм можно строить диаграммы накопленных частот с последующим построением интегральной эмпирической функции распределения.

Мода - наиболее типичное, чаще всего встречаемое значение признака. В случаях интервальных рядов с равными интервалами, модальным интервалом считается интервал с наибольшей частотой, а при неравных интервалах - интервал с наибольшей плотностью.

, (1.21)

где x_Mo – нижняя граница модального интервала; i_Mo – величина модального интервала; f_Mo, f_Mo-1, f_Mo+1 – частоты (частости) соответственно модального, домодального и послемодального интервалов.

Таблица 1.8 - Вычисление моды вариационного интервального ряда

Интервал	Частота
70-80 80-90 90-100 100-110 110-120

Mo = 100 + 10 × (45 - 30) / ((45 - 30) + (45 - 13)) = 103,2.

Медиана — значение варьирующего признака, приходящееся на середину ранжированной совокупности. При исчислении медианы интервального ряда сначала находится интервал, содержащий медиану. Медианному интервалу соответствует первый из интервалов, для которых накопленная сумма частот превышает половину общей совокупности наблюдений.

, (1.22)

где x_Me – начало медиального интервала; i_Me – величина медиального интервала; Σ f – сумма частот (частостей) вариационного ряда; f_Me – частота (частость) медиального интервала; S_{Мe- 1} – сумма накопленных частот (частостей) в домедиальном интервале.

Медиана делит вариационный ряд пополам по частотам. Определяют еще квартили, которые делят вариационный ряд на 4 равновеликие по вероятности части, и децили, делящие ряд на 10 равновеликих частей.

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае.

Колеблемость отдельных значений характеризуют показатели вариации. Термин «вариация» произошел от лат. variatio — изменение, колеблемость, различие. Однако не все различия принято называть вариацией.

Под вариацией в статистике понимают такие количественные изменения величины изучаемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают случайную и систематическую вариации. Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов. Например, можно оценить, насколько однородной является совокупность. Для характеристики совокупностей и исчисленных средних величин важно знать, какая вариация изучаемого признака скрывается за средними.

Основа показателей - общая оценка отклонений значений показателей элементов совокупности от средней.

Размах представляет собой разность между максимальной и минимальной величиной признака и является простейшей характеристикой вариации:

R=X_max - X_min. (1.23)

Среднее линейное отклонение:

. (1.24)

Сумма квадратов отклонений от среднего является основой для вычисления относительного показателя — дисперсии в простейшем случае несгруппированных данных:

(1.25)

или дисперсия для сгруппированных данных и для интервальных рядов:

, (1.26)

где .

Корень квадратный из дисперсии называется средним квадратическим отклонением, или стандартным отклонением, и обозначается σ.

Еще одним важным показателем, характеризующим вариацию признака и позволяющим сравнивать вариации различных совокупностей, является коэффициент вариации:

. (1.27)

По величине коэффициента вариации можно судить о степени вариации признаков совокупностей. Чем больше его величина, тем больше разброс значений вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%. Коэффициент вариации важен и в тех случаях, когда нужно сравнивать средние квадратические отклонения, выраженные изначально в разных единицах измерении, для различных совокупностей.

Вопросы для самопроверки:

1 Что такое ряд распределения?

2 Какие вы знаете виды рядов распределения?

3 Что собой представляют средние значения?

4 Какие виды средних вы знаете?

5 Что такое вариация признака?

6 Какими показателями измеряется вариация?

Дата добавления: 2014-12-23