Выборочное наблюдение. Выборочное наблюдение - это такой вид статистического наблюдения, при котором обследованию подвергается не вся изучаемая совокупность

Выборочное наблюдение - это такой вид статистического наблюдения, при котором обследованию подвергается не вся изучаемая совокупность, а лишь часть ее единиц, отобранных в определенном порядке. При этом вся исследуемая совокупность называется генеральной, а единицы, подлежащие наблюдению, составляют выборочную совокупность, или выборку.

Целью выборочного наблюдения является определение параметров генеральной совокупности (генеральной средней - и генеральной доли - р на основе параметров выборочной совокупности выборочной (средней - и выборочной доли - ω). Разница между генеральными и выборочными параметрами называется ошибкой выборки или ошибкой репрезентативности.

Различают два вида отбора повторный и бесповторный. Первый соответствует схеме «возвращенного шара»: после отбора какой-либо единицы она возвращается в генеральную совокупность и снова может быть выбранной. Таким образом, вероятность попадания каждой отдельной единицы в выборку остается постоянной на всем протяжении отбора.

Отбор по схеме «невозвращенного шара» называется бесповторной выборкой. В этом случае отобранная единица не возвращается в генеральную совокупность, и тем самым вероятность попасть в выборку для оставшихся единиц увеличивается с каждым шагом отбора.

При проведении выборочного наблюдения возможны три способа отбора: случайный, отбор единиц по определенной схеме, сочетание первого и второго способов. Различают следующие виды выборочного наблюдения: собственно случайная, механическая, типическая (районированная), серийная (гнездовая), многоступенчатая, многофазная и др.

Одна из задач, решаемая на основе выборочного метода, - определение ошибки выборки. В статистике принято определять среднюю (стандартную), предельную и относительную ошибки выборочного наблюдения.

При случайном и механическом отборах средняя ошибка выборки (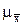) определяется следующим образом:

при повторном отборе:

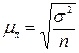, (1.28)

при бесповторном отборе:

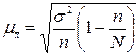. (1.29)

где σ² - дисперсия признака в генеральной совокупности; n - численность выборки; N - численность генеральной совокупности.

Величина (1 - n/N) всегда меньше единицы, поэтому сопоставление приведенных формул свидетельствует о том, что применение бесповторного отбора обеспечивает меньшую ошибку выборки.

На практике величина дисперсии признака в генеральной совокупности (σ ²), как правило, неизвестна, поэтому ее заменяют выборочной дисперсией (S²). Это возможно, поскольку доказано, что соотношение σ ² и S² определяется равенством:

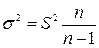. (1.30)

При большой численности выборочной совокупности сомножитель (n/n - 1) стремится к единице и им можно пренебречь.

Величина дисперсии доли в генеральной совокупности определяется по формуле:

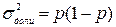, (1.31)

где р - доля единиц, обладающих каким-либо значением признака в генеральной совокупности.

При расчете средней ошибки выборочной доли дисперсия доли в генеральной совокупности, как правило, тоже неизвестна, поэтому ее заменяют дисперсией доли в выборочной совокупности:

, (1.32)

где ω - доля единиц, обладающих каким-либо значением признака в выборочной совокупности.

Формулы для расчета средней ошибки выборочной доли соответственно для повторного и бесповторного отборов имеют вид:

, (1.33)

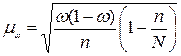. (1.34)

Предельная ошибка выборки (Δ) представляет собой t-кратную среднюю ошибку:

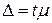, (1.35)

где t - коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной доверительной вероятности.

Приведем наиболее часто употребляемые уровни доверительной вероятности и соответствующие им значения t:

Р(t)	0,683	0,950	0,954	0,990	0,997
t	1,00	1,96	2,00	2,58	3,00

Проявление ошибки большей, чем утроенная средняя ошибка выборки, имеет крайне малую вероятность (1 - 0,997 = 0,003) и считается практически невозможным событием.

Зная величину выборочной средней () или доли (ω), а также предельную ошибку выборки (Δ), можно определить доверительные интервалы, в которых находятся значения генеральных параметров:

(1.36)

Расчет объема выборки по формуле для повторного отбора:

. (1.37)

Если полученный объем выборки превышает 5% численности генеральной совокупности, расчеты корректируют «на бесповторность»:

. (1.38)

Если доля отбора не превышает 5%, к формуле бесповторного отбора можно не переходить, так как это существенно не скажется на величине n.

При решении задачи определения объема выборки величина допустимой предельной ошибки и уровень вероятности, гарантирующей точность оценок будущей выборки, задаются исследователем. Величина генеральной дисперсии, как правило, неизвестна. Для ее оценки можно использовать:

1) выборочную дисперсию по данным прошлых или пробных обследований;

2) дисперсию, найденную из соотношения для среднего квадратического отклонения:

, (1.39)

3) дисперсию, определенную из соотношения для асимметричного распределения:

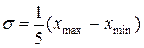, (1.40)

4) дисперсию, вычисленную из соотношения для нормального распределения:

, (1.41)

где - среднее значение признака в генеральной совокупности; х_max, х_min - соответственно максимальное и минимальное значения признака в генеральной совокупности.

В качестве оценки генеральной дисперсии доли используют максимально возможную дисперсию альтернативного признака:

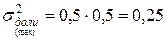. (1.42)

Иногда на практике задается не абсолютная величина предельной ошибки выборки, а ее относительный уровень. Эта величина называется относительной ошибкой выборки:

. (1.43)

Расчет объема выборки при заданном уровне относительной ошибки выборки осуществляется по формулам:

, (1.44)

, (1.45)

где ν - коэффициент вариации, рассчитываемый по формуле (1.27).

Контрольные вопросы и задания:

1 Какой метод наблюдения целесообразно использовать, если изучается работа леспромхозов в регионах, где лесопромышленный комплекс и целлюлозно-бумажная промышленность составляют не менее 5% общего объема производства в регионе?

2 Что такое единица отбора?

3 Решение каких вопросов зависит от объема выборки? Как влияет объем выборки на ее ошибку?

4 Как определить объем выборки, если не известна генеральная дисперсия?

5 По данным прошлых обследований известно, что доля бездетных семей в городе N составляла 5%. Вычислите объем выборки, обеспечивающий относительную ошибку не более 1% с вероятностью 0,954.

Дата добавления: 2014-12-23