Указания по решению задач. Уравнения плоскости и прямой

Уравнения плоскости и прямой

Уравнение плоскости, перпендикулярной вектору 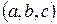и проходящей через точку , в векторной форме имеет вид:

(1.21)

или в компонентах:

. (1.22)

Уравнение прямой, параллельной вектору 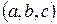и проходящей через точку , имеет вид:

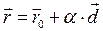, (1.23)

где a ‑ любое вещественное число. Учитывая, что величина a одна и та же для всех координатных осей, получаем, что, уравнение прямой, записанное в компонентах, имеет вид:

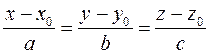. (1.23a)

1.1. Выразить косинус угла между векторам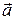и и 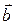через направляющие косинусы этих векторов (направляющие косинусы ‑ косинусы углов между вектором и осями координат).

Указание. Используя определение скалярного произведения (1.7), косинус угла между векторам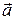и и 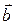, запишем:

= .

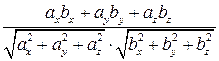Подставляя в полученную формулу выражения (1.12), определяющие значения компонент векторов через их модули и направляющие косинусы с осями координат, получим:

=

= =

= .

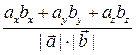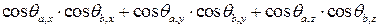Ответ.

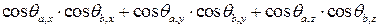
1.2. Дан тетраэдр ABCD, где, например, A(0,1,1), B(1,2,3), C(3,1,0), D(2,1,3). Найти:

1.2.1. Компоненты вектора ;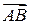

1.2.2. Длину стороны AB;

1.2.3. Угол между векторам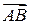и и ;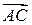

1.2.4. Площадь грани ABC;

1.2.5. Вектор нормали к грани ABC;

1.2.6 Угол между гранями ABC и ABD;

1.2.7. Объем тетраэдра ABCD;

1.2.8. Уравнение плоскости, параллельной плоскости ABC и проходящей через точку D;

1.2.9. Уравнение прямой, параллельной прямой AB и проходящей через точку C.

Указание. К вершинам тетраэдра ABCD проведем из начала координат радиус вектора (0,1,1), (1,2,3), (3,1,0) и т.д.

Вектора 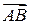, 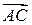и т.д. можно получить из выражений типа:

= ; = .

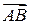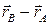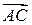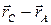Следовательно, 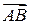(1,1,2) и 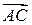(3,0,-1).

= = ; = = .

= = .

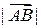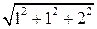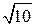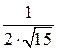Для вычисления площади грани ABC воспользуемся выражением (1.15):

= .

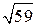Объем пирамиды 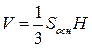, где – площадь основания пирамиды, – высота. Если в качестве основания выбрать грань ABC, т.е. = , то высоту пирамиды можно определить выражением = , а для вычисления объема тетраэдра ABCD получить следующую формулу:

= = = =,

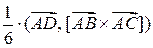где – единичный вектор нормали к грани ABC.

1.3. Найти проекции скорости и ускорения точки, а также угол между скоростью и ускорением в заданный момент времени, если координаты x и y заданы, условиями:

1.3.1. ;

Указание. Для решения предложенных задач следует ввести радиус-вектор , описывающий положение точки в произвольный момент времени t:

= ,

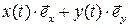найти вектор скорости точки :

= = ,

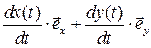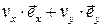а также вектор ускорения точки :

= = .

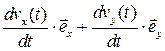В частности, если , а , то:

= ;

= ;

= ;

= .

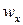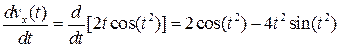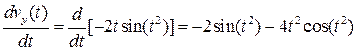Подставив полученные выражения для 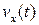, в формулу для , а выражения для и 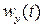в формулу для и положив в полученных выражениях значение t = 1, получим значения векторов скорости и ускорения точки при t = 1.

Угол между скоростью и ускорением в заданный момент времени можно определить, используя определение (1.7) скалярного произведения двух векторов.

1.3.2. ;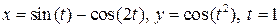

1.3.3. .

1.4. Найти координаты центра масс системы трех частиц с массами m₁, m₂ и m₃, расположенных в точках A₁, A₂ и A₃:

1.4.1. m₁ = 2, m₂ = 4, m₃ = 3, A₁ (0,0,2), A₂ (1,1,0), A₃ (0,1,1);

1.4.2. m₁ = 1, m₂ = 2, m₃ = 2, A₁ (1,0,1), A₂ (0,2,3), A₃ (1,1,1);

1.4.3. m₁ = 3, m₂ = 4, m₃ = 1, A₁ (2,0,0), A₂ (1,2,1), A₃ (-1,1,1);

1.4.4. m₁ = 3, m₂ = 1, m₃ = 2, A₁ (-1,0,1), A₂ (2,3,0), A₃ (1,0,2).

Указание. Для решения задачи введем радиус-вектора , указывающие в ДСК положение частицы с номером , при этом = 1, 2, 3 в соответствии с количеством частиц.

В этом случае радиус-вектор , описывающий в ДСК положение центра масс системы N частиц, определяется следующей формулой [1]:

= .

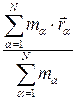Используя это выражение для каждой компоненты , получим значения координат центра масс системы частиц.

1.5. Упростить выражения:

1.5.1. ;

1.5.2. ;

1.5.3. ;

1.5.4. .

1.6. Доказать справедливость тождества:

1.7. Написать уравнение плоскости, проходящей через точку A и перпендикулярной вектору , и уравнение прямой, проходящей через точку A и параллельной вектору :

1.7.1. A(1,2,-3,), (5,7,-6);

1.7.2. A(-2,0,1,), (-1,2,4);

1.7.3. A(1,2,-1,), (0,1,-1).

Указание. Для решения задачи следует воспользоваться выражением (1.22):

,

которое является уравнением плоскости, перпендикулярной вектору 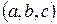и проходящей через точку и выражением (1.23a):

,

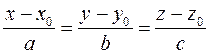которое является уравнением прямой, параллельной вектору 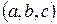и проходящей через точку .

Например, ответы к задаче 1.7.1.

Уравнение плоскости: – ;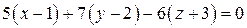

Уравнение прямой: – .

1.8. Найти объем параллелепипеда, построенного на векторах:

.

Дата добавления: 2014-12-27