
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ротор векторного поля и теорема Стокса
|
|
|
|
.
Дивергенция векторного поля и теорема Остроградского-Гаусса
Вектор площадки  направлен перпендикулярно площадке и равен по модулю ее площади. Этот вектор направлен по внешней нормали
направлен перпендикулярно площадке и равен по модулю ее площади. Этот вектор направлен по внешней нормали  , если площадка является элементом замкнутой поверхности, в противном случае считается, что этот вектор связан с направлением обхода площадки правилом правого винта.
, если площадка является элементом замкнутой поверхности, в противном случае считается, что этот вектор связан с направлением обхода площадки правилом правого винта.
Поток DF векторного поля 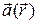 через площадку
через площадку  в точке
в точке 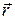 равен
равен
Поток F векторного поля 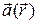 через поверхность S равен сумме потоков этого поля через все площадки
через поверхность S равен сумме потоков этого поля через все площадки  , на которые разбита поверхность S. При
, на которые разбита поверхность S. При  сумма превращается в интеграл по поверхности S:
сумма превращается в интеграл по поверхности S:
 , (3.1)
, (3.1)
где  ‑ средняя точка на площадке
‑ средняя точка на площадке  .
.
В соответствии с определением (3.1) можно определить поток F S векторного поля 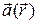 через замкнутую поверхность S:
через замкнутую поверхность S:
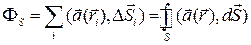 . (3.2)
. (3.2)
Используя понятие стягивающейся к точке 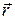 замкнутой поверхности S, ограничивающий некий объем
замкнутой поверхности S, ограничивающий некий объем  , можно ввести определения, независящие от выбора системы координат, следующих величин:
, можно ввести определения, независящие от выбора системы координат, следующих величин:
 ; (3.3)
; (3.3)
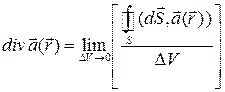 ; (3.4)
; (3.4)
 . (3.5)
. (3.5)
Используя в ДСК в качестве стягивающейся к точке 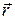 замкнутой поверхности S удобно выбрать поверхность параллелепипеда, длина ребер которого
замкнутой поверхности S удобно выбрать поверхность параллелепипеда, длина ребер которого  , в соответствии с чем и
, в соответствии с чем и  , из данных выше определений легко получить следующие выражения:
, из данных выше определений легко получить следующие выражения:
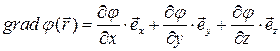 ; (см. (2.2)
; (см. (2.2)
 ; (3.6)
; (3.6)
 =
=  . (3.7)
. (3.7)
С другой стороны поток FS векторного поля  через замкнутую поверхность S может быть записан как сумма потоков
через замкнутую поверхность S может быть записан как сумма потоков  через поверхности дифференциально малых объемов
через поверхности дифференциально малых объемов  , на которые можно разбить замкнутый объем V, ограниченный поверхностью S:
, на которые можно разбить замкнутый объем V, ограниченный поверхностью S: 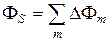 . Чтобы последняя сумма была интегральной (и для нее существовал предел при m ®µ), необходимо, чтобы потоки
. Чтобы последняя сумма была интегральной (и для нее существовал предел при m ®µ), необходимо, чтобы потоки  были пропорциональны соответствующим объемам
были пропорциональны соответствующим объемам 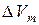 .
.
Как следует из определения (3.4), дивергенция векторного поля 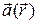 в точке
в точке 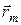 ‑ это скаляр, равный:
‑ это скаляр, равный:  , где
, где 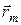 ‑ средняя точка в объеме
‑ средняя точка в объеме 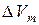 . Отсюда следует, что в пределе при
. Отсюда следует, что в пределе при  сумма по m становится интегралом по объему V:
сумма по m становится интегралом по объему V: 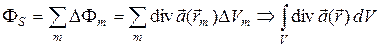 . Представляя этот поток в виде интеграла
. Представляя этот поток в виде интеграла 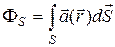 по поверхности S, ограничивающей объем V, мы приходим к теореме Остроградского-Гаусса:
по поверхности S, ограничивающей объем V, мы приходим к теореме Остроградского-Гаусса:
 . (3.8)
. (3.8)
Уравнение непрерывности – дифференциальное уравнение в частных производных, связывающее скорость изменения плотности r жидкости в каждой точке объема и дивергенцию произведения плотности и скорости  жидкости в этой же точке:
жидкости в этой же точке: 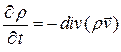 . Уравнение непрерывности выводится из закона сохранения массы с использованием теоремы Гаусса.
. Уравнение непрерывности выводится из закона сохранения массы с использованием теоремы Гаусса.
Закон сохранения электрического заряда в дифференциальной форме ‑ дифференциальное уравнение в частных производных, связывающее скорость изменения плотности электрического заряда r в каждой точке и дивергенцию плотности электрического тока  в этой же точке:
в этой же точке:  . Выводится из закона сохранения заряда с использованием теоремы Гаусса.
. Выводится из закона сохранения заряда с использованием теоремы Гаусса.
Уравнение теплопроводности –дифференциальное уравнение для температуры, которое выводится с использованием теоремы Гаусса из закона сохранения тепловой энергии в процессах теплопередачи. В однородной среде УТ имеет вид:
 ,
,
где a – коэффициент температуропроводности.
Задачи
3.1. Найти:
3.1.1.  ;
;
Указание. Из условия задачи следует, что задано векторное поле 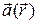 с компонентами:
с компонентами:

Вычислим частные производные:
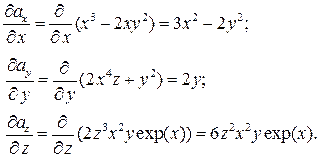
Выражение для дивергенции имеет вид:
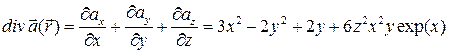 .
.
Ответ:  .
.
3.1.2.  ;
;
3.1.3. 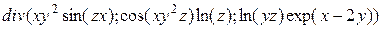 ;
;
3.1.4.  ;
;
3.1.5. 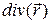 ;
;
Указание. Из условия задачи следует, что векторное поле задано радиус-вектором 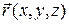 с компонентами x, y, z.
с компонентами x, y, z.
Частные производные:
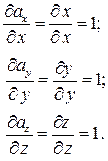
Значение дивергенции  .
.
Ответ:  .
.
3.1.6.  ;
;
Указание. Из условия задачи следует, что векторное поле задано вектором  с компонентами x, y.
с компонентами x, y.
Частные производные:

Значение дивергенции  .
.
Ответ:  .
.
3.1.7.  ;
;
3.1.8. 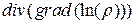 ;
;
3.1.9.  ;
;
3.1.10.  ;
;
3.1.11.  ,где
,где 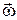 ‑ постоянный вектор;
‑ постоянный вектор;
Указание. Векторное поле задано вектором  с компонентами:
с компонентами:

Частные производные:
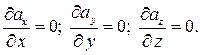
Значение дивергенции 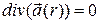 .
.
Ответ: 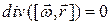 .
.
3.1.12.  , где
, где  и
и 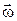 – постоянные вектора;
– постоянные вектора;
Указание. По условию задачи векторное поле задано вектором  .
.
Используя правило раскрытия двойного векторного произведения (1.20), получим:
 .
.
Соответствующие компоненты этого вектора равны:

Частные производные:

Значение дивергенции
 .
.
Ответ:  .
.
3.1.13. 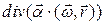 , где
, где  и
и 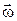 – постоянные вектора;
– постоянные вектора;
3.1.14.  ;
;
3.1.15. 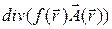 ;
;
3.1.16.  , где
, где  – постоянный вектор;
– постоянный вектор;
3.1.17. 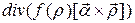 , где
, где  – постоянный вектор;
– постоянный вектор;
3.1.18. 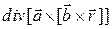 , где
, где 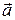 и
и 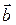 – постоянные вектора;
– постоянные вектора;
3.1.19. 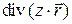 ;
;
3.1.20. 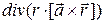 ;
;
3.1.21.  ;
;
3.1.22.  ,
,  ;
;
3.1.23.  , где
, где 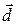 ‑ постоянный вектор.
‑ постоянный вектор.
3.2. Найти поток поля 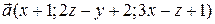 через поверхность
через поверхность 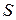 , где поверхность
, где поверхность 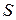 имеет вид:
имеет вид:
3.2.1. 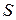 ‑ единичный квадрат, расположенный в плоскости
‑ единичный квадрат, расположенный в плоскости  (стороны квадрата параллельны осям
(стороны квадрата параллельны осям  и
и 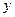 ), положительная нормаль
), положительная нормаль  .
.
Указание. Вектор дифференциально малой площадки по условию задачи  . В соответствии с этим выражение для потока поля
. В соответствии с этим выражение для потока поля  через поверхность
через поверхность 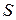 принимает вид:
принимает вид:

Ответ:  .
.
3.2.2. 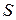 ‑ окружность радиуса
‑ окружность радиуса 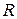 с центром в начале координат, расположенная в плоскости
с центром в начале координат, расположенная в плоскости  , положительная нормаль
, положительная нормаль  .
.
3.2.3. Найти поток поля 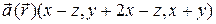 через поверхность сферы радиуса R с центром в начале координат.
через поверхность сферы радиуса R с центром в начале координат.
Указание. Для нахождения потока поля  через поверхность сферы радиуса R воспользуемся теоремой Остроградского-Гаусса (3.8):
через поверхность сферы радиуса R воспользуемся теоремой Остроградского-Гаусса (3.8): 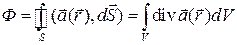 . Для этого найдем вначале выражение для
. Для этого найдем вначале выражение для  :
:
 =
=  .
.
Затем вычислим интеграл по объему сферы:  .
.
Ответ:  .
.
3.3. Проверить теорему Остроградского-Гаусса для единичного кубика, ребра которого параллельны осям x, y, z, и поля  , где
, где  :
:
3.3.1.  ;
;
Указание. Задание проверить теорему Остроградского-Гаусса означает, что необходимо вычислить левую и правую части равенства
 ,
,
являющегося математическим выражением теоремы, и сравнить полученные выражения на предмет их равенства.
Вычислим вначале интеграл по объему:
 =
= 
Затем 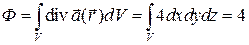 .
.
Интеграл по замкнутой поверхности единичного кубика представим в виде суммы 6 интегралов по его граням. Для этого обозначим грани следующим образом:  и
и  ‑ грани лежащие в координатных плоскостях x=1 и x =0,
‑ грани лежащие в координатных плоскостях x=1 и x =0,  и
и  ‑ грани лежащие в координатных плоскостях y=1 и y=0,
‑ грани лежащие в координатных плоскостях y=1 и y=0,  и
и  ‑ грани лежащие в координатных плоскостях z=1 и z=0. В этом случае вектора дифференциально малых площадок соответственно равны:
‑ грани лежащие в координатных плоскостях z=1 и z=0. В этом случае вектора дифференциально малых площадок соответственно равны:  ;
;  и
и  .
.
Вследствие этого: 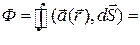
 =
=
=  =4.
=4.
Ответ: Поскольку 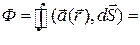 4 и
4 и  , следует, что теорема Остроградского-Гаусса выполняется.
, следует, что теорема Остроградского-Гаусса выполняется.
3.3.2.  .
.
3.4. Проверить теорему Остроградского-Гаусса для единичного кубика, ребра которого параллельны осям x, y, z, и поля  , где
, где  :
:
3.4.1.  ;
;
3.4.2. 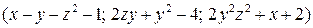 ;
;
3.4.3. 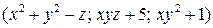 ;
;
3.4.4. 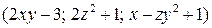 .
.
3.5. Проверить теорему Остроградского-Гаусса для сферы радиуса  с центром в начале координат и поля
с центром в начале координат и поля  , где
, где  :
:
3.5.1.  ;
;
3.5.2. 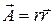 ;
;
3.5.3.  ;
;
3.5.4.  ;
;
3.5.5.  .
.
3.6. Проверить теорему Остроградского-Гаусса для цилиндра с радиусом R и высотой h (ось цилиндра совпадает с осью Oz, нижнее основание лежит в плоскости xOy), и поля  :
:
3.6.1.  ;
;
3.6.2. 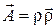 ;
;
3.6.3. 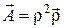 ;
;
3.6.4.  ;
;
3.6.5. 
3.7. Проверить теорему Остроградского-Гаусса для цилиндра с радиусом R и высотой h (ось цилиндра совпадает с осью Oz, нижнее основание лежит в плоскости xOy), и поля  :
:
3.7.1. 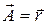 ;
;
3.7.2.  ;
;
3.7.3.  ;
;
3.7.4.  ;
;
3.7.5.  .
.
3.8. Проверить теорему Остроградского-Гаусса для сферы радиуса R с центром в начале координат и поля  :
:
3.8.1.  ;
;
3.8.2.  .
.
3.9. Проверить теорему Остроградского-Гаусса для цилиндра с радиусом R и высотой h (ось цилиндра совпадает с осью Oz, нижнее основание лежит в плоскости xOy), и поля  :
:
3.9.1. 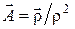 ;
;
3.9.2.  .
.
3.10. Проверить теорему Остроградского-Гаусса для цилиндра с радиусом R и высотой h (ось цилиндра совпадает с осью Oz, нижнее основание лежит в плоскости xOy), и поля  :
:
3.10.1.  ;
;
3.10.2.  .
.
Циркуляция AL векторного поля 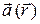 по замкнутому контуру L ‑ скалярная величина, равная сумме скалярных произведений векторов участков
по замкнутому контуру L ‑ скалярная величина, равная сумме скалярных произведений векторов участков  , на которые разбит конур L, и векторов
, на которые разбит конур L, и векторов 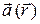 в средних точках этих участков:
в средних точках этих участков: 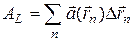 . При
. При 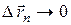 сумма переходит в интеграл по контуру L:
сумма переходит в интеграл по контуру L:
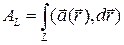 . (4.1)
. (4.1)
Циркуляция меняет знак при изменении направления обхода контура. Циркуляцию по контуру L можно представить в виде суммы циркуляций по границам Lk малых площадок  , на которые разбита поверхность S, натянутая на контур L, причем направление векторов
, на которые разбита поверхность S, натянутая на контур L, причем направление векторов  согласуется правилом правого винта с направлением обхода контуров L и Lk, для которых вычисляются циркуляции:
согласуется правилом правого винта с направлением обхода контуров L и Lk, для которых вычисляются циркуляции:  . Чтобы записанная сумма была интегральной, необходимо, чтобы суммируемые величины были пропорциональны
. Чтобы записанная сумма была интегральной, необходимо, чтобы суммируемые величины были пропорциональны 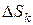 . Это возможно, если существует векторное поле, называемое ротором.
. Это возможно, если существует векторное поле, называемое ротором.  поля
поля 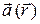 такое, что
такое, что 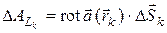 . При
. При  циркуляция записывается в виде интеграла по поверхности S:
циркуляция записывается в виде интеграла по поверхности S: 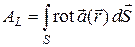 . Таким образом, циркуляция может быть записана как в виде интеграла по контуру, так и в виде потока ротора векторного поля через поверхность, натянутую на контур. Этот результат называется теоремой Стокса:
. Таким образом, циркуляция может быть записана как в виде интеграла по контуру, так и в виде потока ротора векторного поля через поверхность, натянутую на контур. Этот результат называется теоремой Стокса:
 . (4.2)
. (4.2)
Положительное направление нормали для поверхности должно быть связано с направлением обхода контура по правилу правого винта.
Напомним, что ротор векторного поля выражается через частные производные компонент поля соотношением (3.7):
 . (4.3)
. (4.3)
Определитель, стоящий в правой части, надо формально разложить по первой строке, что дает выражение для ротора в виде линейной комбинации единичных ортов (3.7):
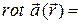
 . (4.4)
. (4.4)
Формула Грина выводится из теоремы Стокса для случая двумерного поля, заданного на плоскости (x, y):  и замкнутого контура L, заданного на плоскости (x, y). Тогда:
и замкнутого контура L, заданного на плоскости (x, y). Тогда: 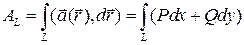 ,
, 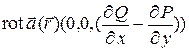 и
и  . Тогда из теоремы Стокса следует формула Грина:
. Тогда из теоремы Стокса следует формула Грина:

 . (4.6)
. (4.6)
Задачи
4.1. Найти:
4.1.1.  ;
;
Указание. Из условия задачи следует, что задано векторное поле 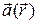 с компонентами:
с компонентами:

Введем вектор  и вычислим его компоненты:
и вычислим его компоненты:

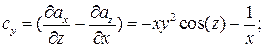

Ответ: Выражение для ротора имеет вид:
 =
= 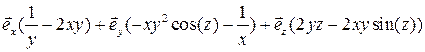 .
.
4.1.2.  ;
;
4.1.3.  ;
;
4.1.4.  ;
;
4.1.5.  ;
;
Указание. Из условия задачи следует, что задано векторное поле 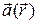 с компонентами:
с компонентами:

Введем вектор 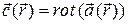 и вычислим его компоненты:
и вычислим его компоненты:
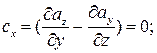
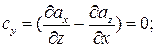

Ответ: Выражение для ротора имеет вид:  , где
, где 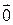 ‑ нулевой вектор.
‑ нулевой вектор.
4.1.6.  ;
;
4.1.7.  ;
;
4.1.8.  ;
;
4.1.9.  , где
, где 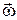 ‑ постоянный вектор;
‑ постоянный вектор;
4.1.10.  , где
, где  и
и 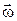 ‑ постоянные вектора;
‑ постоянные вектора;
4.1.11. 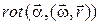 , где
, где  и
и 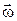 ‑ постоянные вектора;
‑ постоянные вектора;
4.1.12. 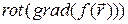 ;
;
4.1.13. 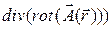 ;
;
4.1.14. 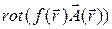 ;
;
4.1.15.  ;
;
4.1.15. 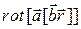 ;
;
4.1.16.  ;
;
4.1.17.  ;
;
4.1.18.  ;
;
4.1.19. 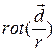 ;
;
4.1.20.  ;
;
4.1.21. 
4.2. Вычислить  ,
,  ,
,  ,
,  ,
,  , где
, где 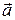 ,
, 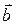 и c равны:
и c равны:
4.2.1.  ,
, 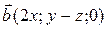 ,
, 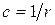 ;
;
4.2.2.  ,
, 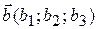 ,
,  ;
;
4.2.3.  ,
,  ,
,  ;
;
4.2.4.  ,
,  ,
, 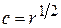 ;
;
4.2.5.  ,
,  ,
, 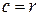 .
.
4.3. Вычислить выражение, где 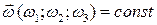 :
:
4.3.1.  ;
;
4.3.2. 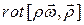 ;
;
4.3.3.  ;
;
4.3.4.  ;
;
4.3.5.  ;
;
4.3.6.  ;
;
4.3.7.  .
.
4.4. Найти циркуляцию поля 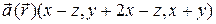 по окружности единичного радиуса с центром в начале координат, лежащей в плоскости
по окружности единичного радиуса с центром в начале координат, лежащей в плоскости
(y, z).
4.5. Проверить теорему Стокса для единичных квадратов в плоскостях  ,
, 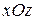 ,
,  и поля
и поля  :
:
4.5.1.  ;
;
Указание. Задание проверить теорему Стокса означает, что следует вычислить левую и правую части равенства, выражающего в математической форме эту теорему:  .
.
Для этого выберем один из предложенных вариантов: единичный квадрат расположен в плоскости  , а векторное поле задано
, а векторное поле задано  .
.
Интеграл по замкнутому контуру представим в виде 4 интегралов по контурам  (координатная линия, определяемая равенствами x=0 и z=0),
(координатная линия, определяемая равенствами x=0 и z=0),  (координатная линия, определяемая равенствами x=0 и y=1),
(координатная линия, определяемая равенствами x=0 и y=1),  (координатная линия, определяемая равенствами x=0 и z =1) и
(координатная линия, определяемая равенствами x=0 и z =1) и 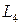 (координатная линия, определяемая равенствами x=0 и y =0). В этом случае соответствующие элементы длины вдоль контуров раны:
(координатная линия, определяемая равенствами x=0 и y =0). В этом случае соответствующие элементы длины вдоль контуров раны:  , а
, а 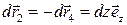 .
.
С учетом сделанных определений
 =
=
 =
= 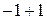 =0
=0
Итак,  .
.
Приступим теперь к вычислению правой части равенства  .
.
Для единичного квадрата, расположенного в плоскости  ,
, 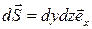 . Следовательно,
. Следовательно, 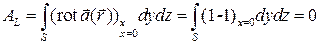 .
.
Ответ: Поскольку  и
и  =0 следует, что теорема Стокса выполняется.
=0 следует, что теорема Стокса выполняется.
4.5.2.  .
.
4.6. Проверить теорему Стокса для граней единичного куба и поля  :
:
4.6.1. 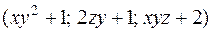 ;
;
4.6.2.  ;
;
4.6.3.  ;
;
4.6.4.  .
.
4.7. Проверить теорему Стокса для окружности радиуса 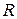 с центром в точке
с центром в точке  , лежащей в плоскости
, лежащей в плоскости  , и поля
, и поля  , где
, где 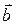 ‑ постоянный вектор.
‑ постоянный вектор.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1914; Нарушение авторских прав?; Мы поможем в написании вашей работы!