Задачи на использование метода оператора набла

Комбинированные задачи векторного анализа

Указание: при решении задач этого параграфа не предлагается использование метода оператора набла.

Задачи

5.1. Вычислить 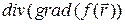для следующих скалярных полей f:

5.1.1. 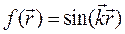, 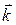‑ постоянный вектор;

Указание. Для решения поставленной задачи вычислим вначале градиент .

Следовательно: ;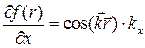

Аналогично: ;

и

Подставляя найденные выражения в (2.2), получим:

Вычислим теперь .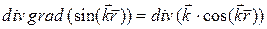

Частные производные: ;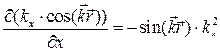

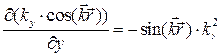
Ответ: .

5.1.2. 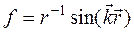, 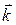‑ постоянный вектор;

5.1.3. 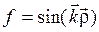, 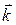‑ постоянный вектор;

5.1.4. 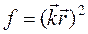, 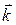‑ постоянный вектор;

5.1.5. , 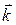‑ постоянный вектор;

5.1.6. ;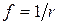

5.1.7. ;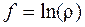

5.1.8. ;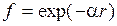

5.1.9. ;

5.1.10. ;

5.1.11. .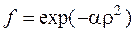

5.2. Вычислить 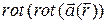для векторных полей :

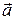5.2.1. ;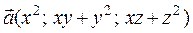

5.2.2. ;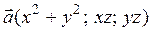

5.2.3. ;

5.2.4. .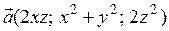

5.3. Вычислить 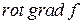для следующих скалярных полей f:

5.3.1. ;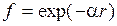

5.3.2. ;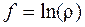

5.3.3. .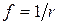

5.4. Вычислить 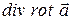для векторных полей :

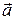5.4.1. 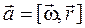, 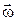‑ постоянный вектор;

5.4.2. .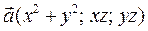

5.5. Упростить выражение с предварительным использованием методов векторной алгебры и вычислить:

5.5.1. ;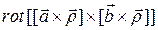

5.5.2. ;

5.5.3. ;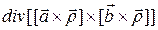

5.5.4. ;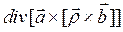

5.5.5. ;

5.5.6. ;

5.5.7. ;

5.5.8. .

Векторный дифференциальный оператор «набла» имеет компоненты 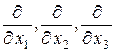и его можно представить в виде: . Алгебраические преобразования выражений, содержащих оператор «набла», проводятся по обычным правилам векторной алгебры, надо только учитывать, что «набла» ‑ это дифференциальный оператор и по определению он должен стоять слева от функции, которую нужно продифференцировать. 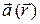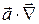Так ‑ это дивергенция поля , а ‑ скалярный дифференциальный оператор: . Понятно, что:

;

;

.

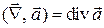Оператор Лапласа ‑ скалярный дифференциальный оператор второго порядка: .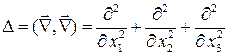

С учетом свойств оператора «набла» легко убедиться, что для любых полей справедливы тождества:

,

,

.

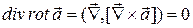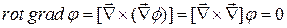Надо иметь в виду, что последний член – это вектор с компонентами .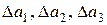

Преобразование выражений векторного анализа методом оператора набла проводится по следующей схеме:

1. Вместо операций grad, div, rot и вводим операции с использованием оператора набла:

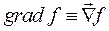
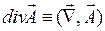
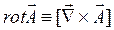
2. Анализируем, на какие функции оператор набла действует как дифференциальный оператор. По определению эти функции должны располагаться в выражении справа от оператора набла. Если таких функций две и они перемножаются, представим оператор набла в виде суммы двух операторов, каждый из которых действует на “свою” функцию. Например:

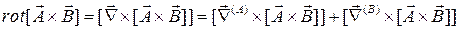
3. Преобразуем полученные выражения, пользуюсь методами векторной алгебры. При этом не обращаем внимания на дифференциальный характер оператора набла и считаем его обычным вектором. В рассматриваемом примере:

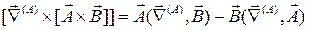
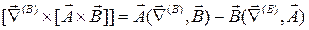
4. Используя стандартные правила векторной алгебры, преобразуем полученные выражения с тем расчетом, чтобы операторы набла стояли слева от тех функций, на которые они действуют, и справа от тех, на которые они не действуют. Так:

=

=

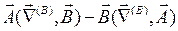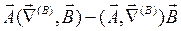
5. Поскольку операторы набла оказываются в позициях, где они автоматически правильно действуют как дифференциальные операторы, убираем пометки у операторов набла и вводим при необходимости обозначения grad, div, rot и . В рассматриваемом примере окончательно получаем:

,

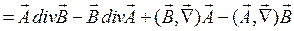где: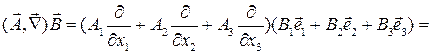

.

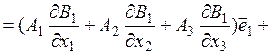
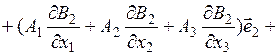
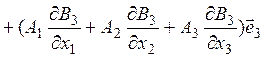Задачи:

6.1. Записать следующие выражения, используя вместо оператора набла операции grad, div, rot и :

6.1.1. ;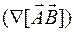

Ответ: .

6.1.2. ;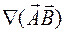

Ответ: .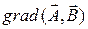

6.1.3. ;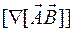

Ответ: .

6.1.4. ;

Ответ: .

6.1.5. ;

6.1.6. ;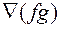

6.1.7. ;

6.1.8. ;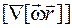

6.1.9. ;

6.1.10. ;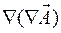

6.1.11. ;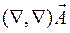

6.1.12. ;

6.1.13. ;

6.1.14. ;

6.1.15. .

6.2. Преобразовать выражение методом оператора набла 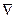и затем расписать в частных производных:

6.2.1. ;

Указание. В соответствии с перечисленными правилами работы с дифференциальным векторным оператором 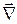необходимо выполнить следующие преобразования:

=

.

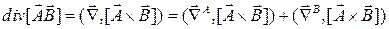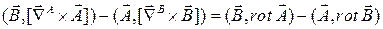Ответ: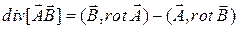

6.2.2. ;

Указание. Рассмотрим вначале выражения для двух других величин:

; (1)

; (2)

Приступим теперь к получению выражения для .

.

С учетом полученных равенств (1) и (2) мы можем провести дальнейшие преобразования:

.

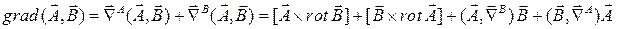Ответ: .

6.2.3. ;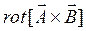

6.2.4. ;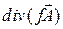

6.2.5. ;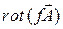

6.2.6. ;

6.2.7. ;

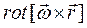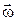6.2.8. , где ‑ постоянный вектор;

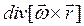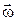6.2.9. , где ‑ постоянный вектор;

6.3. Расписать в частных производных:

6.3.1.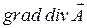

6.3.2. ; ; ;

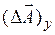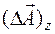6.3.3. ;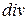

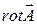6.3.4. ;

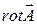6.3.5. ;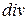

6.3.6. ;

6.3.7. .

6.4. Найти напряженность электрического поля 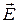, если задан потенциал :

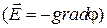6.4.1. ;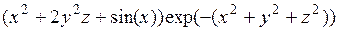

6.4.2. .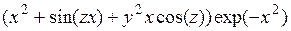

6.5. Найти плотность электрических зарядов в вакууме , если задана напряженность электрического поля :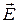

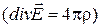6.5.1. ;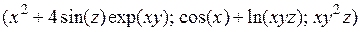

6.5.2. .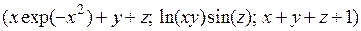

Дата добавления: 2014-12-27