Градиент скалярного поля

Если в каждой точке 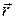пространства задан скаляр 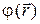– это скалярное поле. Если в каждой точке 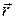пространства задан вектор 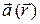– это векторное поле.

Если скалярное поле 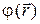задается в ДСК, то это означает, что скалярная функция трех переменных 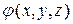. При рассмотрении локального поведения 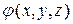часто используется порождаемое им векторное поле , называемое градиентом скалярного поля.

Одно из альтернативных определений этой величины использует понятие производной по направлению, заданному единичным вектором .

Градиентом скалярного поля 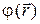в точке 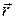называется вектор

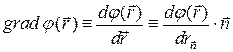, (2.1)

величина которого определяется производной по направлению единичного вектора нормали к поверхности уровня 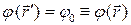, проходящей через точку 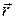, в сторону возрастания значений .

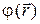Напомним, что нормалью к поверхности S в точке P называется прямая, проходящая через точку P и перпендикулярная к касательной плоскости к S в этой точке.

Компоненты этого вектора в ДСК 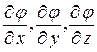можно получить, используя приводимое ранее выражение .

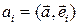Следовательно, в ДСК выражение для градиента скалярного поля 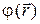имеет вид:

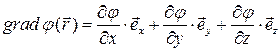(2.2)

Полный дифференциал 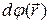от 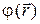определяется как приращение значения этой величины при изменении радиус-вектора 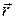на бесконечно малое приращение

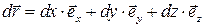(2.3)

Следовательно,

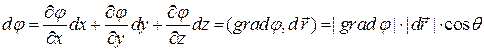, (2.4)

где – угол между векторами градиент и 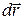. Следовательно, направление вектора – это направление скорейшего роста скалярного поля в данной точке, а модуль градиента – это скорость роста поля в этом направлении.

Экстремальные точки скалярного поля – это точки, при смещении из которых с точностью до членов, линейных по смещению, поле остается неизменным. Из этого определения вытекает, что частные производные 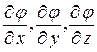в этих точках равны нулю, а возникающую из этого условия систему трех уравнений можно использовать для нахождения экстремальных точек 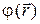. По этой же причине в этих точках .

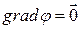Дата добавления: 2014-12-27