Практическое занятие 5

Цель работы: для заданных значений х и у получить зависимость у=f(x) методом корреляционного анализа. Рассчитать коэффициент парной корреляции и коэффициенты корреляционного уравнения. Записать корреляционное уравнение, определить точность прогнозирования у по полученному уравнению. Исходные данные взять из таблицы 2.12.

Таблица 2.12 – Исходные данные для получения корреляционной зависимости

№ вари­анта

Условия задачи

Определить коэффициенты корреляционного уравнения зависимости периода стойкости резцов (Т, мин) от скорости резания (V, м/мин). Материал режущей части резца Т5К10, S=0,6 мм/об. Записать корреляционное уравнение. Определить точность прогнозирования периода стойкости по полученному уравнению  

V(x)
T(y)

Определить коэффициенты корреляционного уравнения зависимости периода стойкости резцов (Т, мин) от толщины пластины (h, мм). Материал резцов Т5К10, режимы резания: V=80 м/мин, t=5,0 мм, S=0,8 мм/об. Определить точность прогнозирования Т(y) по полученному уравнению  

h(x), мм	3,18	4,76	6,35	7,94
T(y), мин	30,30,36	45,50,43	54,60,60	65,65,80

Продолжение таблицы 2.12

Построить график зависимости периода стойкости свёрл (диаметр 6,0 мм, Р6М3) от толщины сердцевины. Определить коэффициенты корреляционного уравнения зависимости периода стойкости Т(мин) от толщины сердцевины d_с (мм). Записать корреляционное уравнение. Определить точность прогнозирования Т по полученному уравнению

dC(x), мм	0,8	1,0	1,1	1,2	1,3
T(y), мин	20,18,22,20	25,30,30,35	35,40,40,45	45,50,55,50	60,55,65,60

Получить степенную корреляционную зависимость разрушающей подачи S_р (мм/об) от толщины пластины (h, мм). Рассчитать коэффициент парной корреляции. Определить точность прогнозирования S_р по корреляционному уравнению

h(x), мм	3,18	4,76	5,50	6,35	7,94
T(y), мин	0,76; 0,92;0,8	1,12; 0,92;1,32	1,53;1,7;1,83	1,83; 2,04;2,04	2,5;3,05;2,65

Получить степенную корреляционную зависимость между разрушающей подачи S_Р периодом стойкости резцов в эксплуатации Т_Э (мин). Резцы: НхВ=25х25 мм; t=0,3 мм; S=0,6 мм/об; V=60 м/мин. Рассчитать коэффициент парной корреляции. Сделать вывод о наличии корреляционной зависимости

Sр(х), мм/об	3,0	2,6	2,2	1,8
Tэ (y), мин	65,75,70	50,55,45	35,45,40	30,25,35

Получить корреляционное уравнение зависимости главной составляющей силы резания Р_z (Н) от глубины резания t(мм). Условия работы: резцы НхВ=25х25 мм; Т5К6; S=0,6 мм/об; V=60 м/мин. Определить точность прогнозирования Р_z по полученному уравнению.

t(x), мм	4,0	4,5	5,0	5,5	6,0
P z(y), H

Получить корреляционное уравнение зависимости периода стойкости свёрл Т(мин) от толщины сердцевины d_с (мм). Свёрла Р6М5, диаметр 6,0 мм. Определить точность прогнозирования Т по полученному уравнению

dс (x), мм	0,76	0,81	1,01	1,06	1,16
T(y), мин	5,10,12,5	15,20,18	22,25,28	30,35,45	60,55,65

Продолжение таблицы 2.12

Построить график зависимости периода стойкости резцов Т_э (мин) от прочности (S_р– разрушающая подача, мм/об). Определить коэффициент парной корреляции между Т_э и S_р. Сделать вывод о тесноте связи.  

Sр(х),мм/об	2,5	1,8	2,4	2,8
Tэ(y), мин	25,40,32,40	22,27,17,15	25,35,30,40	45,60,55,60

Построить график зависимости периода стойкости резцов Т (мин) от угла заострения режущей пластины β (град). Рассчитать коэффициент парной корреляции между Т и β. Сделать вывод о наличии корреляционной зависимости.  

β (х), град
T(y), мин	20,22,18,20	25,30,35,30	35,40,30,42	43,45,50,50

Построить график зависимости периода стойкости метчиков Т(мин) от толщины сердцевины dс (мм). Метчики: Р6М5, М6 0,75. Получить степенную корреляционную зависимость Т от d_с. Рассчитать точность прогнозирования Т по корреляционному уравнению

dс (x), мм	2,0	2,5	3,0	3,5
T(y), мин	15,18,15	18,22,20	24,32,28	30,35,45

Получить степенную корреляционную зависимость прочности твердосплавной пластины (величины разрушающей подачи) S_р (мм/об) и от угла заострения β (град). Рассчитать коэффициент парной корреляции и проверить его значимость. Сделать вывод о наличии корреляционной зависимости

β (х), град
Sр(y), м/об	3,05	2,65	1,83	1,32

Получить степенную корреляционную зависимость периода стойкости резцов Т(мин) от скорости резания V(м/мин). Рассчитать коэффициент парной корреляции и проверить его значимость. Сделать вывод о наличии корреляционной зависимости. Резцы: НхВ=20 20 мм; Т15К6; t=3,0 мм; S=0,4 мм/об  

V(x), м/мин
T(y), мин

Продолжение таблицы 2.12

Получить корреляционное уравнение зависимости периода стойкости спиральных свёрл Т(мин) от толщины сердцевины d_с (мм). Свёрла Р6М5, диаметр 5,0 мм. Построить график зависимости Т от dC. Рассчитать точность прогнозирования периода стойкости по корреляционному уравнению  

d с (x), мм	0,75	0,85	1,05	1,15	1,26
T(y), мин	8,10,12	15,20,19	22,25,28	30,40,35	50,60,55

Получить корреляционное уравнение зависимости периода стойкости резцов Т(мин) от твёрдости (НВ). Материал резцов: Т15К6; режимы резания: t=3,0 мм; S=0,4 мм/об; V=80 м/мин. Рассчитать коэффициент парной корреляции и проверить его значения. Сделать вывод о наличии корреляционной зависимости  

НВ(х)
Т(y), мин

Получить степенную корреляционную зависимость прочности твёрдо сплавных пластин (S_р, мм/об – разрушающая подача)от глубины резания (t, мм). Построить график зависимости SP от t. Рассчитать точность прогнозирования SP по корреляционному уравнению

t(х), мм	4,0	5,0	6,0	8,0
Sр(y), мм/об	3,05	2,65	1,83	1,32

Получить корреляционное уравнение зависимости износа по задней поверхности (hз, мм) от времени работы токарного резца (τ, мин). Рассчитать коэффициент парной корреляции и проверить его значимость. Рассчитать точность прогнозирования h_з по корреляционному уравнению  

τ(x), мин
hз (y), мм	0,18	0,25	0,30	0,32	0,34	0,40

Продолжение таблицы 2.12

Получить степенную зависимость периода стойкости концевых фрез Т(мин) от скорости фрезерования V(м/мин). Обрабатываемый материал – сталь 45. Фреза Р9К10, DФ=30 мм, ширина фрезерования В=20 мм, t=3,0 мм, подача на зуб SZ=0,03 мм/зуб. Построить график зависимости Т от V. Рассчитать точность прогнозирования периода стойкости по корреляционному уравнению  

V(х), м/мин
T(y), мин

Получить корреляционную зависимость периода стойкости спирального сверла Т(количество просверленных отверстий до износа) от скорости резания V(м/мин). Сверло: Р9К10, диаметр 9,8 мм. Обрабатываемый материал – сталь 45, подача S=0,2 мм/об. Рассчитать коэффициент парной корреляции. Сделать вывод о наличии корреляционной зависимости  

V(x), м/мин
Т(y), мм

Получить корреляционную зависимость объёмного износа (Q, мм3) алмазного резца от времени работы (τ, мин). Резец алмазный АС-4, Н В=12 12 мм, обрабатываемый материал – алюминий. Режимы резания: t=0,2 мм, S=0,01 мм/об, V=260 м/мин. Рассчитать коэффициент парной корреляции, сделать вывод о наличии корреляционной зависимости

τ (x), мин
Q(y), мм3

Определить коэффициенты корреляционного уравнения зависимости периода стойкости развёрток (Т, мин) от скорости резания (V, м/мин). Развёртки: Р6М5, диаметр 10 мм, обрабатываемый материал – сталь 45. Режимы резания: t=0,1 мм; S=0,24 мм/об. Записать корреляционное уравнение. Сделать вывод о наличии корреляционной зависимости.

V(x), м/мин
T(y), мин

2.5.1 Содержание и порядок выполнения работы

1 Рассчитывают коэффициент парной корреляции

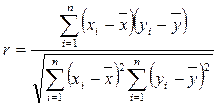, (2.46)

где 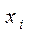- текущие значения ;

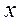- средние значения ;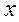

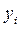- текущие значения ;

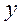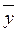- средние значения ;

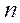- количество исходных данных.

Если для каждого значения 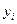дано несколько значений 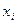, то рассчитывают среднее 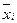для каждого 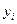,а затем среднее суммарное .

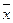Для удобства расчета 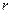результаты сводим в таблицу 2.13.

Таблица 2.13 – Исходные данные для расчета коэффициента корреляции

..
..

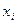
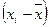
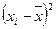
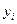
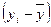
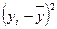
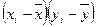
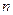
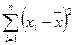
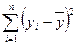
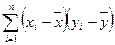
Для получения степенной корреляционной зависимости используют 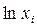и .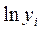

2 Значимость коэффициента корреляции проверяют по критерию Стьюдента

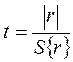, (2.47)

где 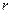- расчетные значения критерия Стьюдента (по абсолютной величине);

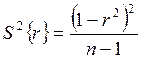. (2.48)

При 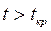, заданной вероятности и числе степеней свободы 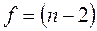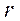считают значимым. Табличные значения 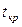приведены в таблице А2 (Приложения А).

3 Корреляционное уравнение записывают в виде

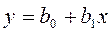, (2.49)

где 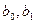- коэффициенты корреляционного уравнения.

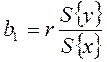, (2.50)

где 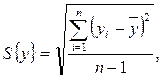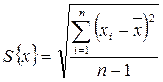. (2.51)

Для расчета и и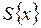спользуют столбцы 4 и 7 таблицы 2.13.

4 Свободный член уравнения (2.49) рассчитывают по формуле

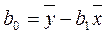. (2.52)

Значения и 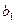записывают в уравнение 2.49. Для получения степенной зависимости результат потенцируют.

5 Для проверки точности прогнозирования 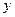по корреляционному уравнению строят в одной системе координат два графика: один – по исходным данным, второй – по результатам расчета 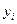по полученному уравнению при заданных значениях 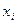. Определяют максимальную ошибку прогнозирования

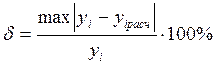, (2.53)

где 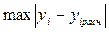- максимальная разность между исходными 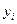и расчетными 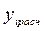значениями .

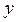2.5.2 Содержание отчета

1 Название и цель работы.

2 Исходные данные для получения корреляционной зависимости.

3 Таблица 2.13 и результаты расчета коэффициентов корреляции.

4 Проверка значимости коэффициентов корреляции.

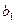5 Результаты расчета коэффициентов и корреляционного уравнения.

6 Результаты оценки точности прогнозирования 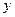по полученному уравнению.

7 Выводы.

2.5.3 Контрольные вопросы

1 Что называют корреляцией?

2 Как определяют коэффициент корреляции?

3 Что характеризует коэффициент корреляции?

4 Как используют коэффициент корреляции для расчета коэффициентов корреляционного уравнения?

5 Как проверяют значимость коэффициента корреляции?

Дата добавления: 2014-12-27