
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример выполнения расчетно-графической работы
|
|
|
|
Рассмотрим расчёт вероятностных эксплуатационных характеристик режущего инструмента и проверку соответствия статистического и теоретического распределения периода стойкости по критерию Пирсона (χ 2), используя для этого значения периода стойкости токарных сборных резцов Н×В=25×25 мм, оснащённых твёрдым сплавом Т5К10.
Расчёт выполняют в следующей последовательности.
1 Располагают данные о периоде стойкости резцов в вариационный ряд (таблица Б.1).
Таблица Б.1 – Вариационный ряд периода стойкости
| Номер испыта-ний i | Период стой-кости 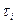 , мин , мин
| Номер испыта-ний i | Период стой-кости 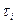 , мин , мин
| Номер испыта-ний i | Период стой-кости
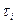 , мин , мин
| Номер испыта-ний i | Период стой-кости 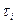 , мин , мин
|
2 Вариационный ряд разбивают на интервалы. Число интервалов рассчитывают по формуле
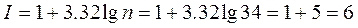 , (Б.1)
, (Б.1)
где n = 34 – количество (объём) исходных данных.
3 Рассчитывают среднее значение периода стойкости
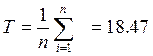 , мин (Б.2)
, мин (Б.2)
4 Рассчитывают среднее квадратичное отклонение периода стойкости
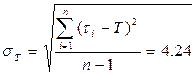 , мин (Б.3)
, мин (Б.3)
5 Рассчитывают коэффициента вариации периода стойкости
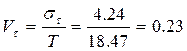 (Б.4)
(Б.4)
6 Исходя из значений коэффициента вариации, принимаем гипотезу о нормальном законе распределения периода стойкости (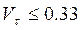 ).
).
7 Для проверки гипотезы о нормальном законе распределения необходимо рассчитать вероятностные эксплуатационные характеристики (показатели надёжности) резцов: плотность распределения 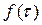 , интенсивность отказов
, интенсивность отказов 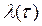 и вероятность безотказной работы
и вероятность безотказной работы 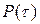 , которую затем используют для расчёта критерия χ2. Значения показателей надёжности рассчитывают для интервалов времени от
, которую затем используют для расчёта критерия χ2. Значения показателей надёжности рассчитывают для интервалов времени от 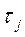 до
до  :
:
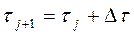 , (Б.5)
, (Б.5)
где 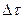 - величина интервала.
- величина интервала.

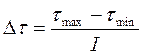 , (Б.6)
, (Б.6)
где  - максимальное и минимальное значение периода стойкости из вариационного ряда;
- максимальное и минимальное значение периода стойкости из вариационного ряда;
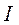 количество интервалов.
количество интервалов.
В нашем случае
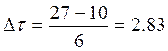 .
.
Для удобства расчётов принимаем 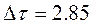 .
.
Данные расчётов удобно свести в таблицу Б.2, которая содержит все необходимые показатели для проверки по критерию χ2.
8 Рассчитывают число отказов 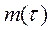 за интервал
за интервал 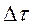 , используя для этого вариационный ряд.
, используя для этого вариационный ряд.
9 Рассчитывают статистические значения 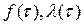 и
и 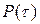 (формулы для расчёта приведены в таблице.2).
(формулы для расчёта приведены в таблице.2).
10 Для каждого интервала рассчитывают теоретические значения 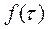 по формуле
по формуле
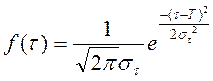 , (Б.7)
, (Б.7)
где - 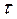 среднее значения периода стойкости для каждого интервала.
среднее значения периода стойкости для каждого интервала.
Результаты расчётов заносят в таблицу Б.2.
11 Для каждого интервала рассчитывают теоретическое значение 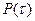 по формуле
по формуле
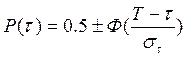 , (Б.8)
, (Б.8)
где 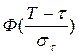 - функция Лапласа. Значения функции Лапласа приведены в таблице 3.5;
- функция Лапласа. Значения функции Лапласа приведены в таблице 3.5;
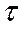 - значение периода стойкости в начале каждого интервала.
- значение периода стойкости в начале каждого интервала.
Результаты расчётов заносят в таблицу Б.2.
12 Для каждого интервала рассчитывают теоретическое значение 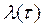 по формуле
по формуле
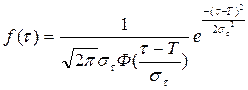 или
или 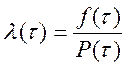 (Б.9)
(Б.9)
Результаты расчётов заносят в таблицу Б.2.
13 Расчёт χ2 выполняют по формулам, приведенным в столбцах 13…17 таблицы Б.2. Сумма значений строк столбца 17 представляет собой значение χ2.
14 Расчётное значение χ2 сравнивают с табличным χ2табл. Расчётное значение χ2 не должно быть больше табличного (χ2≤ χ2табл). Табличные значения χ2 выбирают из таблицы 3.7 при числе степеней свободы  , которое рассчитывают по формуле
, которое рассчитывают по формуле
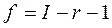 , (Б.10)
, (Б.10)
где 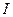 - число интервалов;
- число интервалов;
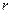 - число параметров закона распределения.
- число параметров закона распределения.
В нашем случае
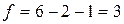
Табличное значение χ2табл = 7,81 при уровне значимости 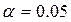 .
.
Таким образом, гипотеза о соответствии статистического и теоретического распределения нормальному закону выбрана правильно (1,94<7,81).
15 По результатам расчётов строят графики 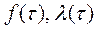 и
и 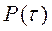 для статистического и теоретического распределений (рис. Б.1…Б.3).
для статистического и теоретического распределений (рис. Б.1…Б.3).
16 При проверке соответствия статистического и теоретического распределения по критерию Колмогорова 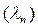 находят максимальное отклонение вероятности безотказной работы для статистического и теоретического распределения
находят максимальное отклонение вероятности безотказной работы для статистического и теоретического распределения
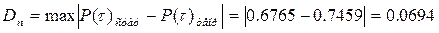 . (Б.11)
. (Б.11)
17 Рассчитывают значение критерия Колмогорова
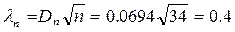 (Б.12)
(Б.12)
По таблице 3.8 для каждого полученного значения 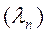 находим
находим 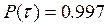 . Это значит, что статистическое и теоретическое распределение согласуются с вероятностью
. Это значит, что статистическое и теоретическое распределение согласуются с вероятностью 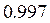 .
.
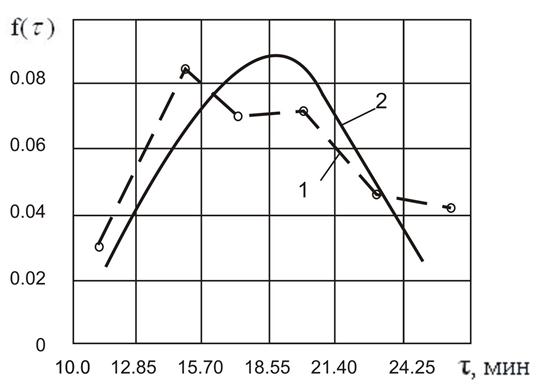
1 – статистическое распределение; 2 – теоретическое распределение
Рисунок Б.1 – Плотность распределения периода стойкости
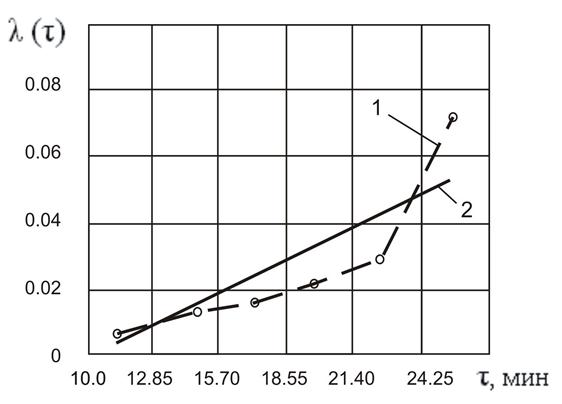
1 – статическое распределение; 2 – теоретическое распределение
Рисунок Б.2 – Интенсивность отказов
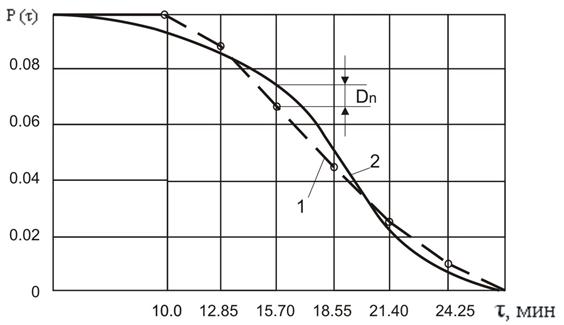
1 – статическое распределение; 2 – теоретическое распределение
Рисунок Б.3 – Вероятность безотказной работы
Таблица Б.2 – Вероятностные эксплуатационные характеристики режущего инструмента.
Проверка статистического и теоретического распределения по критерию Пирсона (χ2)
| Номер интервала j | Граница интервала Δτ =τj+1-τj | Число отказов за интервал Δτ | Число работоспособных инструментов в момент времени τj | Среднее число работоспособных инструментов | Плотность распределения f(τ) | Интенсивность отказов λ(τ) | Вероятность безотказной работы Р(τ) | К проверке соответствия статистического и теоретического распределения по критерию Пирсона | ||||||||
| τj | τj+1 | m(τ) | n(τ) | (nj+nj+1)/2 | Статическая m(τ)/nΔτ | Теоретическая | 2 m(τ)/ (nj+nj+1)Δτ | Теоретическая | n(τ)/n | Теоретическая | ΔP(τ)=P(τj)-P(τj+1) | nΔP(τ) | m(τ)- nΔP(τ) | [m(τ)- nΔP(τ)]2 | [m(τ)- nΔP(τ)]2/ [nΔP(τ)] | |
| 10,00 | 12,85 | 32,5 | 0,0311 | 0,0236 | 0,0326 | 0,0247 | 1,0000 | 1,0000 | 0,0917 | -3,1178 | -0,1178 | 0,0139 | 0,0044 | |||
| 12,85 | 15,70 | 27,0 | 0,0830 | 0,0573 | 0,1040 | 0,0682 | 0,9118 | 0,9083 | 0,1624 | 5,5216 | 2,4784 | 6,1425 | 1,1124 | |||
| 15,70 | 18,55 | 19,5 | 0,0727 | 0,0892 | 0,1267 | 0,1420 | 0,6765 | 0,7459 | 0,2487 | 8,4558 | -1,4558 | 2,1194 | 0,2506 | |||
| 18,55 | 21,40 | 12,5 | 0,0727 | 0,0788 | 0,1967 | 0,2424 | 0,4706 | 0,4972 | 0,2476 | 8,4184 | -1,4181 | 2,0118 | 0,2390 | |||
| 21,40 | 24,25 | 6,5 | 0,0519 | 0,0565 | 0,2715 | 0,3618 | 0,2647 | 0,2496 | 0,1602 | 5,4468 | -0,4468 | 0,1996 | 0,0366 | |||
| 24,25 | 27,10 | 2,0 | 0,0415 | 0,0230 | 0,7059 | 0,4937 | 0,1176 | 0,0894 | 0,0894 | 3,0396 | 0,9604 | 0,9224 | 0,3034 | |||
| Объём данных n=34 | Коэффициент вариации Vτ=0,23 | Число параметров закона распределения r=2 | Критерий χ2= | Σ= 1.9434 | ||||||||||||
| Среднее значение Т=18,47 | Среднее квадратичное отклонение στ=4,24 | Параметры закона: Т=18,47; στ=4,24 | f=j-r-1=3 | |||||||||||||
| Теоретическое распределение - нормальное |
Навчальне посібник
Казакова Тетяна Валентинівна, доц.
Васильева Людмила Володимирівна, доц.
Ковальов Денис Геннадійович, ас.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 331; Нарушение авторских прав?; Мы поможем в написании вашей работы!