Виды физических величин и единиц

Физические величины и их единицы

В науке, технике и обыденной жизни мы имеем дело с разнообразными свойствами окружающих нас тел. Эти свойства отражают процессы взаимодействия тел между собой и их воздействие на органы чувств. Для описания свойств вводятся физические величины, каждая из которых является качественно общей для многих объектов (физических тел, их состояний, процессов, в которых они участвуют), но в количественном отношении различной для разных объектов). Для того чтобы дать меру физической величине, мы устанавливаем единицу. Единица определенной физической величины представляет собой значение данной величины, которое по определению считается равным 1. Операция, с помощью которой мы узнаем числовое значение той или иной величины, представляет собой измерение этой величины. Чтобы измерение физической величины имело однозначный характер, следует обеспечить следующее: отношение двух однородных (одноименных) величин не должно зависеть от того, с помощью какой единицы они измерены. Подавляющее большинство физических величин удовлетворяет этому условию, которое обычно называют условием абсолютного значения относительного количества. Это условие может быть соблюдено при наличии, по крайней мере, принципиальной возможности такого количественного сравнения двух однородных величин, в результате которого получается число, выражающее отношение этих величин.

Но иногда требуется измерить свойства, которые не могут быть охарактеризованы величиной, отвечающей данному требованию. В этом случае вводят некоторые условные величины и соответственно шкалы, рассмотренные выше.

Как видим, существовало и существует большое число разнообразных единиц величин, что создает серьезные трудности, прежде всего, в международных торговых отношениях и обмене результатами научных исследований.

Ранее большинство единиц устанавливалось, как правило, совершенно независимо друг от друга. Исключение в ряде случаев составляли лишь единицы длины, площади и объема. Основные величины выбираются из условия независимости между собой и с учетом возможности установить с их помощью связи с другими физическими величинами. Эти связи устанавливаются с помощью известных закономерностей между основными и производными от них величинами. Таким образом, из нескольких условно выбираемых так называемых основных единиц строятся производные единицы.

В метрологии существуют два вида уравнений, связывающих между собой различные физические величины: уравнения связи между величинами и уравнения связи между числовыми значениями. Первые представляют соотношения между величинами в общем виде, независимо от единиц; вторые могут иметь различный вид, в зависимости от выбранных единиц, входящих в уравнение величин. При этом в уравнениях связи между числовыми значениями часто имеются коэффициенты пропорциональности, именно для установления единиц физических величин используются уравнения связи между числовыми значениями. Первый вид уравнений имеет вид

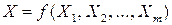, (6)

где 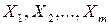– величины, связанные с измеряемой величиной Х некоторым уравнением связи.

Уравнение (6), если 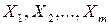представляют основные величины, служат для образования производных величин.

Например, сила F определяется уравнением

,

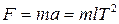где m – масса тела, к которому приложена сила;

a – ускорение, приобретаемое телом при приложении к нему данной силы;

l – длина.

Поскольку длина, масса и время во всех системах представляют основные величины, то сила является производной величиной.

Второй вид уравнений – уравнения связи между числовыми значениями используются для установления единиц измерений. Входящие в уравнение (6) величины можно представить в соответствии с основным уравнением измерений в виде

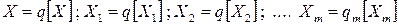, (7)

где 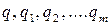– числовые значения;

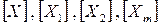– единицы величин.

Дата добавления: 2014-12-27