Определение размерностей

Размерности физических величин

Наличие различных систем ставит задачу перевода одних единиц в другие. Очевидно, изменение основных единиц должно приводить и к изменению производных. Так, например, если вместо метра за единицу пути возьмем километр, то получим единицу скорости километр в секунду, в 1000 раз большую, чем метр в секунду. Взяв в качестве единицы времени час и сохранив в качестве единицы пути метр, получим единицу скорости метр в час, в 3600 раз меньшую, чем метр в секунду. Наконец, можно получить единицу скорости километр в час, равную 1000/3600 м/с ≈ 0,278 м/с, если в качестве единицы длины взять километр, а в качестве единицы времени – час. Мы видим, что всякое изменение основных единиц изменяет соответственно производную единицу.

Желательно найти такое соотношение, которое позволяло бы определить, как с изменением каждой из основных единиц изменится производная единица интересующей нас величины. Такой вопрос впервые поставил в 1822 г. французский математик и физик Ж. Фурье в своей монографии "Аналитическая теория тепла". В этой монографии он ввел понятие и термин "размерность". Согласно этому понятию, если при изменении основной единицы в n раз производная единица изменяется в 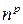раз, то эта производная единица обладает размерностью p по отношению к соответствующей основной единице. Фурье в качестве величин, единицы которых он принял за основные, установил длину, время и температуру. При этом он определил размерности величин, входящих в выведенные им уравнения. Так, для объемной теплоемкости размерность относительно длины оказывается равной "-3", относительно времени – "0" и относительно температуры – "-1".

В СИ и СГС единицы длины, массы и времени являются основными. Поэтому если производная единица величины А изменяется пропорционально степени р изменения единицы длины, пропорционально степени q изменения единицы массы и степени r изменения единицы времени, то единица величины А обладает размерностью р относительно единицы длины, размерностью q относительно единицы массы и размерностью r относительно единицы времени. Символически это записывают в виде

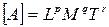, (8)

где квадратные скобки, в которые заключен символ величины А, означают, что речь идет о размерности единицы этой величины относительно единиц длины, массы и времени;

символы L, М и Т представляют собой обобщенные единицы этих величин, без указания конкретного размера единиц[1]). В качестве единицы длины можно принять метр, сантиметр, милю, в качестве единицы массы – килограмм, грамм, тонну, карат, в качестве единицы времени – секунду, час, сутки.

Формулу (8), представляющую собой размерность единицы величины А, называют кратко " размерность А ", подобно тому, как вместо выражения "величина, единица которой принята в качестве основной", применяется сокращенное выражение "основная величина". Термин "размерность физической величины" является распространенным; он узаконен, и мы будем им в дальнейшем пользоваться.

Если в двух системах размерности какой-либо величины совпадают, но размеры основных единиц различны, то отношение производных единиц определится непосредственно размерностью, в которую следует вместо L, М и Т подставить отношения соответствующих основных единиц. Например, если каждую из основных единиц увеличить в 10 раз, то производная единица увеличится в 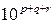раз. Если производная единица не зависит от размера какой-либо из основных единиц, то говорят, что данная производная единица обладает нулевой размерностью по отношению к соответствующей основной единице. Может оказаться, что размер производной единицы не зависит ни от одной из основных единиц. Соответствующую величину называют безразмерной или величиной нулевой размерности по отношению ко всем величинам, принятым за основные.

Размерности могут служить для проверки уравнений, выражающих физические закономерности. Если размерность одной или нескольких величин по отношению хотя бы к одной из основных единиц не совпадает с размерностями других величин, стоящих в уравнении, то можно утверждать, что уравнение ошибочно. Действительно, предположим, что при каком-то выборе размера основных единиц левая и правая части уравнения оказываются численно равными. Пусть при этом размерности левой и правой частей уравнения по отношению к одной из основных единиц не совпадают. Изменим в какое-то число раз размер этой единицы. Очевидно, что левая и правая части уравнения изменятся в разное число раз и прежнее равенство частей нарушится.

Требование равенства размерностей всех членов уравнения, описывающего любое физическое явление, любую физическую закономерность, по существу, совпадает с требованием, чтобы размерность записывалась только для таких величин, для которых удовлетворяется условие абсолютного значения относительных количеств. При этом оказывается, что при любом выборе основных единиц размерность производной единицы представляет собой одночлен, состоящий из произведений размерностей основных единиц в некоторых степенях, причем эти степени могут быть как положительными, так и отрицательными, как целыми, так и дробными.

Докажем это положение, используя для наглядности конкретный пример с определением размерности силы. Пусть два тела одинаковой массы в течение некоторого времени подвержены действию разных сил. Начальные скорости обоих тел равны нулю. В результате тела пройдут разные расстояния, зависящие от действующих сил. Поскольку массы тел и время движения в обоих случаях одинаковы, силы и пройденные расстояния однозначно связаны друг с другом. Будем считать единицу длины основной, т.е. выбираемой произвольно, а единицу силы - производной, т.е. зависящей от выбора единицы длины. Обозначим числовые значения сил F₁ и F₂, а пройденных путей l ₁ и l ₂. Существующие связи между F₁ и l ₁ и между F₂ и l ₂ запишем в общем виде:

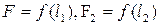. (9)

Из условия абсолютного значения относительных количеств вытекает, что отношение

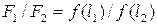(10)

не зависит от выбора единиц. Поэтому единицу длины можно увеличить или уменьшить в любое число раз. Уменьшим эту единицу в x раз.

Соответственно числа, измеряющие пути l ₁ и l ₂, увеличатся в x раз. Таким образом,

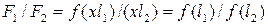. (11)

Перепишем последнее равенство в виде

.

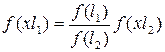Продифференцируем обе части по x:

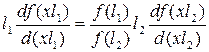. (12)

Так как число x выбрано совершенно произвольно, то (12) должно быть справедливо и при x = 1. В этом случае (12) можно переписать в виде

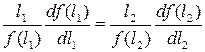. (13)

Это равенство должно выполняться при любых l. Таким образом,

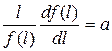, (14)

где a – некоторая постоянная величина.

Разделяя переменные и интегрируя, получим

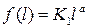. (15)

Если изменить условие задачи и определить числовое значение двух сил, под действием которых два тела разной массы за одно и то же время пройдут одинаковые расстояния, то, повторяя все рассуждения, получим

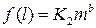. (16)

Подобным же образом для двух тел равной массы, прошедших равные расстояния за разные промежутки времени,

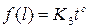. (17)

Общую зависимость можно представить в виде

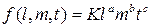. (18)

Коэффициент К представляет собой число, не зависящее от выбора единиц.

Следует ли из полученного результата, что все закономерности, связывающие между собой различные физические величины, могут иметь только степенной характер? Отнюдь нет. Мы ведь знаем, что многие физические законы выражаются тригонометрическими, показательными и другими неалгебраическими функциями. Из соотношения (18) вытекает лишь, что изменение единиц величин, входящих в аргументы соответствующих функций, не должно изменять единиц зависимых величин. Для этого, очевидно, необходимо, чтобы единицы величин, входящих в аргументы неалгебраических функций, образовывали безразмерную комбинацию, т.е. не изменялись при любом изменении единиц, принятых за основные.

Поясним сказанное примером. Пусть конденсатор емкостью С, заряженный до разности потенциалов U, разряжается через сопротивление R. Временная зависимость тока разряда имеет, как известно, экспоненциальный характер:

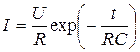. (19)

Для того чтобы равенство (19) сохранялось при любом выборе единиц, необходимо, чтобы показатель степень был безразмерным, а это значит, что произведение RC должно обладать размерностью времени; это произведение получило соответствующее название: "постоянная времени контура". В идеальном колебательном контуре Томсона аналогичная постоянная времени образуется комбинацией .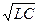

Может возникнуть вопрос: "Как быть в том случае, если установить в рассмотренном примере единицы емкости и сопротивления в качестве независимых, основных единиц?" Очевидно, в этом случае в показатель степени, кроме указанных величин, войдет имеющая размерность постоянная величина. Подобный пример мы имеем в барометрической формуле, выражающей зависимость давления воздуха от высоты. Эту формулу можно представить в виде

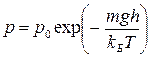, (20)

где h – высота;

m – масса молекулы;

g – ускорение свободного падения;

Т – температура;

k_Б – постоянная Больцмана.

При образовании размерностей производных единиц мы будем пользоваться следующими теоремами.

1) Если числовое значение величины С равно произведению числовых значений величин А и В, то размерность С равна произведению размерностей А и В:

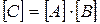(21)

иначе говоря, если

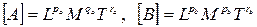. (22)

2) Если числовое значение величины С равно отношению числовых значений величин А и В, то размерность С равна отношению размерностей А и В:

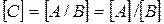, (23)

или

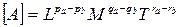. (24)

3) Если числовое значение величины С равно степени n числового значения величины А, то размерность С равна степени n размерности А:

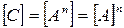. (25)

При

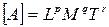
имеем

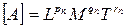. (26)

Доказательства всех этих теорем очень просты, вследствие чего мы ограничимся лишь тем, что докажем первую из них.

Если числовое значение величины С равно произведению числовых значений величин А и В, то это значит, что при измерении этих величин единицами c ₁, a ₁ и b ₁ мы будем иметь

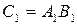, (27)

где

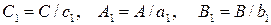. (28)

Соответственно при измерении тех же величин единицами с ₂, a ₂, и b ₂ получим

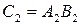, (29)

где

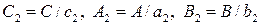. (30)

Беря соотношения (27) и (29) и принимая во внимание (28) и (30), находим

. (31)

Если

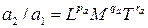, (32)

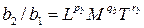, (33)

то

, (34)

что и требовалось доказать. Очевидно, что таким же путем могут быть доказаны и остальные теоремы.

Важно отметить следующее обстоятельство. Так как способ построения производной единицы включает в себя приравнивание единице (или иному произвольному постоянному числу, не зависящему от размера основных единиц) коэффициента пропорциональности в определяющем уравнении, то это означает, что мы условливаемся считать этот коэффициент безразмерным. Поясним сказанное примерами.

1) Размерность площади квадрата можно записать в виде

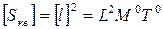(35)

или, опуская здесь, как и в дальнейшем, символы основных единиц, стоящие в нулевой размерности, в виде

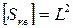. (36)

2) Размерность площади круга будет

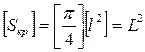, (37)

поскольку коэффициент 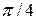является постоянным коэффициентом, не зависящим от размера основных единиц, а потому безразмерным. Поэтому размерность площади любой геометрической фигуры независимо от ее формы будет

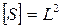. (38)

3) Размерность скорости можно определить из формулы скорости равномерного движения:

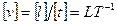. (39)

4) Размерность ускорения определяется из формулы ускорения равноускоренного движения:

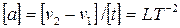. (40)

Для наглядности воспользуемся последней формулой с тем, чтобы определить, как изменится единица ускорения, если от измерения длины в метрах и времени в секундах перейти к измерению длины в километрах и времени в минутах. При таком переходе единица длины увеличивается в 1000 раз, а единица времени – в 60 раз. Согласно формуле (40) единица ускорения изменится в 1000/60² = 10/36 раза, т.е. новая единица ускорения будет равна 0,278 старой.

5) Размерность кинетической энергии, определяемой формулой

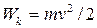, (41)

будет, очевидно, равна (в СИ и СГС)

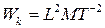. (41 а)

Из последней формулы, в частности, вытекает, что если перейти при измерениях длины от сантиметров к метрам, а при измерении массы от граммов к килограммам и сохранить единицу времени секунду, то единица кинетической энергии увеличивается в (100)²∙1000 = 10⁷ раз.

6) Второй закон Ньютона, записанный в форме

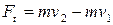, (42)

где 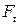– импульс силы,

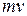– импульс или количество движения тела, определяет размерность силы:

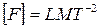. (42 а)

В дальнейшем, исследуя единицы производных величин, мы всегда будем обращаться к размерностям. Размерность производной единицы часто определяет и ее наименование, и ее символическое обозначение. Например, единица скорости метр в секунду обозначается м/с, единица площади квадратный метр – м², и т.д.

Дата добавления: 2014-12-27