Случайные погрешности

Причинами появления случайных погрешностей являются неконтролируемые непрерывные изменения всех факторов (условий), влияющих на результаты измерений и именно такие изменения, воздействие на которые или учет которых всегда бывает возможным только до известных пределов в данном процессе. Поэтому результаты измерений одной и той же величины неизбежно отличаются друг от друга на малые числовые значения. Пределы расхождения результатов измерений, а, следовательно, и случайные погрешности, зависят от точности прибора, опытности наблюдателя, точности учета влияния внешних условий и т. п. Чем точнее прибор, опытнее наблюдатель, чем точнее учитываются внешние условия и т. д., тем меньше будут и случайные погрешности. Но сколь совершенны ни были бы измерения, они не могут быть свободны от случайных погрешностей.

Случайные погрешности нельзя исключить из результата измерений, но их влияние может быть значительно уменьшено путем обработки результатов.

В связи с тем, что возникновение случайных погрешностей неизбежно и неустранимо, основной задачей всякого процесса измерения является доведение погрешностей до минимума. Влияние погрешности может быть значительно уменьшено повышением кратности измерений и вычислением среднего арифметического значения из многократных измерений.

В общем случае вероятность появления случайной погрешности находится в пределах от 0 до 1. Числовое значение какой-либо погрешности нельзя заранее предвидеть, но можно установить вероятность появления каких-либо значений, зная закон распределения случайных погрешностей. Случайные погрешности изучают статистическими методами, в каждом случае рассматривая их совокупности и совершенно не касаясь отдельных погрешностей; роль эксперимента сказывается главным образом при увеличении числа повторных измерений, а также при более тщательном выполнении наблюдений.

Рассматривая случайные погрешности как частный пример случайной величины, можно использовать соответствующий математический аппарат теории вероятностей.

Вероятностной характеристикой дискретной случайной величины является функция ее распределения, показывающая, с какой вероятностью случайная величина принимает те или иные числовые значения.

В отличие от дискретных случайных величин вероятность того, что случайная величина непрерывного типа примет какое-либо определенное значение, равна нулю, так как число возможных значений бесконечно. В качестве вероятностной характеристики случайной величины в этом случае используют понятие плотности вероятностей. Плотность вероятности есть предел отношения вероятности того, что возможные значения величины Х находятся в интервале от X до 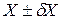к длине интервала 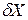, когда 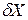стремится к нулю.

Основными числовыми характеристиками результата измерений и его погрешности являются: среднее арифметическое, дисперсия и среднее квадратическое отклонение.

Среднее арифметическое значение Х результата измерений является основной числовой характеристикой центра группирования практического (эмпирического) распределения случайных величин:

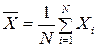. (53)

где 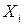– результат измерения величины Q;

N – общее число результатов измерений.

Чтобы различить среднее значение, вычисленное из опытных данных, имеющих ограниченное число наблюдений N, от среднего значения, вычисленного для теоретического распределения, имеющего неограниченное число наблюдений, вводят понятие математического ожидания случайной величины. Для величин дискретного типа

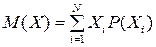(54)

Это значит, что математическим ожиданием случайной величины дискретного типа является сумма произведений всех возможных значений этой величины на вероятности этих значений.

Для случайных величин непрерывного типа с плотностью вероятности f(X) математическим ожиданием будет интеграл

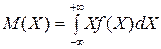. (55)

Основными числовыми характеристиками рассеивания значений случайной погрешности относительно центра группирования являются ее дисперсия и среднее квадратическое отклонение.

Дисперсия D(X) служит мерой рассеивания значений случайной величины Х около центра группирования. Недостатком дисперсии является ее размерность, которая выражается квадратом размерности случайных величин. Поэтому в качестве меры рассеивания значений случайной величины часто применяют среднее квадратическое отклонение :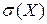

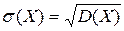. (56)

Среднее квадратическое отклонение имеет ту же размерность, что и случайные величины, мерой рассеивания которых оно является.

Если погрешности результатов измерений ограничиваются интервалами, верхняя и нижняя границы которых с заданной вероятностью включают погрешность результата, то эти границы называются доверительными.

Дата добавления: 2014-12-27