Погрешностей средств измерений

Формы представления погрешностей измерений при установлении классов точности

Классы точности средств измерений

Нормирование метрологических характеристик средств измерений

Метрологические характеристики средств измерений нормируются в государственных стандартах или в технических условиях, содержащих технические требования к средствам измерений. Основные метрологические характеристики – это предел измерений и погрешность измерений. К нормированию погрешностей средств измерений существует два принципиально разных подхода. Первый – отдельно указывают систематическую и случайную составляющие погрешности. Это наиболее полные характеристики, их указывают для эталонов, некоторых особо точных средств измерений специального назначения. В практике подробные характеристики не всегда нужны и поэтому в 90 % случаев используется второй подход к нормированию погрешностей: указывают предельные значения допускаемых погрешностей (предел абсолютной или предел относительной).

Классом точности называется обобщенная характеристика данного типа средств измерений, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.

Для установления классов точности средств измерений во многих странах применяются общие правила, в соответствии с которыми производится количественная оценка гарантированных границ погрешности средств измерений данного типа. В нашей стране такие правила содержатся в ГОСТ 8.401-80 "ГСИ. Классы точности средств измерений. Основные положения". Класс точности не устанавливается на средства измерений, у которых отдельно нормируются систематическая и случайная составляющие основной погрешности, и в тех случаях, когда динамические погрешности являются превалирующими.

Классы точности указываются в стандартах (технических условиях), содержащих конкретные технические требования к тем или иным типам средств измерений. Если средство измерения предназначено для измерений нескольких величин (например, для измерения электрических напряжения и сопротивления), то класс точности определяется для каждой из величин. Так же определяется класс точности для средств измерений, имеющих несколько диапазонов измерений: каждый диапазон имеет свой класс точности.

Присваиваются классы точности средствам измерений при их разработке (по результатам государственных приемочных испытаний). В связи с тем, что в процессе эксплуатации средств измерений их метрологические характеристики обычно ухудшаются, то допускается понижать класс точности по результатам поверки (калибровки) средства измерения.

Форма представления класса точности средства измерений определяется пределами допускаемой основной погрешности измерений. В ряде случаев вместе с основной нормируются пределы допускаемой дополнительной погрешности, форма представления которой может отличаться от формы представления основной погрешности измерений.

Пределы допускаемых погрешностей измерений выражаются границами (верхней и нижней) абсолютной погрешности средства измерений.

Сама форма представления класса точности пределами допускаемой основной абсолютной погрешности применяется преимущественно для мер массы или длины, которые принято выражать в единицах массы или длины. Класс точности измерительных приборов в большинстве случаев выражается пределами допускаемой основной приведенной или относительной погрешности. При этом основой для определения формы представления класса точности прибора является характер изменения основной абсолютной погрешности средства измерении.

1) Если основная абсолютная погрешность имеет аддитивный характер, т.е. границы погрешностей измерительного прибора не изменяются в пределах диапазона измерений (см. рисунок 10, а), то класс точности представляется пределами допускаемой приведенной погрешности:

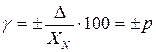, (77)

где γ – приведенная погрешность, %;

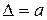– пределы допускаемой основной абсолютной погрешности прибора;

p – отвлеченное положительное число, выбираемое из ряда чисел, указанных ниже;

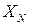– нормирующее значение, выраженное в единицах абсолютной погрешности.

Рисунок 10 – Характерные случаи изменения границ абсолютных

2) Если основная абсолютная погрешность имеет мультипликативный характер, т. е. границы погрешностей измерительного прибора линейно изменяются в пределах диапазона измерений (см. рисунок 10, б), то класс точности представляется пределами допускаемой относительной погрешности 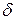в виде

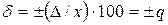, % (78)

где 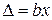– пределы допускаемой основной абсолютной погрешности прибора ;

х – показания прибора (без учета знака измеренной величины);

q – отвлеченное положительное число.

3) Если основная абсолютная погрешность имеет и аддитивную, и мультипликативную составляющие (см. рисунок 10, в), то класс точности представляется пределами допускаемой относительной погрешности 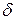в виде

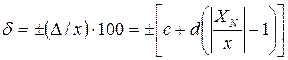, % (79)

где ;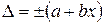

c и d – отвлеченные положительные числа.

Окончательный вид формулы (53) получается путем следующих преобразований:

,

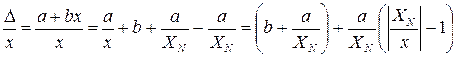причем ; ; отношение 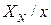берется по модулю с целью учесть наличие двузначных шкал.

Положительные числа р, q, с, d выбираются из установленного ряда:

(n = 1; 0; -1; -2; -3 и т.д.).

На практике редко случается, когда абсолютная погрешность чисто аддитивна или чисто мультипликативна. Поэтому класс точности в виде формулы (77) устанавливается, когда мультипликативной составляющей погрешности можно пренебречь, а в виде (78) – когда несущественна аддитивная составляющая.

Приведем пример. В результате приемочных испытаний вольтметра переменного тока значение основной абсолютной погрешности имеет в зависимости от изменения измеряемой величины чисто мультипликативный характер 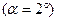. Требуется определить класс точности вольтметра. Очевидно, в данном случае класс точности представляется пределами допускаемой относительной погрешности в виде (78)

,

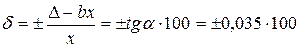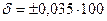
т. е. = ± q * = ± 3,5 % (в пределах диапазона измерений). Однако реальное значение q* = 3,5 не может быть принято для представления класса точности вольтметра. В соответствии с установленным рядом чисел р, q, с, d можно принять ближайшее к числу 3,5 значение q = 4,0, а число п = 0. Отметим, что если бы ближайшим к полученному при испытаниях числу q* было меньшее значение из числа разрешенных, то все равно для установления класса точности пришлось бы воспользоваться большим числом.

Таким образом, класс точности данного прибора устанавливается равным 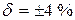. В обиходе говорят, что данный прибор имеет четвертый класс точности.

Дата добавления: 2014-12-27