Обработка результатов измерений с многократными наблюдениями

Обработку группы результатов наблюдений проводят в следующем порядке.

1) Исключают известные систематические погрешности из результатов наблюдений путем введения поправок.

2) Вычисляют среднее арифметическое исправленных результатов наблюдений.

Если во всех результатов наблюдений содержится постоянная систематическая погрешность, допускается исключить ее после вычисления среднего арифметического неисправленных результатов наблюдений.

Среднее арифметическое результатов наблюдений, в которое предварительно введены поправки для исключения известных систематических погрешностей, принимают за результат измерения (2).

3) Вычисляют оценку среднего квадратического отклонения (СКО) результата измерения по формуле

,

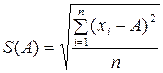где – i -й результат наблюдения;

А – результат измерения (среднее арифметическое исправленных результатов наблюдений);

n – число результатов наблюдений;

S(A) – оценка среднего квадратического отклонения результата измерения.

4) Определяют и исключают грубые погрешности.

В группе результатов наблюдений иногда встречается результат (или несколько), значительно отличающийся от всей группы. Такие анормальные результаты обусловлены наличием так называемых грубых погрешностей. Грубые погрешности – это большие погрешности, вызванные резким изменением условий эксперимента или ошибками оператора.

Анормальные результаты наблюдений, как правило, исключаются из эксперимента. Точно узнать – нормальный или анормальный – нельзя, всегда есть степень риска. Способы определения и исключения грубых погрешностей должны указываться в конкретной методике выполнения измерений.

5) Выполняют доверительные границы случайной погрешности результата измерения.

Рассматриваем случай установления доверительных границ случайной погрешности для результатов наблюдений, принадлежащих нормальному распределению (как наиболее часто встречающийся в измерениях).

Для определения доверительных границ доверительную вероятность принимают равной 0,95: Р = 0,95. В случаях особо ответственных измерений Р =0,99.

Конкретное значение доверительной вероятности указывается в методике выполнения измерений, в зависимости от того, какую степень риска можно считать приемлемой.

Доверительные границы случайной погрешности результата измерения находят по формуле

,

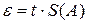где 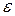– доверительные границы без учета знака;

t – коэффициент Стьюдента, который в зависимости от доверительной вероятности Р и числа результатов наблюдений находят по таблице (приложение 2);

S(A) – оценка среднего квадратического отклонения результата измерения.

6) Вычисляют границы неисключенной систематической погрешности результата измерения. В качестве составляющих неисключенной систематической погрешности рассматриваются погрешности метода, средств измерений и погрешности, вызванные другими источниками.

В качестве границ составляющих неисключенной систематической погрешности можно принять пределы допускаемых погрешностей средств измерений, если случайные составляющие пренебрежимо малы.

Границы неисключенной систематической погрешности вычисляют по формуле

,

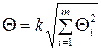где – граница -й неисключенной систематической погрешности;

k – коэффициент, определяемый принятой доверительной вероятностью. при Р = 0,95;

m – число суммируемых погрешностей (обычно ).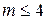

7) Выполняют доверительные границы погрешности результата измерения. Если выполняется условие < S, то систематической погрешностью можно пренебречь и определить доверительные границы погрешности результата, как доверительные границы случайной погрешности (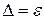). Если > S, то случайной погрешностью по сравнению с систематической можно пренебречь и принять, что граница погрешности результата измерения равна систематической .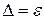

Пример обработки результатов измерений.

С целью калибровки катушки электрического сопротивления при помощи эталона – моста Р 329 проведено 20 наблюдений в следующих условиях: Т=25 °С, давление и влажность в пределах нормы, установленной в нормативных документах на мост и калибруемую катушку. Требуется определить значение сопротивления катушки и погрешность измерений с доверительной вероятностью Р = 0,95 для нормальных температурных условий при Т=20 °С.

В результате измерений получены следующие данные (см. таблицу 6).

Таблица 6

Номера наблюдений	Сопротивление , Ом	Номера наблюдений	Сопротивление , Ом
	1000,4 1001,1 1000,9 1000,6 1000,8 1000,5 1000,0 1000,6 1000,4 1000,5		1000,6 1000,1 1000,6 1000,4 1000,6 1000,5 999,7 1000,3 1000,0 1002,1

Двадцатое наблюдение считаем анормальным, т.е. имеющим грубые погрешности, и исключаем его из дальнейших расчетов.

Вычисляем среднее арифметическое результатов наблюдений

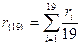
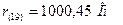
Так как систематическая погрешность обусловлена отклонением условий от нормальных (по температуре), она будет оставаться постоянной для всех наблюдений, поэтому исключаем ее из результата измерений (из среднего значения). Поправку 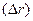, которую надо внести в результат измерения, находим по формуле

,

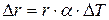где – температурный коэффициент сопротивления материала (ТКС) катушки.

;

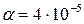тогда .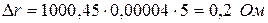

Исправленный результат измерения путем внесения поправки будет таким:

.

Далее вычисляем среднее квадратическое результата измерения

Вычисляем доверительные границы случайной погрешности результата

.

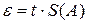По таблице находим коэффициент Стьюдента при доверительной вероятности 0,95 и числе измерений 19: .

.

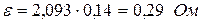Определим доверительные границы для неисключенной систематической погрешности результата измерений.

Неисключенная систематическая погрешность будет обусловлена только одной погрешностью эталона – моста Р 329. Границей этой погрешности считаем предел допускаемой погрешности моста. Мост имеет класс точности 0,05, т.е. предел допускаемой относительной погрешности 0,05%.

Измеренное сопротивление 1000,25 Ом будет сопровождаться неисключенной систематической абсолютной погрешностью

;

;

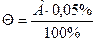Для того чтобы исключить какую-либо из составляющих погрешностей или учесть их обе, найдем соотношение

;

;

< 8;

то систематической составляющей погрешности результата измерения можно пренебречь и принять доверительные границы погрешности результата как доверительные границы случайной погрешности, т.е. .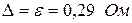

Таким образом, результат измерений должен быть представлен в следующей форме

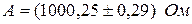при Р = 0,95.

Это значит, действительное значение сопротивления катушки при температуре 20 °С будет находиться в пределах от 999,96 до 1000,54 Ом с доверительной вероятностью 0,95.

Наименьшие разряды числовых значений результатов измерений должны быть такими же, как наименьшие разряды числовых значений среднего квадратического.

Дата добавления: 2014-12-27