Формула Симпсона

Прямі лінії занадто «жорсткі» для наближення кривих. Якщо ми бажаємо мати криву (апроксимувати), проводячи ряд відрізків прямої, потрібно для цієї мети провести велике число малих відрізків. Ми поступимо набагато краще, якщо апроксимуємо криву параболами другого порядку, поєднуючи три послідовні точки. Завжди можна знайти параболу виду

,

Яка проходить через три завдані точки.

Розіб'ємо всю площу на парну кількість смуг, відкладаючи, таким чином, непарну кількість ординат.

Вивід формули для інтегралу не містить нових ідей, у порівняння з виводом формули трапецій, проте є більш громіздким.

Для трьох вузлів формула Симпсона

,

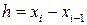
Узагальнена формула Симпсона для рівномірної сітки і парному

Для довільних нерівномірних сіток формули такого вигляду не складають.

Формула Симпсона точна для будь-якого багаточлена другої степені. Але не важко перевірити, що для 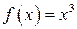ця формула також точна, тобто вона точна для багаточлена третьої степені. Це пояснюється тим, що на рівномірній сітці залишковий член формули трапецій відрізняється тільки по парним степеням кроку.

Похибка формули Симпсона обчислюється аналогічно формулі трапецій. За центр беруть вузол для кожної пари інтервалів 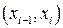і .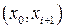

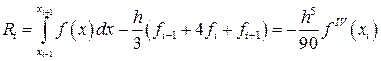
Після додавання попарно сусідніх інтервалів отримаємо

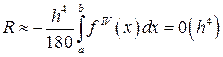
тобто формула Симпсона має четвертий порядок точності, а чисельний коефіцієнт в залишковому члені дуже малий. Ця формула, зазвичай, дає гарну точність при невеликій кількості вузлів (якщо четверта похідна функції не занадто велика).

3. Формула прямокутників (середніх).

Якщо на відрізку взяти єдиний вузол 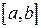квадратної формули 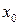, то функція апроксимується константою 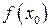. Оскільки симетрія формули чисельного інтегрування призводить до підвищення її точності, то оберемо в якості єдиного вузла середину відрізка . Наближено заміняючи площу криволінійної трапеції площею прямокутника, отримаємо формулу середніх

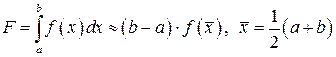
Похибка формули описується стандартно. В даному випадку за центр розкладу потрібно брати середину відрізка, тобто вузол квадратурної формули. Неважко отримати:

Про обчисленні знищується не тільки перший, але й другий член розкладу Тейлора. Це пов'язане з симетричним побудуванням формули середніх, і означає, що формула точна для будь-якої лінійної функції.

Такс само, як і для формули трапецій, для підвищення точності вводиться досить подобна сітка і складається узагальнена формула середніх

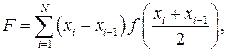
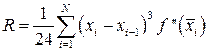
На рівномірній сітці вона має вигляд

.

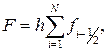
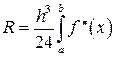Зауваження 1. залишковий член формули середніх приблизно в 62 рази менший, ніж у формули трапецій. Тому, якщо значення функції однакове, легко визначити в будь-яких точках, то краще вести розрахунок по більш точній формулі середніх. Формулу трапецій використовують тоді, коли функція завдана лише в вузлах сітки, а всередині інтервалів невідома.

Зауваження 2. Знаки головного члена похибки в формулі трапецій і середніх відрізняються. Тому, якщо є розрахунки за обома формулами, то точне значення лежить, як правило, у вилці між ними. Ділення цієї величини у відношенні 2:1 дає уточнений результат, відповідний формулі Симпсона.

8. ЧИСЕЛЬНЕ РІШЕННЯ ЗВИЧАЙНИХ ДИФЕРЕНЦІЙНИХ РІВНЯНЬ

Задача Коші.

Потрібно знайти рішення звичайного диференційного рівняння

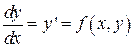(1)

що задовольняє початковій умові .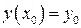

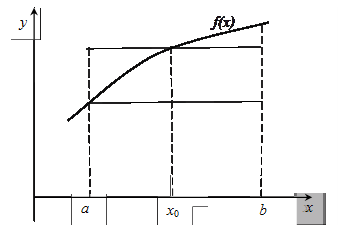
Іншими словами, потрібно знайти криву 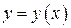, що проходить крізь завдану точку (рис.)

Для диференційного рівняння n -ного порядку

Задача Коші полягає в знаходженні рішення 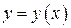, що враховує початкові умови

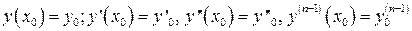
де – завдані числа.

Систему, що містить похідні вищих порядків, і вирішену відносно старших похідних шуканих функцій шляхом введення нових невідомих функцій можна привести до вигляду (5)

Зокрема, для диференційного рівняння n -ного порядку

вважаючи будемо мати еквівалентну систему

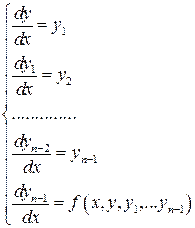
У векторному вигляді

(*)

, , .

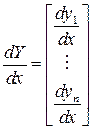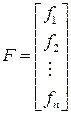Так як система диференційних рівнянь має незліченну можність рішень, то для виділення одного конкретного рішення 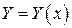, крім рівняння потрібні додаткові умови. У найпростішому випадку завдаються початкові умови

(**)

Що приводить до задачі Коші:

знайти рішення 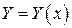системи (*), що задовольняє завданим початковим умовам (**), де 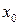– фіксоване значення незалежної змінної і

В доданках часто зустрічаються системи звичайних диференційних рівнянь. Обмежимось розглянутою нормальною системою n -ного порядку звичайних диференційних рівнянь:

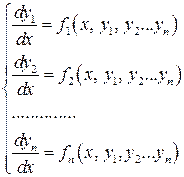
де 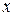– невідома змінна, – шукані функції.

Дата добавления: 2014-12-23