Зауваження. В даному випадку діагональні коефіцієнти 4, 3, 4 системи значно переважають над іншими коефіцієнтами при невідомих

Приклад.

Вирішимо систему

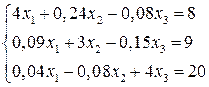
Рішення.

В даному випадку діагональні коефіцієнти 4, 3, 4 системи значно переважають над іншими коефіцієнтами при невідомих. Приведемо цю систему до нормального вигляду

(*)

За нульові наближення коренів приймаємо

Підставляючи ці значення в праві частини рівнянь, отримаємо перші наближення коренів:

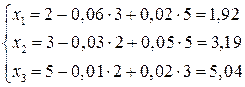
Перевіряємо похибку

Далі, підставляючи ці знайдені наближення в формулу (2) отримаємо друге наближення коренів

.

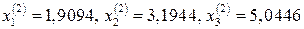Після третьої підстановки будемо мати третє наближення коренів

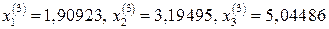і так далі.

1. Інколи вигідно приводити систему (1) до вигляду (2) так, щоб коефіцієнти не були рівня нулю. Наприклад, рівняння

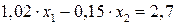
Природно записати у вигляді

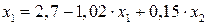
Взагалі маємо систему

Можна вважати

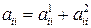
де 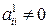. Тоді дана система еквівалентна приведеній системі

,

де при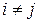

2. Початковий вектор може бути взятий довільно. Немає необхідності за нульові наближення приймати саме стовпчик вільних членів. Збіжність процесу ітерації залежить лише від властивостей матриці α, причому при виконанні відомих умов. Якщо цей процес протікає при будь-якому виборі вихідного начального наближення, то він буде сходитися до того ж граничного вектора і при будь-якому іншому виборі початкового наближення.

Достатні умови збіжності.

Без доказу:

Теорія. Якщо для приведеної системи (2) виконане хоча б одна з умов

1)

чи

2)

То процес ітерації (3) сходиться до єдиного рішення цієї системи, не залежно від обрання початкового наближення.

Наслідки. Для системи

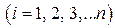
Метод ітерації сходиться, якщо виконуються нерівності

тобто модулі діагональних коефіцієнтів для кожного рівняння системи більше суми модулів усіх інших коефіцієнтів (не враховуючи вільних членів).

Умова є достатньою, але не необхідною. Це означає, що навіть при порушенні її може мат місце збіжність.

Приведення системи до вигляду, зручному для ітерації.

З заданої системи обирають рівняння з коефіцієнтами, модулі яких більше суми модулів інших коефіцієнтів рівняння. Кожне виділене рівняння записують у таку строку нової системи, найбільший за модулем коефіцієнт опинився діагональним.

З залишившихся невикористаних і виділених рівнянь складають лінійно незалежні між собою лінійні комбінації так, щоб виконувався приведений вище принцип комплектування нової системи. При цьому необхідно потурбуватися, щоб кожен невирішене раніше рівняння теж потрапило б в одну лінійну комбінацію.

Наприклад:

В новій системі

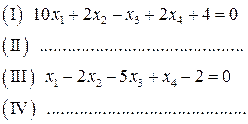
(А) – (Б): 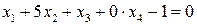буде рівнянням (ІІ).

У нову систему увійшли рівняння (А), (Б) і (Г) тому в рівняння (ІV) обов’язково має увійти рівняння (В).

За рівняння (ІV) можна взяти 2(А) – (Б) + 2(В) – (Г) тобто

Дата добавления: 2014-12-23