Зауваження

Метод Ньютона (дотичних).

Необхідно знайти корінь 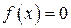на ділянці 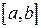, початкове наближення .

1) знаходимо дотичну в точці

оскільки точка задовольняє рівнянню дотичних і 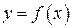, то

Рівняння дотичної

Для наступного наближення :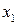

У точці знову проводимо дотичну і так далі

(*)

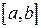Зауваження: якщо обирати , то тобто поза відрізку . Тому початкове наближення 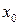повільно задовольняти нерівності

.

Якщо , то метод Ньютона має вигляд

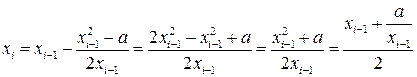
Тому, застосовуючи метод Ньютона, варто керуватися наступним правилом: в якості вихідної точки 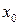обирається той кінець інтервалу , якому відповідає ордината того самого знаку, що і знак .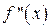

З формули (*) витікає, що чим більше чисельне значення похідної 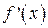в околі даного кореня, тим менше поправка, яку потрібно додати до -ого наближення, щоб отримати і -те наближення.

Тому метод Ньютона особливо зручно застосовувати, коли в околі даного кореня графік функції має більшу крутизну. Проте чисельне значення похідної 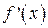коло кореня мале, то поправки будуть великі, і обчислення кореня по цьому методу може виявитись довгим, а інколи і взагалі неможливим. Тобто якщо крива 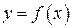коло точки перетину з Ох майже горизонтальна, то використовувати метод Ньютона не рекомендується.

Видозмінений метод Ньютона.

Якщо похідна 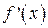мало змінюється на відрізку 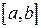, то в формулі (*) можна вважати .

Тоді для кореня ξ рівняння 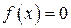отримаємо послідовне наближення

(**)

Геометрично цей спосіб означає, що ми заміняємо дотичну в точці прямими, паралельними дотичній до кривої 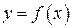, в її фіксовані й точці .

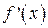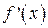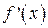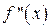По формулі (**) немає необхідності обчислювати кожен раз значення похідної , тому ця функція корисна, якщо складна. Можна довести, що у припущенні сталості знаків похідних і послідовне наближення (**) дають збіжний процес.

Метод хорд (метод пропорційних частин)

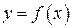Замінимо криву хордою, яка проходить через точки і 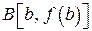. Рівнянням хорди буде

в точці , тоді

(1)

Для доведення збіжності вважатимемо, що корінь відділений і 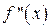зберігає знак на відрізку 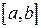. Нехай для визначеності при 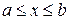(випадок 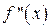зводиться до нашого, якщо записати рівняння в загальному вигляді ).

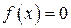Тоді крива буде випукла донизу а, отже розташована нижче хорди А-В. можливі два випадки:

1) 2)

В першому випадку кінець а нерухомий і послідовне наближення при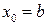

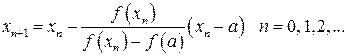(2)

утворюють обмежену монотонно убуваючу послідовність, причому

.

В другому випадку нерухомий кінець b, а послідовне наближення

(3)

Утворюють обмежену монотонно зростаючу послідовність, причому

.

Узагальнюючи результати, заключаємо:

1) нерухомий той кінець, для якого знак функції співпадає зі знаком її другої похідної ;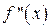

2) послідовне наближення лежить по той бік кореня ξ, де функція має знак, протилежний знаку її другої похідної .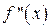

Нехай

(границя існує, так як послідовність обмежена і монотонна).

Переходячи до границі (в рівнянні (2) будемо мати)

.

Так як за припущенням рівняння 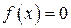має єдиний корінь на 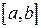, то .

Аналогічно, при переході до границі в (3) доводячи, що для випадку (2).

3. КІНЦЕВІ РІЗНИЦІ. ІНТЕРПОЛЯЦІЯ

Кінцеві різниці різноманітних порядків

Нехай y = f (x) – задана функція. Позначимо через ∆ x = h – фіксовану величину збільшення аргументу (крок). Тоді вираз

∆ y = ∆ f (x) = f (x +∆ x) - f (x) (1)

називається першою кінцевою різницею функції y.

Аналогічно визначаються кінцеві різниці вищих порядків

∆ ⁿy = ∆ ^{n -1}(∆ y) n = 2, 3,…

Наприклад

∆² y = ∆[ f (x + ∆ x) – f (x)] = f (x + 2∆ x) – f (x + ∆ x) – f (x + ∆ x) + f (x) =

= f (x + 2∆ x) – 2 f (x +∆ x) + f (x)

Приклад. Побудувати кінцеві різниці для функції

Р (x) = x ³

уважаючи ∆ x = 1.

∆ Р (x) = (х + 1)³ – х ³ = х ³ + 3 х ²·1 + 3 х ·1³ + 1³ – х ³=3 х ² + 3 х + 1

∆² Р (x) = 3(х + 1)² + 3(х +1) + 1 – 3 х ² – 3 х – 1 =

= 3 х ² + 6 х + 3 + 3 х + 3 + 1 – 3 х ² – 3 х – 1 = 6 х + 6

∆³ Р (x) = 6(х +1) + 6 – 6 х – 6 = 6 х + 6 + 6 – 6 х – 6 = 6

∆⁴ Р (x) = 6 – 6 = 0

∆⁴ Р (x) = 0 при n > 3

Кінцева різниця третього порядку функції Р (x) постійна

Взагалі справедливо стверджування, якщо

Р (x) = а ₀ хⁿ + а ₁ х^{n -1} - а ₂ х^{n -2} +…+ а_n – поліном n -й степені, то

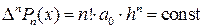
Символ Δ (дельта) можна розглядати як оператор, який ставить у відповідність функції 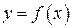функцію (∆ x стале). Легко перевірити основні властивості оператора Δ:

1)

2)

3) ,

де m і n – цілі невід'ємні числа, причому за визначенням

З формули (1) будимо мати

Розглядаючи Δ як символічний множник, отримаємо

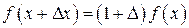
Примінивши це співвідношення n разів, будемо мати

.

Таблиця різниць

Нехай функція 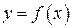задана у вигляді таблиці для системи рівновіддалених точок , і = 0, 1, 2…, де .

Кінцева різниця послідовності 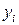визначається відповідностями

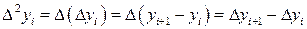
З першого рівняння маємо

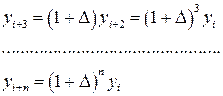
Для подальшого перетворення необхідно звернутися до бінома Ньютона.

Біном Ньютона.

Розклад для цілих додатних n було відомо до Ньютона. Йому належить смілива і досить плідна думка розповсюдити цей розклад і на випадок, коли n від'ємне і дробове.

де

Використовуючи формулу бінома Ньютона, отримаємо

Використовуючи тотожність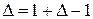

чи

Наприклад:

і так далі,

адже

Зауваження: для обчислення кінцевої різниці потрібно знати n +1 членів даної послідовності.

Кінцеві різниці різноманітних порядків зручно розташувати в формі таблиці двох видів: горизонтальної таблиці різниць чи діагональної таблиці різниць.

Горизонтальна

x	y	Δ y	Δ^2 y	Δ^3 y
x 0	y 0	Δ y 0	Δ^2 y 0	Δ^3 y 0
x 1	y 1	Δ y 1	Δ^2 y 1	Δ^3 y 1
x 2	y 2	Δ y 2	Δ^2 y 2	Δ^3 y 2
……………………………………………………………………………………....

Вертикальна

x	y	Δ y	Δ^2 y	Δ^3 y
х 0	y 0	Δ y 0 Δ y 1 Δ y 2	Δ^2 y 0 Δ^2 y 1	Δ^3 y 0
х 1	y 1
х 2	y 2
х 3	y 3

Приклад. Скласти горизонтальну таблицю різниць функції від початкового значення з кроком .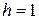

.

x	Y	Δ y	Δ^2 y	Δ^3 y
	-1
……………………………………………………………………………………....

Через те, що наша функція – поліном третьої степені, то третя різниця її стала і рівна:

.

Тому подальше заповнення таблиці можна виконувати з допомогою додавання, використовуючи формули:

Зауваження: Навіть незначна помилка у обчисленнях у значенні функції призводить до значної помилки в її різницях високого порядку.

Узагальнена степінь.

Визначення: узагальненою n -степінню числа х називається добуток n множників, перший з яких дорівнює х, а кожен наступний на h менше попереднього

h – фіксоване стале число.

Вважають .

При узагальнена степінь співпадає зі звичайною. Обчислюють кінцеві значення для узагальненої степені; вважаючи

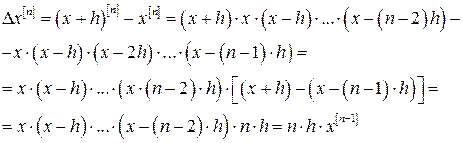
Визначимо другу різницю

Методом математичної індукції легко довести загальну формулу

k = 1, 2, … n.

при k > n.

Перша інтерполяційна формула Ньютона.

Нехай для функції 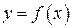задані значення для рівновіддалених значень незалежної змінної і = 0, 1, 2,… n, де h – крок інтерполяції. Потрібно підібрати поліном 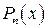степені не вище n, який приймає в точках х значення

(1)

Умови (1) еквівалентні тому, що

при m = 1, 2, … n,

Слідуючи Ньютонові шукати поліном у вигляді

Шукана узагальнена степінь

(*)

Потрібно визначити коефіцієнти .

Вважаючи отримаємо з (*)

Для визначення коефіцієнта 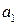складемо першу кінцеву різницю

При

Для визначення складемо кінцеву різність другого порядку

.

При

Послідовно продовжуючи цей процес, можна отримати

, 0! = 1, .

Підставляючи знайдені значення у вираз (*) отримаємо інтерполяційний поліном Ньютона:

(**)

Неважко помітити, що поліном (**) повністю задовольняє вимогам поставленої задачі: степінь його не віще n і .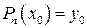

Крім того,

При формула (**) перетворюється у поліном Тейлора для функції у.

Дійсно

Крім того, очевидно

Звідси при формула (**) приймає вигляд полінома Тейлора

Для практичного використання інтерполяційну функцію формулу Ньютона (**) зазвичай записують у певним чином перетвореному вигляді. Для цього введемо нову змінну q, яка визначається формулою

Тоді

=

=

Підставляючи ці вирази у формулу (*) матимемо

(***)

де – кількість членів, необхідних для досягнення точки х ₀. це і є остаточний вигляд першої інтегральної функції Ньютона.

Формулу (***) вигідно використовують для інтерполювання функції 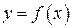в околі початкового значення х ₀, де q мале за абсолютною величиною.

Якщо в формулі (***) вважати n = 1, то отримаємо формулу лінійного інтерполювання

,

при n = 2 будемо мати формулу параболічного чи квадратичного інтерполювання

.

Якщо дана необмежена таблиця значень функції у, то число n в інтерполяційній формулі може бути будь-яким. Практично число n в цьому випадку і обирають так, щоб різниця була сталою із заданою степінню точності. За початкове значення х ₀ можна приймати будь-яке табличне значення аргументу х.

Якщо таблиця значень функції конечна, то число n обмежене: n не може бути більше числа значень функції у, зменшеного на одиницю.

Зауважимо, що при застосуванні першої інтерполяційної формули Ньютона зручно користуватися горизонтальною таблицею різниць, так як тоді потрібні значення різниць функції знаходяться у відповідних горизонтальних строках таблиці.

Приклад. Прийнявши крок h = 0,05, побудувати на відрізку [3,5; 3,6] інтерполяційний поліном Ньютона для функції , заданої таблицею

х	3,50	3,55	3,60	3,65	3,70
у	33,115	34,873	36,598	38,475	40,447

Складемо таблицю різниць:

х	y	Δ y	Δ^2 y	Δ^3 y
3,50	33,115	1,698	0,084	0,005
3,55	34,813	1,785	0,092	0,003
3,60	36,598	1,877	0,095
3,65	38,475	1,972
3,70	40,447

…………………………………………

…………………………………………

Оскільки різниці третього порядку майже сталі, то в формулі вважатимемо n = 3. Прийнявши х ₀ = 3,50, у ₀ = 33,115 будемо мати:

чи

де

Дата добавления: 2014-12-23