
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Похибка частки
|
|
|
|
Похибка добутку.
Відносна похибка добутку декількох наближених чисел, не рівних нулю, не перевищує суми відносних похибок цих чисел.
Нехай 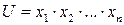 . Нехай для простоти
. Нехай для простоти 
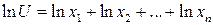
Звідки використовуючи наближену формулу
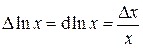
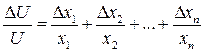
Тоді для відносних похибок
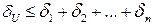
Отже гранична відносна похибка добутку

Граничну абсолютну похибку можна визначити через граничні відносні
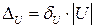 .
.
Якщо  , то
, то 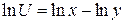
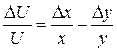
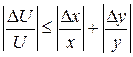
Тобто відносна похибка частки не перевищує суми відносної похибки діленого і дільника. Отже гранична відносна похибка
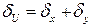
Відносна похибка степені.
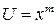
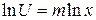
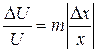

Тобто гранична відносна похибка m -ної степені числа в m разів більша граничної відносної похибки безпосередньо числа.
2. МЕТОДИ РОЗВ'ЯЗАННЯ РІВНЯНЬ ТЕПЛОФІЗИКИ
Наближене рішення алгебраїчних і трансцендентних рівнянь.
Якщо рівняння алгебраїчне чи трансцендентне досить складне, то його корені порівняно рідко вдається знайти точно. Крім того, в деяких випадках рівняння містить коефіцієнти, відомі лише приблизно, і, отже безпосередньо задача щодо точного визначення коренів рівняння втрачає смисл. Тому важливе значення отримують способи наближеного знаходження коренів рівняння і оцінки ступеня їх точності.
Нехай дане рівняння
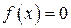 (1)
(1)
де функція  визначена і безперервна у певному кінцевому чи безкінечному інтервалі
визначена і безперервна у певному кінцевому чи безкінечному інтервалі 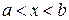 .
.
Будь-яке значення ξ, що обертає функцію  в нуль, тобто
в нуль, тобто  , називається коренем рівняння (1) чи нулем функції.
, називається коренем рівняння (1) чи нулем функції.
Будемо вважати, що рівняння (1) має лише ізольовані корені, тобто, для кожного кореня рівняння (1) існує окіл, який не містить інших коренів цього рівняння.
Наближене знаходження ізольованих дійсних коренів рівняння, зазвичай, складається з двох етапів:
1) визначення коренів, тобто встановлення проміжків  , в яких міститься один і лише один корінь рівняння (1);
, в яких міститься один і лише один корінь рівняння (1);
2) уточнення наближених коренів, тобто доведення їх до завданої точності.
Для визначення коренів корисна відома теорема з математичного аналізу:
|
|
|
|
|
|
|
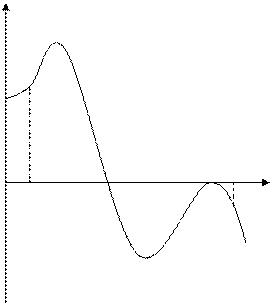 Якщо безперервна функція
Якщо безперервна функція  приймає значення різних знаків н кінцях відрізку
приймає значення різних знаків н кінцях відрізку  , тобто
, тобто 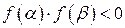 , то всередині цього відрізку міститься хоча б один корінь рівняння
, то всередині цього відрізку міститься хоча б один корінь рівняння 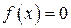 , тобто знайдеться хоча б одне число
, тобто знайдеться хоча б одне число 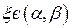 таке, що
таке, що  . (рис. 1).
. (рис. 1).
|
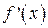 існує і зберігає постійний знак всередині інтервалу
існує і зберігає постійний знак всередині інтервалу  , тобто якщо
, тобто якщо 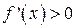 (чи
(чи 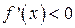 ) при
) при  (рис. 2).
(рис. 2).
 Процес визначення коренів починається з встановлення знаків
Процес визначення коренів починається з встановлення знаків  в граничних точках
в граничних точках 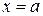 і
і  області її існування.
області її існування.
Потім визначаються знаки функції  в ряді проміжних точок
в ряді проміжних точок 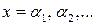 вибір яки враховує особливості функції
вибір яки враховує особливості функції  . Якщо виявиться, що
. Якщо виявиться, що  ,то в силу теореми в інтервалі
,то в силу теореми в інтервалі 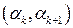 є корінь рівняння
є корінь рівняння 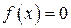 . Потрібно тим чи іншим способом упевнитися, чи є цей корінь єдиним. Для визначення коренів практично часто буває достатньо провести процес половинчастого ділення, наближено ділячи даний інтервал
. Потрібно тим чи іншим способом упевнитися, чи є цей корінь єдиним. Для визначення коренів практично часто буває достатньо провести процес половинчастого ділення, наближено ділячи даний інтервал  на дві, чотири, вісім і так далі рівних частин (до певного кроку), визначаючи знаки функції
на дві, чотири, вісім і так далі рівних частин (до певного кроку), визначаючи знаки функції  в точках ділення. Корисно пам'ятати, що алгебраїчне рівняння n -ної степені
в точках ділення. Корисно пам'ятати, що алгебраїчне рівняння n -ної степені
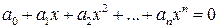 ,
, 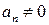
має не більш n дійсних коренів. Тому, якщо для такого рівняння ми отримаємо n + 1 зміну знаків, то всі корені його визначені.
Графічне вирішення рівнянь.
Дійсні корені рівняння
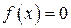 (1)
(1)
Наближено можна визначити, як абсциси точок перетину графіка функції 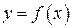 з віссю Ох. Якщо рівняння не має близьких коренів, то цим способом його корені легко визначаються.
з віссю Ох. Якщо рівняння не має близьких коренів, то цим способом його корені легко визначаються.
На практиці часто буває рівняння (1) вигідно замінити рівносильним йому рівнянням (рівняння вважаються рівносильними, якщо вони мають однакові корені)
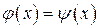 (2)
(2)
де функції 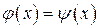 більш прості, ніж функція
більш прості, ніж функція  .
.
Шукані корені отримаємо як абсциси точок перетину цих графіків.
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 2138; Нарушение авторских прав?; Мы поможем в написании вашей работы!