
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм розрахунку
|
|
|
|
Суть алгоритму.
З першого рівняння відома залежність 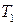 від
від 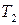 , згідно другого
, згідно другого 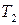 залежить від
залежить від 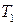 і
і 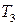 , тобто враховуючи перше рівняння може бути виражене лише через
, тобто враховуючи перше рівняння може бути виражене лише через 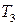 . Виражаючи послідовно
. Виражаючи послідовно  через
через 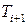 дійдемо до необхідності виразити з останнього рівняння
дійдемо до необхідності виразити з останнього рівняння 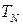 через
через 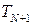 . Проте так як в останньому рівнянні
. Проте так як в останньому рівнянні 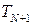 не існує, ми зразу отримаємо чисельне значення
не існує, ми зразу отримаємо чисельне значення 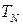 . Після знаходження
. Після знаходження 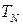 зворотною підстановкою знаходять всі
зворотною підстановкою знаходять всі  через
через 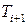 .
.
Докладніше:
З першого рівняння
 , де
, де  (5)
(5)
Підставимо в друге рівняння

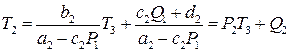 ,
,
де 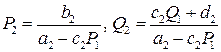 .
.
Аналогічно, підставивши в третє рівняння отримаємо залежність для 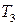 і так далі до
і так далі до 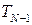 . У загальному вигляді
. У загальному вигляді
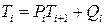 (6)
(6)
де  (7)
(7)

Для останнього рівняння, маючи з передостаннього  отримаємо
отримаємо
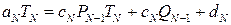
чи
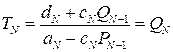 (8)
(8)
Оскільки 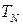 знайдений, то зворотною підстановкою за формулою (6) можна знайти
знайдений, то зворотною підстановкою за формулою (6) можна знайти 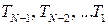
1) обчислюємо  по (5)
по (5)
2) знаходимо 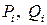 по (7)
по (7)
3) знаходимо 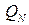 і вважаємо по (8)
і вважаємо по (8)
4) визначаємо  для
для 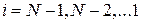 по (6).
по (6).
6. ІТЕРАЦІЙНІ МЕТОДИ РІШЕННЯ СИСТЕМ РІВНЯНЬ
Метод простої ітерації.
Для системи рівнянь
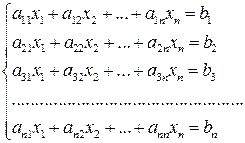 чи у векторному вигляді
чи у векторному вигляді 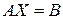 (1)
(1)
Нехай діагональні коефіцієнти 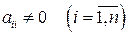 .
.
Вирішимо перше рівняння відносно 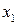 , друге –
, друге – 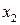 , і так далі. Отримаємо еквівалентну систему.
, і так далі. Отримаємо еквівалентну систему.
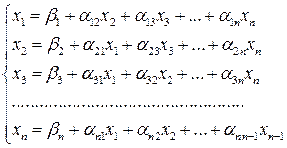 (2)
(2)
де  при
при 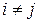 і
і 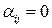 при
при 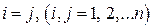 (3)
(3)
Оберемо довільно початкове наближення коренів
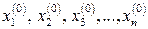 (4)
(4)
намагаючись, звісно, щоб вони певною мірою відповідали шуканим невідомим 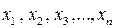 .
.
У якості початкового наближення можна взяти, наприклад, стовпчик відповідних членів
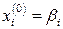 (4').
(4').
Знайдемо перше наближення системи за формулами (2)

чи

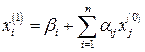 ,
, 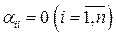
Друге наближення знаходять аналогічно:
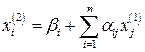 ,
, 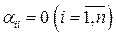
Якщо відомо k -е наближення 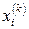 коренів, то (k + 1)-е знаходиться аналогічно
коренів, то (k + 1)-е знаходиться аналогічно
 ,
, 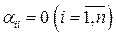 .
.
Якщо послідовність 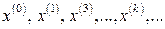 наближень має границю
наближень має границю
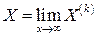
то ця границя є рішенням системи (2).
На практиці розрахунок наближень виконується до тих пір, поки буде виконуватись умова
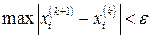
ε – попередньо завдане мале число.
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 489; Нарушение авторских прав?; Мы поможем в написании вашей работы!