Приклад. Метод Гауса-Зейделя (Зейделя)

Метод Гауса-Зейделя (Зейделя).

Метод являє собою певну модифікацію методу інтерполяції. Основна ідея полягає в тому, що при обчислювані (k + 1)-го наближення невідомої враховуються вже обчислені раніше (k + 1)-го наближення невідомі .

Нехай дана приведена система

,

Обираємо довільно початкові наближення коренів

.

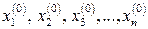Далі, вважаючи, що k-те наближення відомо, будемо будувати (k + 1)-е наближення коренів за формулами

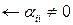
Розрахунки виконуються до тих пір, поки 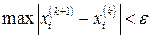, k = 0, 1, 2,…

Зауваження:

1. Теорема збіжності лишається вірною для метода Гауса-Зейделя.

2. Зазвичай метод Гауса-Зейделя дає кращу збіжність, ніж метод простої ітерації.

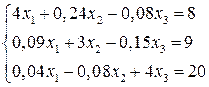
Діагональне переважання.

(*)

Знайдемо похибку на першій стадії

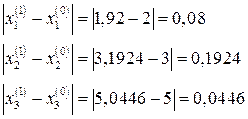
Нехай похибка дорівнює .

Тоді , тому знову підставляємо в (*) і отримаємо і так доти, док не виконається умова .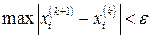

7. МЕТОДИ ОБЧИСЛЕННЯ ІНТЕГРАЛІВ

1. Формула трапецій.

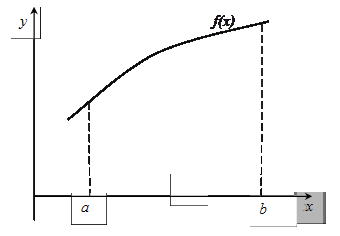Нехай необхідно знайти визначений інтеграл . Замінимо на відрізку криву на січну. Шуканий інтеграл,рівний площі криволінійної фігури, заміняється на площу трапеції. З геометричних міркувань неважко написати для нього функції трапецій

(1)

Це одна з найпростіших квадратних формул. Знайдемо її похибку. Для цього розкладемо за формулою Тейлора, обираючи середину відрізку за центр розкладу, і вважаючи у функції є потрібні по ходу розмірковувань безперервні похідні:

(2)

Похибкою є різність точного і наближеного значень інтеграла. Підставляючи в (1) розклад (2), отримаємо головний член похибки

(3)

Де члени, отримані при заміні точної рівності наближеним, містять старші похідні і більш високі ступеня довжини відрізку інтегрування.

Взагалі кажучи, довжина відрізку (b – a) не мала, тому залишковий член (3) може бути великим. Для підвищення точності на відрізку 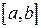вводять досить густу сітку . Інтеграл розбивають на суму інтегралів по кроках сітки і до кожного кроку застосовують формулу (1). Отримують узагальнену формулу трапеції.

(4)

На рівномірній сітці вона спрощується

.

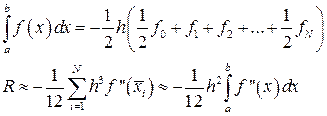
Таким чином, узагальнена функція трапеції має другий порядок точності відносно кроку сітки.

Такий шлях дає точне значення для лінійних функцій.

Дата добавления: 2014-12-23