Двойственность

Определение.Функция называется двойственной к функции 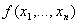, если 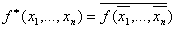; функция, двойственная к самой себе, называется самодвойственной, т.е. .

Отношение двойственности симметрично, т.е., если 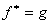, то . Пример 2.2.6 - Дизъюнкция двойственна конъюнкции, конъюнкция –

дизъюнкции, константа 1 – константе 0 и константа 0 – константе 1, отрицание самодвойственно. Действительно, например, для 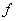= имеем ; для 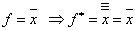, т.е. .

Двойственную функцию можно получить также с помощью таблиц истинности, заменяя в таблице истинности функции 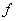все значения на противоположные.

Пример 2.2.7 - Для функции 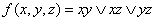получим двойственную функцию двумя способами:

I способ. , т.е. .

II способ. Построим таблицу истинности для 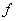(см. таблицу 2.2.7), затем заменим в ней все значения на противоположные, получим таблицу для (см. таблицу 2.2.8). По таблицам видно, что эта функция самодвойственна . Заметим, что для получения таблицы функции в обычном виде, где значения переменных расположены в лексикографическом порядке, нужно все столбцы последней таблицы «перевернуть».

Т а б л и ц а 2.2.7 Т а б л и ц а 2.2.8

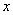
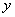
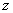
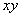
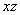
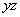
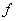
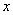
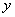
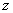
Принцип двойственности:если в формуле , представляющей функцию 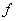, все знаки функций заменить на знаки двойственных функций, то полученная формула будет представлять функцию двойственную функции 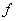. В булевой алгебре принцип двойственности имеет более конкретный вид, вытекающий из выше приведенного примера: если в формуле , представляющей функцию 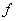, все конъюнкции заменить на дизъюнкции, дизъюнкции на конъюнкции, 1 на 0, 0 на 1, то получим формулу , представляющую двойственную функцию .

Классы Поста. Полные системы логических функций

Пусть дана булева функция 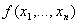. Введём определение классов булевых функций или классов Поста:

а) говорят, что функция 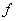сохраняет константу 0, если .

Множество всех функций, сохраняющих 0, образует класс ( );

б) говорят, что функция 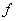сохраняет константу 1, если .

Множество всех функций, сохраняющих 1, образует класс ( );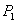

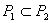в) обозначим через 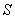множество или класс самодвойственных

функций;

г) функция 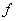называется линейной, если она может быть записана в

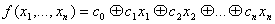виде , где 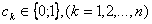. Класс линейных функций обозначается ;

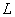д) функция 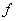называется монотонной, если для любых наборов нулей и

единиц и из условий 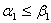,…, следует 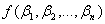. Обозначим через 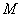класс монотонных функций.

Каждый класс Поста замкнут относительно операций замены переменных и суперпозиции, т.е. с помощью этих операций из функций данного класса можно получить только функции этого же класса.

В таблице ниже рассмотрены примеры принадлежности некоторых булевых функций к классам Поста (принадлежит – (+); не принадлежит – (-)).

Т а б л и ц а 2.2.9

Функция
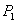
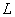
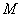
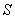
Отрицание	-	-	+	-	+
Конъюнкция	+	+	-	+	-
Дизъюнкция	+	+	-	+	-
Импликация	-	+	-	-	-

Одна и та же логическая функция может быть задана формулами,

включающими различные наборы логических операций. Например, 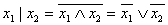. Существуют наборы логических операций (функций), через которые можно выразить любые другие логические функции.

Определение.Системалогических функций 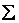называется функционально полной системой или базисом, если любая логическая функция является суперпозицией функций из .

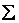Ответ на вопрос о полноте произвольной системы функций даёт следующая теорема.

Теорема Поста. Для того чтобы система булевых функций была полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию, не сохраняющую 0, хотя бы одну функцию, не сохраняющую 1, хотя бы одну не самодвойственную функцию, хотя бы одну нелинейную и хотя бы одну не монотонную функции.

При определении полноты булевых функций можно пользоваться таблицами принадлежности этих функций классам Поста. Например, так как в системе 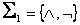отрицание не сохраняет констант и не монотонно, а конъюнкция не линейна и не самодвойственна (см. таблицу 2.2.9), то эта система полна. Примерами функционально полных систем являются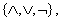 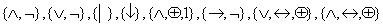и другие. Формулы, содержащие, кроме переменных и скобок, только операции конъюнкции, дизъюнкции и отрицания, называются булевыми.

Теорема.Всякая логическая функцияможет быть представлена булевой формулой (т.е. как суперпозиция конъюнкции, дизъюнкции и отрицания).

Отсюда следует, что системa 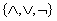функционально полна. Для доказательства функциональной полноты какого-либо другого набора операций, кроме указанного выше способа, достаточно показать, что через операции набора можно выразить конъюнкцию, дизъюнкцию и отрицание. Справедливо и более общее утверждение, позволяющее доказать полноту системы другим способом.

Теорема.Если все функции функционально полной системы представимы формулами над 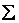, то 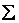также функционально полна.

Пример 2.2.8 -Рассмотрим системы 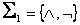и и базис 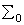= 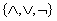. Докажем, что 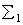, также базисы. Действительно, в каждой из этих систем недостающая до 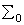операция может быть выражена через остальные две: для 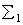не достаёт « »:

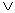для не достаёт « »: ( ).

Формула в системах 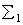, перейдёт соответственно в формулы: =[ ] , [ ] .

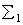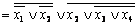Таким образом, с точки зрения функциональной полноты систему 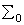можно считать избыточной, т.к. она сохраняет свойство полноты и при удалении из неё дизъюнкции или конъюнкции. Но, как мы видим, за не избыточность систем 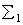, приходится платить избыточностью формул, т.к. каждая замена одной операции на другую по формулам ( 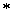) вносит в формулу лишнее отрицание.

Дата добавления: 2014-12-27