
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Функции алгебры логики
|
|
|
|
Каждая формула представляет логическую функцию от логических переменных, которые могут принимать только два значения 0 и 1.
Определение.Функцией алгебры логики ( логической функцией ) от nпеременных 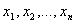 ( обозначается
( обозначается 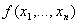 ) называется любая функция, которая произвольному набору
) называется любая функция, которая произвольному набору 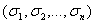 нулей и единиц ставит в соответствие значение
нулей и единиц ставит в соответствие значение  , т.е.
, т.е. 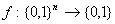 .
.
Функции алгебры логики называются также булевыми, двоичными или переключательными(обозначаются в некоторых учебниках  ).
).
Эти функции описывают преобразование некоторым устройством входных сигналов в выходные. Пусть устройство имеет n входов 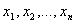 , на которыеможет подаваться или не подаваться ток, и один выход, на который ток подаётся или не подаётся, в зависимости от подачи тока на входы (см. рисунок 2.2.1).
, на которыеможет подаваться или не подаваться ток, и один выход, на который ток подаётся или не подаётся, в зависимости от подачи тока на входы (см. рисунок 2.2.1).

| ||||||||||
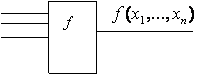
| ||||||||||
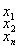
| ||||||||||
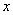
| ||||||||||

| ||||||||||
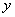
| ||||||||||
Рисунок 2.2.1 Рисунок 2.2.2
Значение 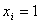 понимается как поступление тока на i-ый вход;
понимается как поступление тока на i-ый вход;  - как не поступление. Значение
- как не поступление. Значение  (где
(где  ), если ток на выходе проходит и
), если ток на выходе проходит и  - если не проходит.
- если не проходит.
Так, например, функции  , представляющей операцию конъюнкции, соответствует устройство с двумя входами и одним выходом (см. рисунок 2.2.2). При этом значение выхода равно 1 тогда и только тогда, когда оба значения входов равно 1.
, представляющей операцию конъюнкции, соответствует устройство с двумя входами и одним выходом (см. рисунок 2.2.2). При этом значение выхода равно 1 тогда и только тогда, когда оба значения входов равно 1.
Способы задания логических функций
Наиболее распространённые способы задания функций следующие:
а) задание таблицей истинности, в левой части которой выписаны все возможные наборы значений аргументов 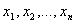 , а в правой – столбец значений
, а в правой – столбец значений 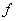 , соответствующих этим наборам. Число всех наборов 0 и 1 функции n переменных будет равно
, соответствующих этим наборам. Число всех наборов 0 и 1 функции n переменных будет равно 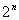 , т.е. для функции одной переменной -
, т.е. для функции одной переменной - 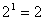 , двух -
, двух -  , трёх -
, трёх - 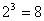 и т.д. Таким образом, таблица истинности функции одной переменной содержит 2 строки, двух – 4, трёх – 8 и т.д. При этом множество значений аргументов принято упорядочивать по лексикографическому порядку, который легко запомнить, например, используя понятие дерева из теории графов. На каждом этаже этого дерева расположены всевозможные наборы
и т.д. Таким образом, таблица истинности функции одной переменной содержит 2 строки, двух – 4, трёх – 8 и т.д. При этом множество значений аргументов принято упорядочивать по лексикографическому порядку, который легко запомнить, например, используя понятие дерева из теории графов. На каждом этаже этого дерева расположены всевозможные наборы 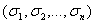 0 и 1 длины n: на первом – n=1, на втором – n=2, на третьем - n=3 и т.д. (см. рисунок 2.2.3);
0 и 1 длины n: на первом – n=1, на втором – n=2, на третьем - n=3 и т.д. (см. рисунок 2.2.3);
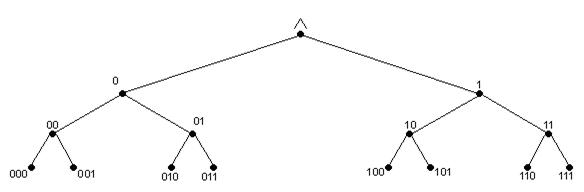
Рисунок 2.2.3
б) задание функций перечислением всех наборов, на которых 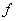 принимает значение 0 (нулевые наборы) и всех наборов, на которых она принимает значение 1 (единичные наборы);
принимает значение 0 (нулевые наборы) и всех наборов, на которых она принимает значение 1 (единичные наборы);
в) задание функции формулой;
г) задание с помощью вектора значений. Вектором значений функции 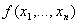 называется упорядоченный набор всех значений
называется упорядоченный набор всех значений 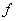 , при котором все значения упорядочены по лексикографическому порядку множества аргументов
, при котором все значения упорядочены по лексикографическому порядку множества аргументов  .
.
Рассмотрим на примере эти способы задания функции.
Пример 2.2.1 - Имеется устройство, фиксирующее принятие некоторой резолюции тремя персонами (комитетом трёх). Каждый член комитета при одобрении резолюции нажимает свою кнопку. Если большинство членов согласны, то резолюция принята, что фиксирует устройство. Таким образом, устройство реализует функцию 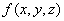 , таблица истинности которой имеет вид:
, таблица истинности которой имеет вид:
Т а б л и ц а 2.2.1
| x | y | z | 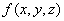
|
Зададим эту функцию нулевыми и единичными наборами:  - нулевые наборы;
- нулевые наборы; 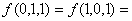
 - единичные наборы. Если задавать эту функцию с помощью вектора значений, то это будет набор (00010111).
- единичные наборы. Если задавать эту функцию с помощью вектора значений, то это будет набор (00010111).
Иногда применяют и другие способы задания функций (см., например, [3], стр.124 или [9], стр.124).
Итак, число всех наборов 0 и 1 для функции n переменных равно 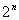 . Число же всех возможных различных функций n переменных равно числу всех возможных расстановок 0 и 1 в столбце с
. Число же всех возможных различных функций n переменных равно числу всех возможных расстановок 0 и 1 в столбце с 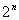 строками, т.е. равно
строками, т.е. равно  . Значит, если
. Значит, если  - множество всех значений аргументов функции
- множество всех значений аргументов функции 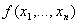 , а
, а  - множество всех функций от
- множество всех функций от 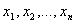 , то мощности этих множеств будут
, то мощности этих множеств будут  . Таким образом,
. Таким образом,  растёт очень быстро:
растёт очень быстро: 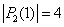 ,
, 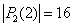 ,
, 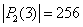 и т.д.
и т.д.
Особую роль в алгебре логики играют функции одной и двух переменных. Например, множество всех логических функций одной переменной 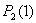 состоит из четырёх функций, которые можно представить их таблицей истинности.
состоит из четырёх функций, которые можно представить их таблицей истинности.
Т а б л и ц а 2.2.2
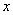
| 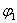
| 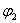
| 
| 
|
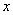
| 
|
Функции 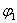 и
и  константы 0 и 1,
константы 0 и 1, 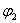 =х – повторяет переменную х, (т.е. значения этих функций не зависят от переменной х, поэтому говорят, что переменная х не существенна или фиктивна для этих функций). Наибольший интерес представляет функция
=х – повторяет переменную х, (т.е. значения этих функций не зависят от переменной х, поэтому говорят, что переменная х не существенна или фиктивна для этих функций). Наибольший интерес представляет функция  =
=  - унарная операция отрицания. Аналогичным образом можно построить таблицу истинности для всех 16 (
- унарная операция отрицания. Аналогичным образом можно построить таблицу истинности для всех 16 (  ) функций двух переменных. Среди них 7 логических операций (конъюнкция, дизъюнкция, и т.д.), остальные не представляют интереса. Заметим, что функция может быть представлена как операция, если её значения лежат в области определения этой функции. В этом смысле все функции математической логики могут быть представлены операциями.
) функций двух переменных. Среди них 7 логических операций (конъюнкция, дизъюнкция, и т.д.), остальные не представляют интереса. Заметим, что функция может быть представлена как операция, если её значения лежат в области определения этой функции. В этом смысле все функции математической логики могут быть представлены операциями.
Логические функции трёх и более переменных обычно задаются либо таблицей истинности, либо формулой, состоящей из знаков переменных и знаков унарных и бинарных операций. В общем случае формула описывает логическую функцию как суперпозицию других, более простых функций.
Определение.Функцию 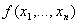 называют суперпозицией функций
называют суперпозицией функций 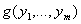 и
и  ,
, 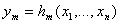 , е сли
, е сли 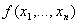 =. =
=. =  .
.
Пример 2.2.2 - Функция  есть суперпозиция
есть суперпозиция  и
и 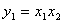 ,
,  ,
,  .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 605; Нарушение авторских прав?; Мы поможем в написании вашей работы!