Дизъюнктивные и конъюнктивные нормальные формы

Базис 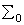= 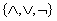наиболее изучен и имеет самое широкое применение на практике.

Определение.Элементарной конъюнкцией (дизъюнкцией) называется конъюнкция (дизъюнкция) переменных или их отрицаний.

Пример 2.3.1 –

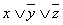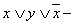а) и элементарные дизъюнкции;

б) 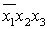и элементарные конъюнкции;

в) 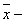одновременно является и элементарной дизъюнкцией и элементарной конъюнкцией.

Определение.Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций. Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций.

Пример 2.3.2 –

а) 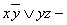ДНФ;

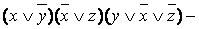б) КНФ.

Теорема.Любая формула может быть приведена к ДНФ (КНФ) (т.е. любая формула эквивалентна некоторой ДНФ (КНФ)).

Правило приведения формулы к ДНФ:

а) все логические операции, присутствующие в формуле, выразить через 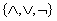, используя эквивалентности:

1) ;

2) ;

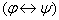
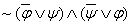
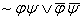3) ;

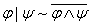4) ;

5) ;

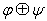
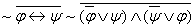б) перенести все отрицания к переменным по закону де Моргана:

;

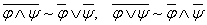в) используя закон дистрибутивности, преобразовать формулы так, чтобы все конъюнкции выполнялись раньше дизъюнкций: .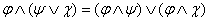

Пример 2.3.3 - Приведём к ДНФ формулу 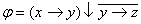. Для этого

заменим на , затем применим закон де Моргана и закон двойного отрицания: = .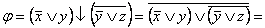

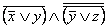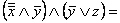
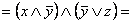
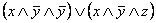Заметим, что последняя формула в примере в некоторых учебниках уже считается ДНФ, в других же считают, что в элементарных конъюнкциях и дизъюнкциях каждая переменная должна встречаться не более одного раза. Для удаления лишних переменных применяют следующие эквивалентности:

а) 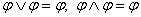(закон идемпотентности);

б) 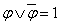(закон исключённого третьего), 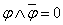(закон противоречия); в) 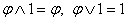, 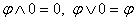- (свойства констант).

Поэтому, используя закон идемпотентности, в последнем примере получим ДНФ: .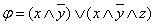

Приведение формулы к КНФ производится так же как к ДНФ, только вместо пункта в) применяется пункт в :

в 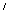) используя закон дистрибутивности, преобразовать формулы так, чтобы все дизъюнкции выполнялись раньше конъюнкций, т.е. .

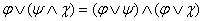Пример 2.3.4 - Приведём к КНФ формулу .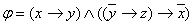

Заменим операцию 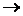, используя формулу :

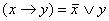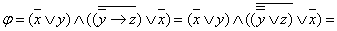[закон де Моргана, двойное

отрицание] 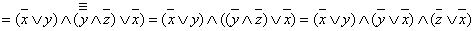- КНФ.

ДНФ и КНФ имеют тот недостаток, что они не обладают свойством единственности, т.е. одна и та же формула имеет несколько ДНФ и КНФ. Этим недостатком не обладают совершенные нормальные формы.

Определение.Совершенной дизъюнктивной нормальной формой(СДНФ) называется ДНФ, в которой в каждую элементарную конъюнкцию каждая переменная входит ровно один раз, причём, входит либо сама переменная, либо её отрицание, и среди элементарных конъюнкций не должно быть одинаковых; совершенной конъюнктивной нормальной формой(СКНФ) называется КНФ, в которой в каждую элементарную дизъюнкцию каждая переменная входит ровно один раз, причём, входит либо сама переменная, либо её отрицание, и среди элементарных дизъюнкций не должно быть одинаковых.

Пример 2.3.5 –

а) 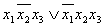- СДНФ;

б) 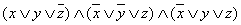- СКНФ;

в) 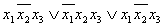- не СДНФ, т.к. содержит две одинаковых элементарных конъюнкции;

г) 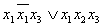- не СДНФ, т.к. в одной элементарной конъюнкции содержится и переменная и её отрицание: .

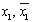Теорема.(Существование и единственность СДНФ и СКНФ). Всякая логическая формула единственным образом (с точностью до порядка следования элементарных конъюнкций (дизъюнкций)) может быть представлена в СДНФ (СКНФ).

Для приведения формулы к СДНФ можно использовать один из двух методов:

І метод: приводим формулу к ДНФ; если какая-то элементарная конъюнкция не содержит некоторой переменной у, то добавляем её, используя закон расщепления: 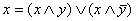; убираем одинаковые элементарные конъюнкции, используя закон идемпотентности .

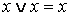Пример 2.3.6 - Получим СДНФ функции 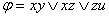, заданной в ДНФ:

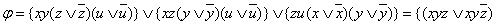
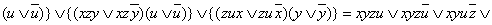
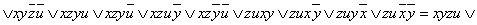
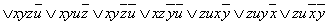- СДНФ.

ІІ метод:для данной формулы строим таблицу истинности, потом применяем правило, основанное на теореме Шеннона: СДНФ функции 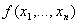содержит столько элементарных конъюнкций, сколько единиц в столбце значений 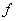; каждому единичному набору нулей и единиц 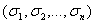соответствует элементарная конъюнкция всех переменных, в которой 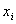взято с отрицанием, если 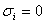и без отрицания, если .

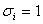Пример 2.3.7 - Для функции 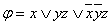, заданной в ДНФ, найти СДНФ. Построим таблицу истинности:

Т а б л и ц а 2.3.1

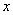
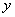
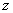
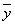
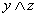
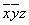
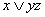
Функция принимает значение 1 при следующих значениях аргументов: 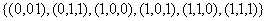- это её единичные наборы. По выше приведённому правилу, 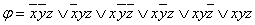- СДНФ.

Приведение формулы к СКНФ аналогично приведению к СДНФ. Также существует два метода:

а) метод элементарных преобразований;

б) СКНФ находят по таблице истинности: СКНФ функции 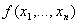содержит столько элементарных дизъюнкций, сколько нулей в столбце значений 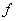; каждому нулевому набору нулей и единиц 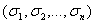соответствует элементарная дизъюнкция всех переменных, в которой 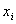взято с отрицанием, если 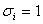и без отрицания, если .

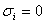Пример 2.3.8 - Рассмотрим функцию из предыдущего примера 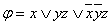. Приведём её к СКНФ двумя способами:

а)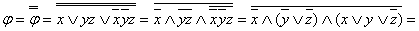

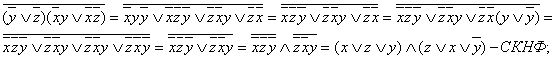
б) из таблицы истинности выпишем нулевые наборы: 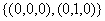, значит, по выше приведённому правилу, 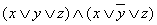- СКНФ.

Минимизация булевых функций в классе ДНФ. Карты Карно

При решении практических задач часто возникает проблема минимизации логических формул, в смысле, например, найти формулу, содержащую наименьшее число переменных, или наименьшее число операций, или наименьшее количество подформул определённого вида и т.д. К настоящему времени наиболее изучена задача отыскания дизъюнктивных форм, минимальных по числу вхождений переменных. Под вхождением переменной понимается место, которое переменная занимает в формуле.

Определение.Минимальной ДНФ (МДНФ) называется ДНФ с наименьшим числом вхождений переменных.

Существует много способов отыскания МДНФ (метод Квайна, неопределённых коэффициентов, с помощью гиперкубов и т.д.). Остановимся на наиболее простом – с использованием карт (диаграмм) Карно.

Карта Карно– это таблица, каждая клетка (ячейка) которой соответствует некоторой элементарной конъюнкции всех переменных. Для функции n переменных 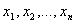существует 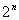возможных комбинаций их значений, состоящих из 0 и 1. То есть, например, для n=2 имеем элементарные конъюнкции 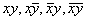, которым соответствуют следующие наборы 0 и 1: (1,1), (1,0), (0,1), (0,0); для n=3 - 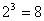- - 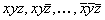(1,1,1), (1,1,0),…,(0,0,0) и т.д. Карты Карно строятся в виде таблицы размером 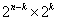так, что её столбцы соответствуют значениям переменных , строки - 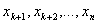(или наоборот); вообще, для одной и той же функции может быть построено несколько карт, важно, чтобы соседние ячейки (как по вертикали, так и по горизонтали) отличались только значением одной переменной.

Мы будем рассматривать в основном функции двух, трёх и четырёх переменных. Для них карты Карно имеют следующий вид:

а) для функции двух переменных х, у - рисунок 2.3.1;

б)для функции трёх переменных 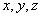- рисунок 2.3.2;

в) для функции четырёх переменных 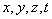- рисунок 2.3.3.

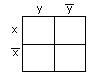
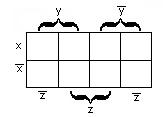
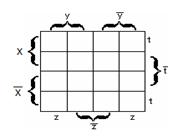
Рисунок 2.3.1 Рисунок 2.3.2 Рисунок 2.3.3

Для определения МДНФ булевой функции, сначала надо найти её СДНФ, затем каждую элементарную конъюнкцию СДНФ отметить единицей в соответствующей ячейке карты Карно.

Пример 2.3.9 - Функци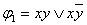и и 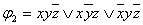заданы в форме СДНФ. Карта Карно для на рисунке 2.3.4; для - на рисунке 2.3.5.

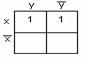
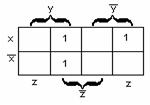
Рисунок 2.3.4 Рисунок 2.3.5

Заметим, что, если в картах Карно две, четыре, восемь (для функции четырёх переменных) соседних ячеек по вертикали или по горизонтали содержат 1, то эти ячейки объединяют в блоки (на картах их отмечают овалами) и соответствующие этим блокам дизъюнкции элементарных конъюнкций можно упростить. Так, в примере 2.3.9 для функции 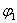имеем блок из двух ячеек, на рисунке он отмечен овалом. Этому блоку соответствует дизъюнкция 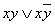, упрощая которую, получим: 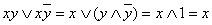. Таким образом, блоку из двух ячеек функции двух переменных отвечает одна переменная х, а именно та переменная, которая полностью «покрывает» этот блок. Формула упростилась .

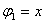Для функции 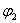также имеем один блок из двух ячеек, ему соответствует дизъюнкция элементарных конъюнкций 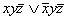, упрощая которую получим 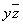, т.е. блоку из двух ячеек функции трёх переменных соответствует конъюнкция двух переменных, «покрывающих» этот блок. Формула упростилась .

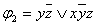Рассмотрим ещё несколько примеров.

Пример 2.3.10 - 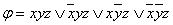- СДНФ функции. Её карта Карно на рисунке 2.3.6. Так как z находится на обоих концах карты, то её (карту) можно «скрутить» и считать, что 1 в углах карты образуют блок из четырёх ячеек. Эти четыре ячейки полностью «покрывает» переменная z, т.о., МДНФ функции будет .

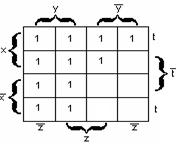
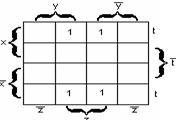
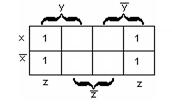
Рисунок 2.3.6 Рисунок 2.3.7 Рисунок 2.3.8

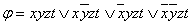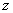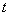Пример 2.3.11 - - СДНФ функции. Её карта Карно на рисунке 2.3.7. На карте есть блок из четырёх ячеек, который покрывают переменные и , поэтому МДНФ функции будет: .

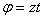Пример 2.3.12 - Карта Карно для функции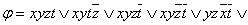

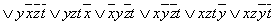заданной в СДНФ на рисунке 2.3.8.

На карте имеем: блок из 8 ячеек покрывает переменная y; двум блокам из 4 ячеек соответствуют элементарные конъюнкци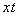и и 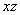, поэтому МДНФ будет: .

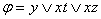Дата добавления: 2014-12-27