Основные понятия и определения. Элементы теории графов

Элементы теории графов

Графы – это один из способов наглядного представления взаимосвязей между различными объектами. На языке теории графов формулируются и решаются многие задачи сетевого планирования и управления – сети железных дорог, телефонные и комьютерные сети, ирригационные системы; эта теория позволяет формализовать, анализировать и решать задачи экономической и производственной практики, производить анализ и синтез функциональных блоков комьютеров, комплексов программ и т.д.

Графы описывают связи между объектами, а связи могут быть «направленными» (например, в генеалогическом дереве) или «ненаправленными» (например, сеть дорог с двусторонним движением). Поэтому в теории графов выделяют два основных типа графов: ориентированные (орграф) и неориентированные (неорграф, н-граф). Иногда рассматривают графы смешанного типа.

Определение.Графом G называется совокупность двух множеств: V – вершин и E – рёбер (для н-графа) или дуг (для орграфа). Обозначается G=G(V,E) или G=(V,E).

Пусть - множество вершин. Тогда для н-графа 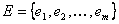, где ребра 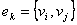- двухэлементные подмножества множества V; для орграфа 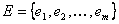, где дуги 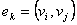- упорядоченные пары, т.е. .

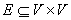Если - ребро ( 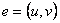- дуга), то вершины и называются концами ребра ( - началом, - концом дуги); вершины и называются инцидентными ребру (дуге) , а ребро (дуга) инцидентным(ой) вершинам и ; вершины и называются смежными,если они являются концами одного ребра (дуги).

Ребро (дуга), концевые вершины которого совпадают, называется петлёй. Рёбра (дуги) инцидентные одной и той же паре вершин, называются параллельными или кратными. Граф, содержащий кратные рёбра (дуги), называется мультиграфом. Граф называется конечным, если множетва V и E конечны, пустым – если множество его вершин V (а значит и рёбер) пусто. Некоторые вершины могут не войти в список пар множества E, они называются изолированными. Граф, у которого все вершины изолированные, называется нуль-графом; антиподом нуль-графа является полный граф: его рёбрами являются все возможные пары его вершин (у него нет петель и кратных рёбер).

Заметим, что многие теоремы и определения в теории графов могут быть отнесены как к н-графам, так и к орграфам. Часто, когда совершенно ясно, о каком типе графов идёт речь, рёбра, как и дуги, обозначают круглыми скобками, т.е. вместо записывают 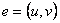. Каждому н-графу канонически соответствует орграф с тем же множеством вершин, в котором каждое ребро заменено двумя дугами, инцидентными тем же вершинам и имеющими противоположные направления.

Определение.Степенью (иногда валентностью) вершины (обозначается 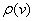или d( )) называется количество всех инцидентных ей рёбер.

Если m – число рёбер н-графа G, то =2m. Предполагается, что петля даёт вклад 2 в степень вершины. Для вершин орграфа определяются также две локальные степени.

Определение.Степенью выхода вершины (обозначается , ) называется число дуг с началом в вершине ; степенью входа вершины (обозначается , ) - число дуг с концом в вершине ; 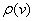= + . Если m – число дуг орграфа G, то = =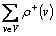m, причём петля даёт вклад 1 в обе степени.

Дата добавления: 2014-12-27