Понятие о мощности множеств

Часто возникает необходимость сравнивать множества по числу элементов. В этом случае возникает понятие мощности множества.

Определение.Множества А и В называются эквивалентными (обозначается А~В) если существует биекция f: А 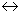В (т.е. между ними можно установить взаимно однозначное соответствие (в.о.с.)).

Очевидно, что два конечных множества эквивалентны тогда и только тогда, когда они имеют одинаковое число элементов. Если два множества бесконечны и между ними можно установить в.о.с., то они обладают также чем-то общим, что мы будем называть мощностью. Итак, любые два эквивалентных множества (конечные или бесконечные) имеют одинаковую мощность или являются равномощными. Или более точное определение.

Определение. Мощностью множества А называется класс всех множеств, эквивалентных множеству А (мощность обозначается ).

Имеется три возможности:

а) если А - конечное множество, имеет n элементов, то = n;

б) если А - бесконечное множество и эквивалентно множеству натуральных чисел N, то А называют счётным множеством, записывают = . Таким образом, у счётного множества все элементы можно пронумеровать;

в) существуют бесконечные множества, которые нельзя привести во в.о.с. с множеством натуральных чисел. Например, установлено, что множество всех действительных чисел отрезка [0,1] не является счётным (теорема Кантора). Принято мощность этого множества называть континуум (часто обозначается с), а множества такой мощности континуальными.

Доказано, что если А континуальное множество, то 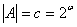, т.е. мощность континуума равна мощности множества всех подмножеств счётного множества. Вообще, для любого множества А: Р(А) 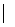= , где Р(А) – булеан.

Примеры счётных множеств:

а) множество целых чисел Z, а также ;

б) множество рациональных чисел Q;

в) любое бесконечное подмножество множества N, например, {2,4,6,8,…};

г) (вообще ).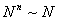

Примеры континуальных множеств:

а) множество всех действительных чисел R или множество точек числовой оси;

б) множество всех точек плоскости (пространства) ;

в) множество всех подмножеств счётного множества (т.е. булеан счётного множества).

Как показано в теории множеств, для множества любой мощности множество его подмножеств имеет более высокую мощность. Поэтому не существует множества максимальной мощности. На мощность множеств можно смотреть как на новый объект, называемый кардинальным числом или кардиналом. Примерами кардиналов могут быть:

а) любое натуральное число (как мощность конечного множества);

б) и т.д.

Отметим, что существование биекции между двумя множествами позволяет перенести изучение свойств с одного множества на другое, что многое упрощает, например, некоторые свойства конечного множества А, = n можно изучать по множеству {0,1,2,3,…n-1}.

Дата добавления: 2014-12-27